Проверка гипотезы о нормальности распределения полученных результатов наблюдений
Нормальный закон распределения, называемый часто распределением Гаусса описывается зависимостью
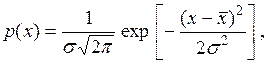 (23)
(23)
где σ – параметр рассеивания распределения, равный среднему квадратическому отклонению.
Широкое использование нормального распределения на практике объясняется теоремой теории вероятностей, утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.
При количестве измерений n<10 проверить гипотезу о виде распределения результатов измерения невозможно.
При числе данных 10<n<50 также трудно судить о виде распределения. Поэтому для проверки соответствия распределения данных нормальному распределению используют составной критерий. Если гипотеза о нормальности отвергается хотя бы по одному из критериев, считают, что распределение результатов измерения отлично от нормального.
Критерий 1. Вычисляется значение d по формуле
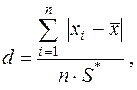 (24)
(24)
где S* – смещенное СКО;
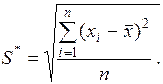 (25)
(25)
Гипотеза о нормальности подтверждается, если
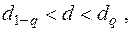 (26)
(26)
где 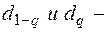 процентные точки распределения значений d, которые находятся по табл. 21.
процентные точки распределения значений d, которые находятся по табл. 21.
Таблица 21
Значения процентных точек q для распределения d
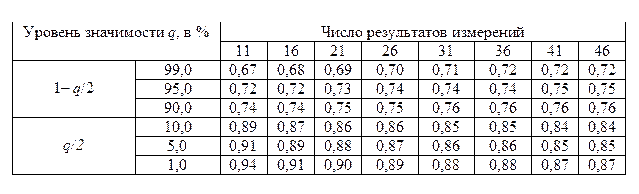
Критерий 2. Гипотеза о нормальности распределения результатов измерения подтверждается, если не более m разностей 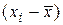 превзошли значения S×zp/2. Здесь:
превзошли значения S×zp/2. Здесь:
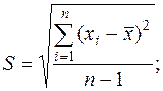 (27)
(27)
zp/2 – верхняя 100 P/2 – процентная точка нормированной функции Лапласа.
Значения доверительной вероятности P выбираются из табл. 22.
Пример
В табл. 23 приведены результаты измерения угла одним оператором, одним и тем же теодолитом, в одних и тех же условиях. Проверить, можно ли считать, что приведенные в табл. 23 данные принадлежат совокупности, распределенной нормально.
Таблица 22
Значения доверительной вероятности Р
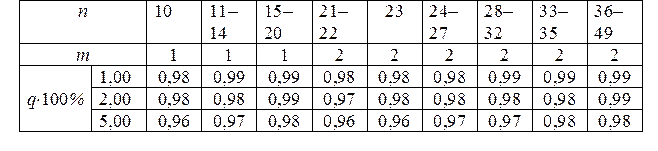
Таблица 23
Дата добавления: 2016-06-18; просмотров: 6333;











