Уравнения напряжения и характеристики синхронных генераторов
Напряжение фазы на зажимах генератора определяется суммарной намагничивающей силой индуктируемой в этой обмотке за вычетом падения напряжения на активном сопротивлении фазы, то есть:
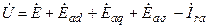 . .
| (5.2.1) |
Э.д.с. реакции якоря и рассеяние можно выразить через соответствующие индуктивные сопротивления:
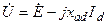 , ,
| (5.2.2) |
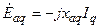 , ,
| (5.2.3) |
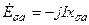 , ,
| (5.2.4) |
Тогда уравнение примет вид:
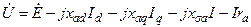 , ,
| (5.2.5) |
Его можно прочитать:
Напряжение генератора U равно э.д.с., индуктируемой потоком возбуждения минус падение напряжения в индуктивных сопротивлениях реакции якоря, индуктивном сопротивлении рассеяния и активном сопротивлении якоря.
Большинство свойств СГ можно оценить по его характеристикам, определяющим зависимость между I, U и if при постоянстве cos φ, n1 или f в установившемся симметричном режиме при различных значениях нагрузки, которые строятся в о.е.
Характеристики могут быть или построены теоретически или сняты опытным путём. Обычно для опытного снятия характеристик СГ используют универсальную схему:
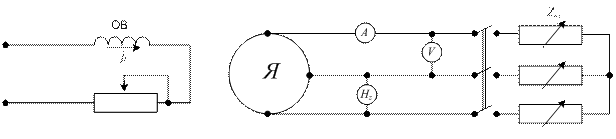
Рисунок 5.2.1 – Электрическая схема для снятия характеристик СГ
Характеристика холостого хода
Это зависимость между 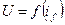 , при I=0 (Zнг=∞); f1=const; т.е. U=E.
, при I=0 (Zнг=∞); f1=const; т.е. U=E.
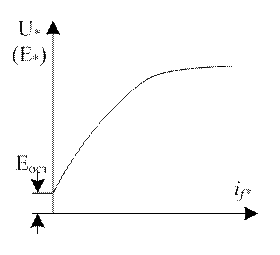
Рисунок 5.2.2 – Характеристика холостого хода СГ
Начинают снятие х.х.х. с точки, соответствующей э.д.с. от остаточного потока.
Характеристика х.х. может быть получена из расчёта магнитной цепи машины, выполненному для отдельных участков.
При отсутствии возможности снятия характеристики х.х. и для упрощения расчётов используют так называемые нормальные характеристики (в о.е. соответствующие средним данным турбо и гидрогенераторов).
Характеристика короткого замыкания.
Это зависимость 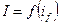 ;
; 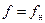 ; U=0.
; U=0.
Если положить, что ra=0, то сопротивление в якорной цепи чисто индуктивное, т.е. ψ=900, а I=Id (Iq=0).
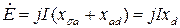 . .
| (5.2.6) |
Реакция якоря – чисто размагничивающая, причём э.д.с. от результирующего потока зазора:
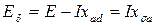
| (5.2.7) |
очень мала, 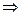 Фδ тоже мал и машина ненасыщенна, поэтому характеристика к.з. прямолинейна. Характеристику к.з. можно рассчитать как
Фδ тоже мал и машина ненасыщенна, поэтому характеристика к.з. прямолинейна. Характеристику к.з. можно рассчитать как 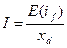 .
.
Зная характеристики х.х. и к.з. можно рассчитать синхронное продольное значение xd и xd∞ для любого if, в том числе и номинального:
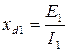 , ,
| (5.2.8) |
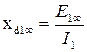 . .
| (5.2.9) |
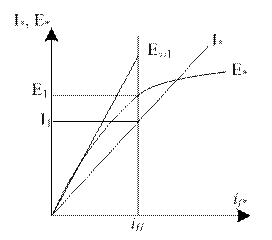
Рисунок 5.2.3 –Насыщенные характеристики холостого хода
Важным показателем СГ является отношение короткого замыкания k0к.з.
Согласно ГОСТу
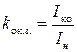 , ,
| (5.2.10) |
где Iко – это ток к.з. соответствующий такому if0 , который в режиме х.х. даёт E = Uн,
т.е.
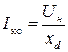 , ,
| (5.2.11) |
xd – соответствует Eδ = Uн.
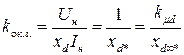 . .
| (5.2.12) |
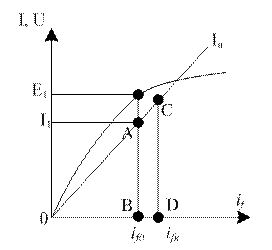
Рисунок 5.2.4 –Определение отношения короткого замыкания
Т.е. о.к.з. равно обратному продольному сопротивлению в о.е.. Если xd*>1, тот Iко<Iн, относительно не большое значение Iк определяется сильным размагничивающим действием реакции якоря.
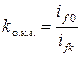 ; (из подобия треугольников ОАВ и ОСD):
; (из подобия треугольников ОАВ и ОСD):
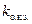 тем больше, чем больше зазор δ.
тем больше, чем больше зазор δ.
Обычно у гидрогенераторов 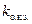 =0,8
=0,8  1,8 у турбогенераторов – 0,4
1,8 у турбогенераторов – 0,4  1,0.
1,0.
Внешняя характеристика.
Это зависимость U=f(I), cosφ=const, f1=fн, if=const.
Внешнюю характеристику снимают для двух режимов: понижения и повышения напряжения. В первом случае начинают с режима холостого хода, когда U=Uн, затем вводят нагрузку до I=Iн.
Во втором случае выставляют режим Uн и Iн, а затем постепенно сбрасывают нагрузку до 0.
Наиболее интересен второй режим, т.к. он позволяет определить номинальноеизменениенапряженияСГ – это изменение напряжения на зажимах СГ при уменьшении тока нагрузки от номинального значения до 0.
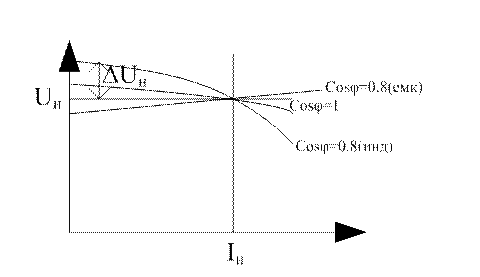
Рисунок 5.2.5 – Внешняя характеристика СГ
Синхронные генераторы обычно рассчитываются для работы с активно-индуктивной нагрузкой и cosφ = 0,8.
ΔUн выражается обычно в % (25  35%), но не ГОСТируется как в трансформаторах. У турбогенераторов ΔUн больше, чем у гидрогенератора, т.к. они имеют больше xd*.
35%), но не ГОСТируется как в трансформаторах. У турбогенераторов ΔUн больше, чем у гидрогенератора, т.к. они имеют больше xd*.
Характер внешней характеристики зависит от характера нагрузки. Если cosφ – активно-индуктивная, то из-за размагничивающего действия реакции якоря U с ростом I падает.
При ёмкостном токе реакции якоря – намагничивающая, т.е. она увеличивает E с ростом I (и, следовательно и U).
Регулировочная характеристика.
Это зависимость if = f(I) при f1 = fном, U = Uном cosφ = const, которая показывает, как нужно регулировать ток возбуждения СГ, чтобы при изменении нагрузки его напряжение оставалось неизменным.

Рисунок 5.2.6 – Регулировочная характеристика СГ
Вид регулировочной характеристики также зависит от характера нагрузки., и соответственно реакции якоря. При отстающем токе продольная реакция якоря является размагничивающей и для компенсации ее влияния на поток Фδ и напряжение U необходимо при увеличении тока I увеличивать ток возбуждения. В случае чисто активной нагрузки, if также надо увеличивать с ростом I, поскольку растёт падение напряжения в ra и xσa, но размагничивающая реакция якоря при этом слабее. При емкостной нагрузке требуется уменьшение тока возбуждения (намагничивающая реакция якоря).
Нагрузочная характеристика.
Это зависимость U = f( 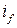 ) при I = const, cosφ = const и f1 = fном, т.е. х.х.х. – это частный случай нагрузочной характеристики, когда I = 0.
) при I = const, cosφ = const и f1 = fном, т.е. х.х.х. – это частный случай нагрузочной характеристики, когда I = 0.
Практический интерес представляет индуктивная нагрузочная характеристика, которая соответствует чисто индуктивной нагрузке СГ (cosφ=0).
Из векторной диаграммы видно, что 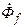 и
и 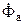 здесь складываются алгебраически, а
здесь складываются алгебраически, а 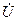 и
и 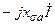 (
( 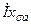 ) – арифметически.
) – арифметически.
При этом I=Iн. Если положить, что ra =0, то векторная диаграмма будет иметь вид:
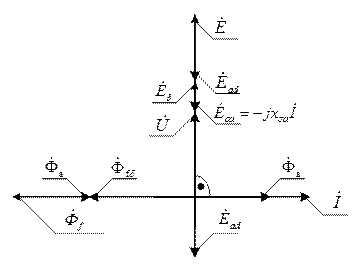
Рисунок 5.2.7 – Векторная диаграмма СГ в режиме индукционной характеристики
По характеристикам х.х. и индукционной нагрузочной, можно построить реактивныйтреугольник, вертикальный катет которого СВ равен падению напряжения в
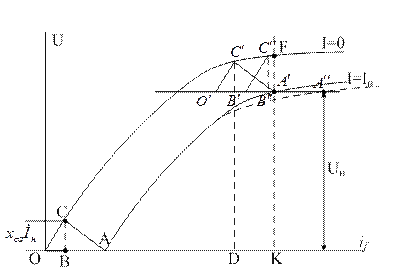
Рисунок 5.2.8 – Построение реактивного треугольника
сопротивлении рассеяния Iнxσa, а горизонтальный АВ равен н.с. реакции якоря в масштабе тока if, или kidIн.
Этот треугольник можно построить, если известны:
1) сопротивление рассеяния 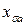 ;
;
2) прямолинейная часть характеристики х.х.;
3) OA =ifк – ток возбуждения при коротком замыкании, Iк = Iн, U=0, т.е. для точки А уравнение СГ:
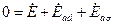 ; (ra=0) ; (ra=0)
| (5.2.13) |
Поскольку все три э.д.с. совпадают по фазе, то можно перейти к алгебре:
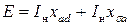 , ,
| (5.2.14) |
т.е. при коротком замыкании ОА часть н.с. идёт на 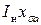 (ОВ), а остаток – на
(ОВ), а остаток – на 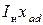 .
.
Если известно 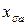 , то можно по х.х.х. найти if, необходимый для компенсации
, то можно по х.х.х. найти if, необходимый для компенсации 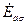 (ОВ). Следовательно АВ = ОА–ОВ – в масштабе if – н.с. р.я..
(ОВ). Следовательно АВ = ОА–ОВ – в масштабе if – н.с. р.я..
Поскольку 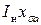 и
и 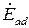 практически не зависят от
практически не зависят от 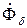 , то индуктивную нагрузочную характеристику можно построить по х.х.х., передвигая треугольник ОСА параллельно, причём точка С должна скользить по х.х.х..
, то индуктивную нагрузочную характеристику можно построить по х.х.х., передвигая треугольник ОСА параллельно, причём точка С должна скользить по х.х.х..
Для точки 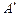 ОК должна индуктировать
ОК должна индуктировать 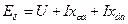 . DK индуктирует
. DK индуктирует 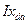 ; OD -
; OD - 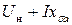 (
( 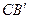 ) – что и требовалось доказать.
) – что и требовалось доказать.
По двум характеристикам можно найти xσa.
Из точки 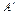 отложить
отложить 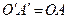 , затем
, затем 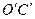 параллельно ОС (найти точку
параллельно ОС (найти точку 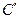 ), потом
), потом
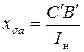 , ,
| (5.2.15) |
кроме того, можно найти:
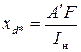 . .
| (5.2.16) |
Индуктивное сопротивление Потье.
Согласно опыту, индуктивная характеристика не совсем совпадает с построенной описанным способом, а уходит несколько вправо. Это объясняется тем, что хотя для точек 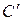 и
и 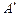
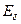 и
и 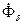 одинаковы, но н.с. разные, и поток рассеяния (для ОК) больше, насыщения полюса и следовательно
одинаковы, но н.с. разные, и поток рассеяния (для ОК) больше, насыщения полюса и следовательно 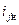 надо несколько увеличить на величину
надо несколько увеличить на величину 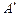
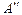 .
.
В этом случае сопротивление рассеяния будет несколько большим:
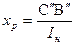 ; ;
| (5.2.17) |
- индуктивное сопротивление Потье или расчётное индуктивное сопротивление рассеяния ОЯ:
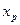 =(1,05 =(1,05 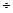 1,3)xσa. 1,3)xσa.
| (5.2.18) |
| <== предыдущая лекция | | | следующая лекция ==> |
| Работа автономного синхронного генератора при симметричной нагрузке | | | Векторные диаграммы синхронного генератора |
Дата добавления: 2016-06-18; просмотров: 3013;











