Работа автономного синхронного генератора при симметричной нагрузке
5.1 Магнитное поле и параметры обмотки якоря
Собственное магнитное поле, создаваемое обмоткой статора (якоря) синхронной машины, называется полем реакции якоря. Поток реакции якоря обозначается как Фа, в зависимости от характера нагрузки этот поток может складываться или вычитаться с Фf (намагничивать или размагничивать машину), может искажать поток возбуждения, наводить э.д.с. в обмотки якоря.
Поэтому реакция якоря оказывает весьма значительное влияние на характеристики и поведение синхронной машины в установившихся и переходных режимах.
Наиболее сложный характер реакциz якоря имеет в явнополюсной машине, поскольку ротор такой машины обладает магнитной несимметрией. Поток возбуждения всегда действует вдоль оси полюсов (продольная ось - d), поэтому магнитное сопротивление для него – величина постоянная.
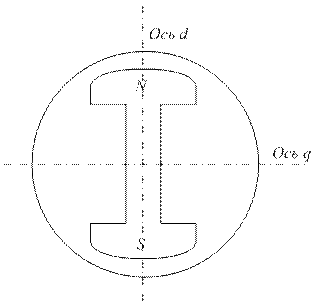
Рисунок 5.1.1 –Магнитопровод СМ с магнитной несимметрией
Однако поток реакции якоря может действовать и вдоль поперечной оси q (междуполюсной). Ввиду этой несимметрии возникает необходимость рассматривать действие реакции якоря отдельного по продольной и поперечной осям. Метод был предложен А. Блонделем в 1895г. и называется методом (теорий) двух реакций. Метод основан на принципе наложения, что не вполне корректно, но тем не менее он широко применяется особенно для анализа переходных процессов синхронных машин.
Рассмотрим влияние характера нагрузки на характер реакции якоря.
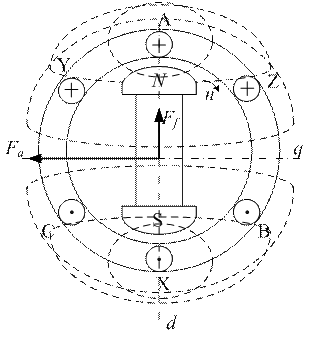
Рисунок 5.1.2 –Реакция якоря при чисто активной нагрузке
Если ψ=0 (угол между 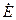 и
и 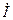 ).
).
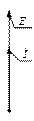
Рисунок 5.1.3 –Векторная диаграмма СГ при чисто активной нагрузке
ЭДС в проводнике а следовательно и ток АХ максимален, когда ось q совпадает с осью АХ. Поле, создаваемое АХ также вращается со скоростью n, поэтому взаиморасположение Fa и Ff неизменно друг относительно друга, р.я.- конечная . Т.к. направлена вдоль оси q. Пусть теперь ψ = 900, т.е.  отстаёт от
отстаёт от  на π/2.
на π/2.
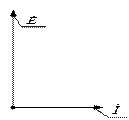
Рисунок 5.1.4 – Векторная диаграмма СГ при чисто индуктивной нагрузке
В этом случае ток достигнет своего максимума только тогда, когда полюс уже пройдёт угол α = π/2 по окружности. Н.с. р.я. будет направлена вдоль оси d в сторону, противоположную Ff , т.е. р.я. в этом случае чисто размагничивающая.
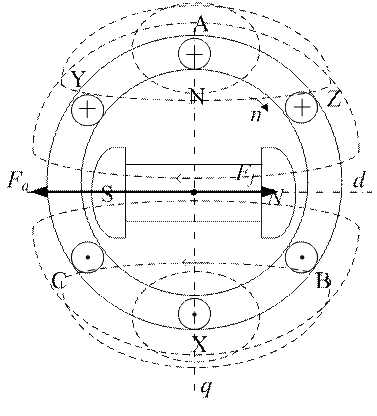
Рисунок 5.1.5 – Реакция якоря при чисто индуктивной нагрузке
Если бы ψ = 900 (опережающий ток), то р.я. была бы также продольной, но уже намагничивающей. В общем случае угол ψ может быть произвольным, а ток 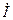 - иметь 2 составляющие:
- иметь 2 составляющие: 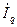 - совпадающую по фазе с
- совпадающую по фазе с 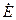 - поперечная составляющая или поперечный ток якоря, и
- поперечная составляющая или поперечный ток якоря, и 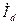 -продольную составляющее, продольный ток якоря.
-продольную составляющее, продольный ток якоря.
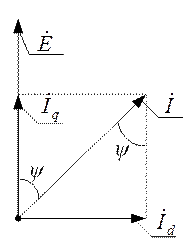
Рисунок 5.1.6 –Разложение тока якоря на продольную и поперечную составляющие
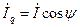 , ,
| (5.1.1) |
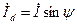 . .
| (5.1.2) |
Продольный ток создаёт продольную н.с. якоря:
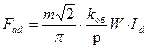 , ,
| (5.1.3) |
а поперечный – поперечную:
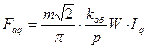 , ,
| (5.1.4) |
причём:
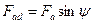 ; ; 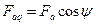
| (5.1.5) |
Максимум волны 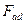 совпадает с продольной,
совпадает с продольной, 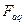 - с поперечной осью машины.
- с поперечной осью машины.
Если бы по всей окружности зазор был одинаков, то 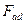 и
и 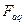 создали бы синусоидальные пространственные волны индукции с амплитудой:
создали бы синусоидальные пространственные волны индукции с амплитудой:
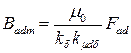 , ,
| (5.1.6) |
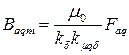 . .
| (5.1.7) |

Рисунок 5.1.7 –Кривые поля реакции якоря явнополюсной СМ по продольной и
поперечной осям
(Для разных осей коэффициенты различны). Однако из-за неравномерности 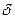 волны индукции по осям не будут синусоидальны. В теории С.М. учитываются только основные гармоники поля, причём:
волны индукции по осям не будут синусоидальны. В теории С.М. учитываются только основные гармоники поля, причём:
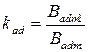 , ,
| (5.1.8) |
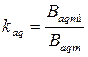 . .
| (5.1.9) |
- коэффициенты формы поля соответственно продольной и поперечной реакции якоря.
Для неявнополюсной машины kad = kaq=1.
Основные гармоники поля создают потоки продольной и поперечной реакции якоря:
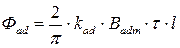 , ,
| (5.1.10) |
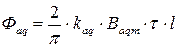 . .
| (5.1.11) |
Эти потоки вращаются синхронно с ротором и индуктируют в статоре ЭДС. самоиндукции, которая называется ЭДС продольной и поперечной реакцией якоря:
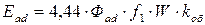 , ,
| (5.1.12) |
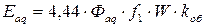 . .
| (5.1.13) |
Построим векторную диаграмму потоков и э.д.с. (временную) обмотки якоря для 0<ψ<900.
Поскольку  вместе с ротором относительно статора, то его тоже можно рассматривать как комплексную гармоническую величину.
вместе с ротором относительно статора, то его тоже можно рассматривать как комплексную гармоническую величину.
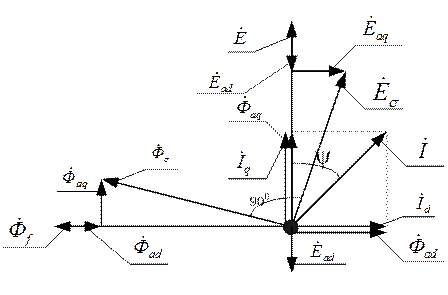
Рисунок 5.1.8 – Векторная диаграмма реакции якоря при активно-индуктивной нагрузке
Порядок построения диаграммы:
 ->
-> 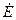 (э.д.с. взаимоиндукции ОЯ от
(э.д.с. взаимоиндукции ОЯ от 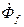 ) - >
) - > 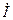 ->
-> 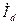 ,
, 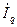 ->
-> 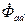 ,
, 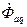 ->
-> 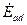 ,
, 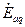 ->
-> 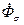 ,
, 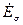 .
.
Вектор результирующего потока в воздушном зазоре определяется:
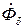 =
= 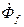 +
+ 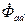 +
+ 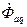 ;
;
Этот поток индуктирует в ОЯ результирующую э.д.с..
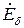 =
= 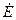 +
+ 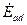 +
+ 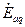 .
.
Индуктивные сопротивления реакции якоря.
ЭДС самоиндукции 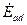 и
и 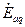 можно также представить в виде:
можно также представить в виде:
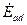 = = 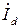 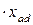 , ,
| (5.1.14) |
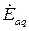 = = 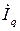 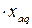 , ,
| (5.1.15) |
где 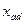 и
и 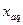 - индуктивные сопротивления продольной и поперечной реакции якоря.
- индуктивные сопротивления продольной и поперечной реакции якоря.
Если сталь сердечников ненасыщенна (µст= 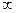 ), то kµd и kµq и значения сопротивлений будет ненасыщенными
), то kµd и kµq и значения сопротивлений будет ненасыщенными 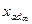 и
и 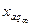 :
:
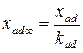 , ,
| (5.1.16) |
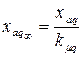 , ,
| (5.1.17) |
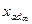 <
< 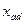 ;
; 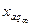 <
< 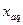 .
.
Для неявнополюсной С.М. считается, что 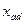 =
= 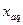 и обычно сохраняют обозначение
и обычно сохраняют обозначение 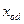 .
.
Индуктивное сопротивление рассеяния ОЯ.
Это сопротивление 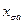 имеет составляющие: пазовую, по коронкам зубцов, лобовую, и дифференциальную, причём
имеет составляющие: пазовую, по коронкам зубцов, лобовую, и дифференциальную, причём 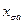 одинаково по обеим осям и практически постоянно.
одинаково по обеим осям и практически постоянно.
Таблица 5.1.1 – Индуктивные параметры синхронных машин
| Турбогенератор | Гидрогенератор | |
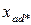
| 1,1 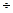 2,5 2,5
| 0,5 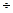 1,5 1,5
|
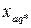
| 1,1 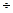 2,5 2,5
| 0,3 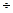 0,9 0,9
|
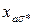
| 0,08 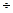 0,25 0,25
| 0,1 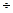 0,3 0,3
|
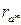
| 0,002 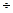 0,008 0,008
| 0,002 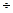 0,02 0,02
|
Поток рассеяния ОЯ 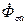 можно также разложить на составляющие:
можно также разложить на составляющие:
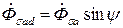 , ,
| (5.1.18) |
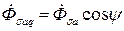 , ,
| (5.1.19) |
и считать, что 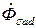 и
и 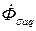 создаются соответственно токами
создаются соответственно токами 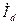 и
и 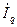 и индуктируют ЭДС.:
и индуктируют ЭДС.:
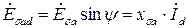 , ,
| (5.1.20) |
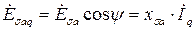 . .
| (5.1.21) |
Э.д.с. 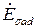 и
и 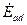 , а также
, а также 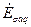 и
и 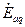 совпадают по фазе, поэтому их можно сложить попарно арифметически:
совпадают по фазе, поэтому их можно сложить попарно арифметически:
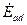 + + 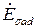 = = 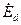 = = 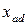 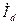 + + 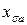 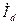 =( =( 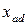 + + 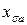 ) ) 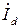 , ,
| (5.1.22) |
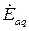 + + 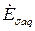 = = 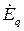 = = 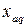 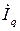 + + 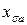 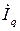 = = 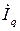 ( ( 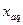 + + 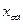 ), ),
| (5.1.23) |
где 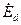 и
и 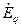 - полные э.д.с. самоиндукции якоря по продольной и поперечной осям;
- полные э.д.с. самоиндукции якоря по продольной и поперечной осям;
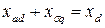 , ,
| (5.1.24) |
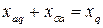 . .
| (5.1.25) |
– синхронные продольные и поперечное индуктивные сопротивления ОЯ.
Магнитные поля и параметры успокоительной обмотки.
В нормальном режиме работы успокоительная обмотка, расположенная на роторе, вращается в месте с ним с синхронной скоростью. Поэтому наведённых токов в ней нет, ибо 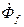 и
и 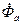 также вращаются с синхронной скоростью.
также вращаются с синхронной скоростью.
Однако в переходных режимах, а также несимметричных установившихся режимах потоки р.я. изменяются или пульсируют во времени и индуктируют в УО значительные токи.
Приведение обмоток СМ.
ОВ и ОЯ пространственно в машине распределены неодинаково, поэтому одинаковые намагничивающие силы этих обмоток создают различные по времени потоки. Однако, часто возникает необходимость анализа потоков и э.д.с. о совместного действия 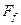 и
и 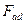 и
и 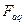 .
.
Для такого анализа надо найти ток или н.с. ОВ эквивалентные току или н.с. якоря. Т.е. привести ОЯ к ОВ. Т.е. надо, чтобы:
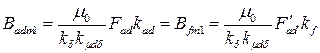 ; ;
| (5.1.26) |
тогда 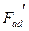 - эквивалентную (по своему действию) по своему действию н.с. р.я. по продольной оси
- эквивалентную (по своему действию) по своему действию н.с. р.я. по продольной оси 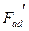 найдём из (5.1.26):
найдём из (5.1.26):
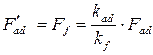 ; ;
| (5.1.27) |
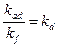 - коэффициент якоря по продольной оси. Также можно получить и
- коэффициент якоря по продольной оси. Также можно получить и 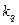 ; Коэффициента для приведения токов
; Коэффициента для приведения токов 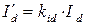 и
и 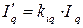 можно получить из равенства (5.1.26) при замене н.с. на соответствующие точки.
можно получить из равенства (5.1.26) при замене н.с. на соответствующие точки.
Система относительных единиц.
В теории переходных процессов синхронных машин используются о.е. При этом за единицы или базисные величины тока I, U, Z и L ОЯ принимают их номинальные значения:
Iн, Uн, Zн, и Lн;
Zн = Uн/Iн;
Lн=Zн/ω
Относительные значения:
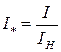 ;
; 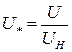 ;
; 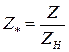 ;
; 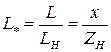 ;
; 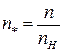 ;
;
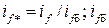 –базовый (номинальный) ток обмотки возбуждения, обеспечивающий при х.х. генератора номинальное напряжение U.
–базовый (номинальный) ток обмотки возбуждения, обеспечивающий при х.х. генератора номинальное напряжение U.
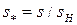 ;
;
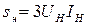 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Н.с. фазы – это сумма неподвижных в пространстве и пульсирующих во времени гармоник. | | | Уравнения напряжения и характеристики синхронных генераторов |
Дата добавления: 2016-06-18; просмотров: 1875;











