Н.с. фазы – это сумма неподвижных в пространстве и пульсирующих во времени гармоник.
Высшие гармоники н.с., также, как и ЭДС вызывают в машине ряд нежелательных явлений: добавочные потери активной мощности; добавочные вращающие моменты; увеличение индуктивных сопротивлений обмоток, вихревые токи в массивных проводниках и т.д.
Поэтому для их подавления применяют меры в основном за счет обмоточного коэффициента.
Используя известную тригонометрическую формулу каждый член суммы Σ можно представить в виде:
Fфνsin∙cosνα= 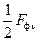 sin(ωt+να)+ sin(ωt+να)+ 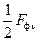 sin(ωt-να) sin(ωt-να)
| (4.4.15) |
Каждый из двух членов равенства представляет собой бегущую волну н.с., которая распределена в зазоре по гармоническому закону с амплитудой 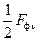 . Волны бегут навстречу друг другу. Докажем это.
. Волны бегут навстречу друг другу. Докажем это.
Допустим, мы наблюдаем за какими-либо точками этих двух волн, имеющими постоянные значения н.с. То есть
sin(ωt-να)=const,
sin(ωt+να)=const,
а следовательно:
ωt-να=const,
ωt+να=const.
Для того, чтобы показать, как должна изменяться во времени координата α, чтобы поддерживать выполнение последних равенств, продифференцируем их по времени:
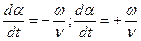 , ,
| (4.4.16) |
то есть одна волна – прямая, она вращается со скоростью 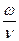 в сторону положительных значений α, другая – обратная (
в сторону положительных значений α, другая – обратная ( 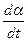 <0).
<0).
Сказанное можно проиллюстрировать рисунком (4.4.7).
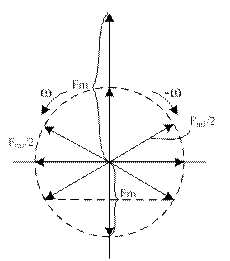
Рисунок 4.4.7 –Разложение пульсирующего поля на два вращающихся
Намагничивающая сила 3-фазной обмотки.
Пусть по 3-фазной обмотке текут симметричные токи:
ia= 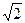 Isinωt;
ib= Isinωt;
ib= 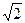 Isin(ωt- Isin(ωt- 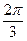 );
ic= );
ic= 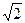 Isin(ωt- Isin(ωt- 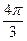 ) )
| (4.4.17) |
тогда в формуле для н.с. фаз В и С вместо ωt надо ставить ωt± 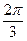 , а вместо να – ν(α±1200эл). Получим:
, а вместо να – ν(α±1200эл). Получим:
Faν= 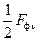 sin(ωt-να)+ sin(ωt-να)+ 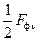 sin(ωt+να) sin(ωt+να)
| (4.4.18) |
Fbν= 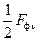 sin[ωt- sin[ωt- 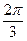 –ν(α- –ν(α- 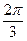 )]+ )]+ 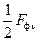 sin[ωt– sin[ωt– 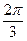 +ν(α- +ν(α- 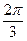 )] )]
| (4.4.19) |
Fcν= 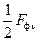 sin[ωt- sin[ωt- 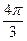 -ν(α- -ν(α- 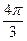 )]+ )]+ 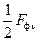 sin[ωt- sin[ωt- 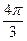 +ν(α- +ν(α- 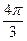 )] )]
| (4.4.20) |
Для получения суммарной н.с. 1-гармоники 3-фазной обмотки примем ν=1 и сложим 3 уравнения:
Fa1+Fb1+Fc1= 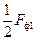 [sin(ωt-α)+sin(ωt+α)+sin(ωt-α)+sin(ωt+α- [sin(ωt-α)+sin(ωt+α)+sin(ωt-α)+sin(ωt+α- 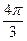 )+ +sin(ωt-α)+ sin(ωt+α- )+ +sin(ωt-α)+ sin(ωt+α- 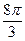 )]= )]= 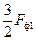 sin(ωt-α)
sin(ωt+α)+ sin(ωt+α- sin(ωt-α)
sin(ωt+α)+ sin(ωt+α- 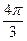 )+ sin(ωt+α- )+ sin(ωt+α- 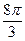 )= )=
| (4.4.21) |
Таким образом, н.с. 3-фазной обмотки равна:
F1== 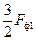 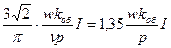 . .
| (4.4.22) |
В общем случае для m-фазной обмотки
F1= 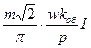
| (4.4.23) |
Можно показать, что н.с. 3-фазной обмотки не содержит гармоник, кратных трем и состоит из прямых (правобегущих) гармоник порядка ν=6k+1=1, 7, 13, 19, … и обратных ν=6k-1=5, 11, 17, …
Первая гармоника является прямой и вращается в направлении чередования фаз обмотки.
4.4.2 Магнитные поля и индуктивные сопротивления обмоток переменного тока.
Так же как и в трансформаторах, магнитный поток (поле), создаваемый каждой обмоткой делится на 1) основной поток; 2) поток рассеяния.
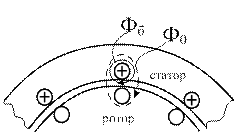
Рисунок 4.4.8 –Магнитное поле обмоток машин переменного тока
Основной поток (зазора) – это часть поля обмотки (статора), которая сцепляется с другой обмоткой (ротора) и создает в ней ЭДС основной частоты. Индуктивные сопротивления, соответствующие основному полю зазора называют главным индуктивным сопротивлением само- и взаимоиндукции.
Как известно, ЭДС переменного тока, которая индуктируется магнитным полем, созданным переменным током может быть выражена через соответствующее индуктивное сопротивление: Е=Ix, отсюда х = Е/I.
Э.д.с. самоиндукции, индуктируемая в обмотке статора потоком Ф1 основной гармоники определяется как
| E1=4,44f1WФ1, | (4.4.24) |
где W=Wфkоб – эффективное число проводников фазы.
| Ф1=Вср1τ1l=2Bmτ1l/π; | (4.4.25) |
Амплитуда индукции определяется через н.с. и магнитную проводимость:
| Bm=λδF1, | (4.4.26) |
где λδ=µ0/δ. Здесь полагалось, что δ=const.
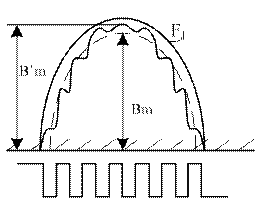
Рисунок 4.4.9 –Магнитное поле с учетом зубчатого строения ротора (статора)
Однако если учитывать зубчатое строение ротора, то, как видно из рисунка, необходимо ввести в анализ коэффициент воздушного зазора kδ, показывающий во сколько раз уменьшается амплитуда основной гармоники индукции под влиянием зубчатости:
kδ= 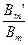 >1 >1
| (4.4.27) |
В этом случае проводимость уменьшается в kδ раз
λδ= 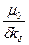 , ,
| (4.4.28) |
кроме того, следует учесть уменьшение В1 при наличии насыщения (мы полагаем, что µст=∞) с помощью kµ= 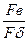 - коэффициента насыщения, тогда kµ=1,1÷1,5
- коэффициента насыщения, тогда kµ=1,1÷1,5
λδ= 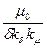 = = 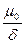 , ,
| (4.4.29) |
где 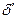 =δkδkµ - эквивалентный воздушный зазор.
=δkδkµ - эквивалентный воздушный зазор.
Н.с., создаваемая током статора:
F1= 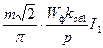 . .
| (4.4.30) |
Учитывая вышесказанное, получим:
Е1= 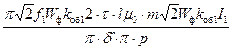 = = 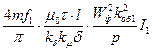 . .
| (4.4.31) |
Главное индуктивное сопротивление обмотки статора равно:
хг1= 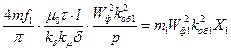 , ,
| (4.4.32) |
где –
Х1= 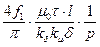 . .
| (4.4.33) |
Аналогично для ротора (АМ заторможенного, где f2=f1)
хг2= 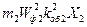 , ,
| (4.4.34) |
индуктивные сопротивления взаимной индукции:
- статора от основного поля ротора
хг21= 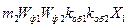
| (4.4.35) |
- ротора от основного поля статора:
хг12= 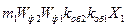
| (4.4.36) |
Из последних выражений видно, что хг21 ≠хг12, поскольку в общем случае m1≠m2.
Индуктивные сопротивления и поле рассеяния.
Поле рассеяния машины делится на следующие виды: пазовое, рассеяние по коронкам зубцов, лобовое, дифференциальное, рассеяние скоса.
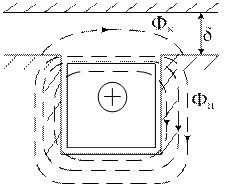
Рисунок 4.4.10 –Потоки пазового рассеяния и рассеяния по коронкам зубцов
Каждому из потоков рассеяния соответствует свое индуктивное сопротивление.
Поле пазового рассеяния пересекает паз прямолинейно, перпендикулярно его боковым стенкам. Его индуктивное сопротивление определяется как:
| xn=ωLn=Ψn/ik | (4.4.37) |
Величина Ψn определяется по сложным формулам и в конечном итоге зависит от:
| Ψn~ ik·λn·A, | (4.4.38) |
где λn – относительная магнитная проводимость рассеяния паза.
Поэтому xn~ λn·A, А – конструктивная характеристика машины, зависит от:f, Wk, q, p, µ0.
Поток рассеяния по коронкам зубцов создается силовыми линиями поля, которые замыкаются вокруг паза от одного зубца к другому, но не доходят до противоположной стороны зазора.
Соответствующее индуктивное сопротивление хк зависит от λк, которая определяется шириной паза и величиной зазора δ.
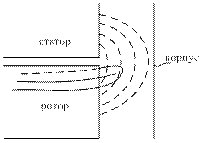
Рисунок 4.4.11 –Поле лобового рассеяния
Поле лобового рассеяния создается лобовыми частями обмоток и имеет сложную пространственную структуру. Поле лобовых частей статора сцепляются с лобовыми частями ротора и наоборот. Поэтому полями лобового рассеяния в обмотках наводятся э.д.с как само – так и взаимоиндукции. Однако последние значительно меньше первых и ими пренебрегают.
хл~λл~lл, kу, где lл – средняя длина лобовой части полувитка.
Как правило для расчета хn, хл и хк пользуются эмпирическими формулами.
Дифференциальное рассеяние.
Поскольку полезное действие машины основано на работе поля основной гармоники, то все остальные гармоники поля индуктируют в обмотках э.д.с. самоиндукции, определяемую индуктивным сопротивлением дифференциального рассеяния хд, которое определяется также, как Σхг, но с учетом, что ν=3,5,…
хд отличается от хг величиной коэффициента kд – дифференциального рассеяния хд=kдхг, который можно вычислить по формуле:
kд= 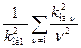 , ,
| (4.4.39) |
kд=0,002÷0,03.
Рассеяние скоса.
При скосе пазов или полюсов статора и ротора относительно друг друга рассеяние увеличивается т.к. э.д.с. и индуктивное сопротивление самоиндукции от основной гармоники поля не изменяется, а взаимоиндукции уменьшается. В этом случае рассеяние возникает за счет основной гармоники поля.
Итак, полное индуктивное сопротивление машины определяется суммой всех сопротивлений рассеяния:
хδ=хn+хк+хл+хд+хс.
Соотношение хг и хδ.
В машинах переменного тока хг>>хδ, как и в трансформаторах, но для МПТ хг меньше чем х12 в трансформаторах хг*=1,5÷10 (т.к. есть воздушный зазор), хδ*=0,08÷0,35.
АМ – главные составляющие: хг, хл и хд – поровну; (если есть, то хс, хк – мало)
СМ – хд<хn и хл, т.к. больше δ.
В ТГ хд мало, т.к. велико q.
Дата добавления: 2016-06-18; просмотров: 1879;











