МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
МОДЕЛЬ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
1 Математическое описание модели линейного программирования
2 Методы реализации моделей линейного программирования
3 Двойственная задача линейного программирования
Модель линейного программирования (ЛП) имеет место, если в исследуемой системе (объекте) ограничения на переменные и целевая функция линейны.
Модели ЛП используются для решения двух основных типов прикладных задач:
1) оптимального планирования в любых сферах человеческой деятельности – социальной, экономической, научно-технической и военной. Например, при оптимальном планировании производства: распределении финансовых, трудовых и других ресурсов, снабжении сырьем, управлении запасами и т. д.
2) транспортной задачи (нахождение оптимального плана различного рода перевозок, оптимального плана распределения разных средств по объектам различного назначения и т. п.)
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Требуется найти неотрицательные значения переменных
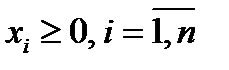 ,
,
удовлетворяющих  линейным ограничениям в виде равенств и неравенств
линейным ограничениям в виде равенств и неравенств
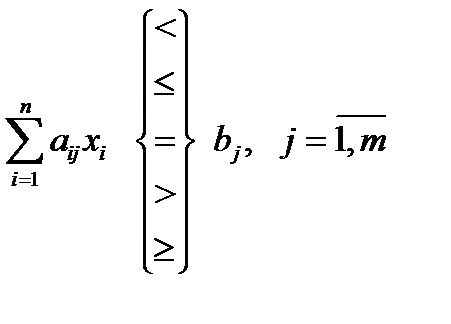 ,
,
где 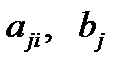 – заданные числа,
– заданные числа,
и обеспечивающих экстремум линейной целевой функции
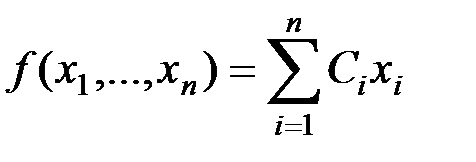 ,
,
где 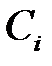 – заданные числа, что записывается в виде
– заданные числа, что записывается в виде
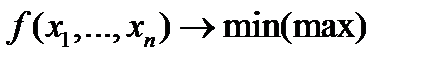 .
.
Допустимым решением называется любая совокупность 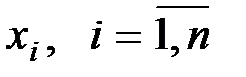 , удовлетворяющих условиям.
, удовлетворяющих условиям.
Область допустимых решений 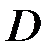 – множество всех допустимых решений.
– множество всех допустимых решений.
Оптимальное решение 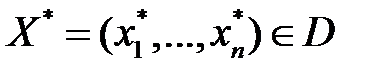 , для которого
, для которого 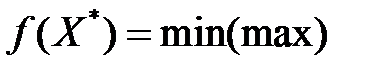 .
.
Замечания
1. Приведенная модель ЛП является общей. Различают также стандартные и канонические формы моделей ЛП.
2. Условия существования реализации модели ЛП:
– множество допустимых решений 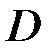 – не пустое;
– не пустое;
– целевая функция 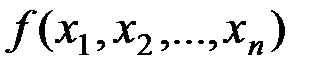 ограничена на
ограничена на 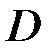 (хотя бы сверху при поиске максимума и снизу при поиске минимума).
(хотя бы сверху при поиске максимума и снизу при поиске минимума).
3.ЛП основывается на двух теоремах
Теорема 1. Множество G, определяемое системой ограничений вида, есть выпуклое замкнутое множество (выпуклый многогранник в 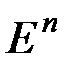 с угловыми точками - вершинами.)
с угловыми точками - вершинами.)
Теорема 2. Линейная форма 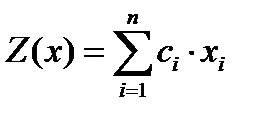 , определенная на выпуклом многограннике
, определенная на выпуклом многограннике
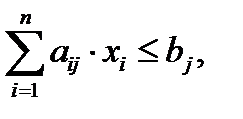 j=1,2,…,s
j=1,2,…,s
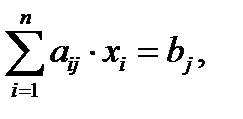 i=s+1,s+2,…,m,
i=s+1,s+2,…,m,
достигает экстремума в одной из вершин этого многогранника.
Данная теорема получила название теоремы об экстремуме линейной формы.
В соответствии с теоремой Вейерштрасса оптимальное решение единственно и является глобальным экстремумом.
Существует общий аналитический подход к реализации модели ЛП – симплекс-метод. При решении задач линейного программирования достаточно часто решения нет. Это происходит по следующим причинам.
Первую причину проиллюстрируем примером
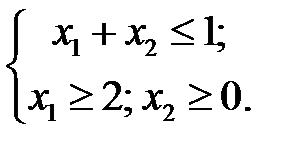
Про такую причину говорят, что ограничения несовместны. Область допустимых решений – пустое множество.
Вторая причина комментируется следующим примером:
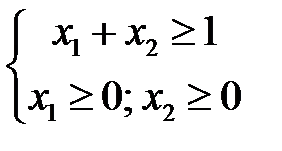
В данном случае, область допустимых решений не ограничена сверху. Область допустимых решений не ограничена.
Следуя традициям линейного программирования, дадим задаче ЛП экономическую интерпретацию. Пусть в нашем распоряжении имеется m типов ресурсов. Количество ресурса типа j равно 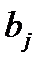 . Эти ресурсы необходимы для производства n типов товаров. Обозначим количество этих товаров символами
. Эти ресурсы необходимы для производства n типов товаров. Обозначим количество этих товаров символами 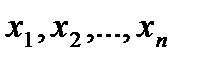 соответственно. Единица товара типа i стоит
соответственно. Единица товара типа i стоит 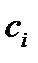 . Производство товаров типа i должно быть ограничено величинами
. Производство товаров типа i должно быть ограничено величинами 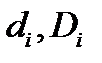 соответственно. На производство единицы товара типа i расходуется
соответственно. На производство единицы товара типа i расходуется 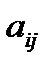 ресурса типа j. Необходимо определить такой план производства товаров (
ресурса типа j. Необходимо определить такой план производства товаров ( 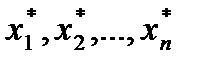 ), чтобы их суммарная стоимость была минимальной.
), чтобы их суммарная стоимость была минимальной.
Задачи линейного программирования, используемые для оптимизации функционирования реальных объектов, содержат значительное число переменных и ограничений. Это обуславливает невозможность решения их графическими методами. При большом числе переменных и ограничений применяются алгебраические методы, в основе которых лежат итерационные вычислительные процедуры. В линейном программировании разработано множество алгебраических методов, различающихся между собой способами построения начального допустимого решения и условиями перехода от одной итерации к другой. Однако все эти методы базируются на общих теоретических положениях.
Общность основных теоретических положений приводит к тому, что алгебраические методы решения задач линейного программирования во многом сходны между собой. В частности, практически любой из них требует предварительного приведения задачи линейного программирования к стандартной (канонической) форме.
Алгебраические методы решения задачи ЛП начинаются с приведения ее к стандартной (канонической) форме:
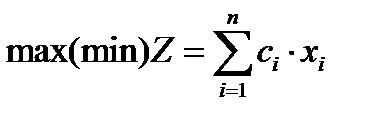 ,
,
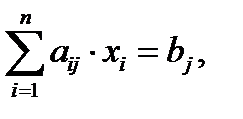
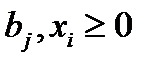 ,
,
i=1,..,n; j=1,..,m.
Любая задача линейного программирования может быть приведена к стандартной форме. Сравнение общей модели с канонической моделью позволяет сделать вывод о том, что для приведения задачи ЛП к стандартной форме необходимо, во-первых, от системы неравенств перейти к равенствам, а во-вторых, преобразовать все переменные так, чтобы они были неотрицательными.
Переход к равенствам осуществляется прибавлением к левой части ограничений неотрицательной остаточной переменной для неравенств типа 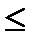 , и вычитанием из левой части неотрицательной избыточной переменной для неравенств типа
, и вычитанием из левой части неотрицательной избыточной переменной для неравенств типа 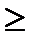 . Например, неравенство
. Например, неравенство 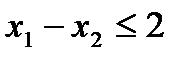 при переходе к стандартной форме преобразуется в равенство
при переходе к стандартной форме преобразуется в равенство 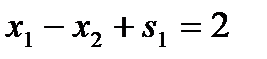 , a неравенство
, a неравенство 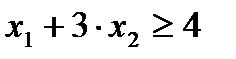 - в равенство
- в равенство 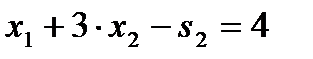 . При этом, как остаточная переменная
. При этом, как остаточная переменная 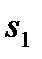 , так и избыточная переменная
, так и избыточная переменная 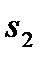 являются неотрицательными.
являются неотрицательными.
Предполагается, что правая часть неравенств неотрицательна. В противном случае, этого можно добиться умножением обеих частей неравенства на «-1» и сменой его знака на противоположный.
Если в исходной задаче линейного программирования переменная 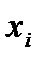 не ограничена в знаке, ее можно представить в виде разности двух неотрицательных переменных
не ограничена в знаке, ее можно представить в виде разности двух неотрицательных переменных 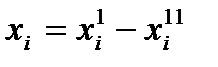 , где
, где 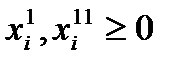 .
.
Важной особенностью переменных 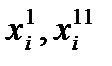 является то, что при любом допустимом решении только одна из них может принимать положительное значение. Это означает, что если
является то, что при любом допустимом решении только одна из них может принимать положительное значение. Это означает, что если 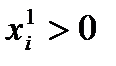 , то
, то 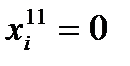 и наоборот. Следовательно,
и наоборот. Следовательно, 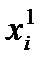 может рассматриваться как остаточная, а
может рассматриваться как остаточная, а 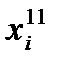 - как избыточная переменные.
- как избыточная переменные.
ПримерПусть дана задача линейного программирования:
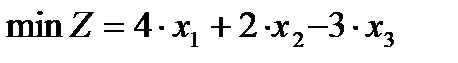 ,
,
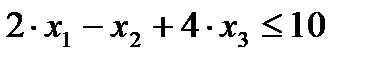 ,
,
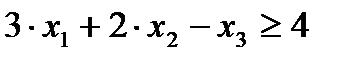 ,
,
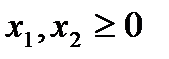 .
.
Необходимо привести ее к стандартной форме. Заметим, что первое неравенство исходной задачи имеет знак 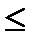 , следовательно, в него необходимо ввести остаточную переменную
, следовательно, в него необходимо ввести остаточную переменную 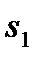 . В результате получим
. В результате получим 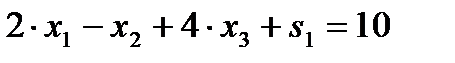 .
.
Второе неравенство имеет знак 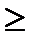 и для преобразования к стандартной форме требует введения избыточной переменной
и для преобразования к стандартной форме требует введения избыточной переменной 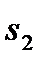 , выполнив эту операцию, получим
, выполнив эту операцию, получим 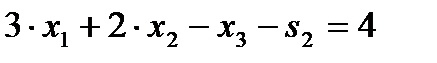 .
.
Кроме того, переменная 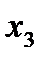 не ограничена в знаке. Следовательно, как в целевой функции, так и в обоих ограничениях она должна быть заменена на разность
не ограничена в знаке. Следовательно, как в целевой функции, так и в обоих ограничениях она должна быть заменена на разность 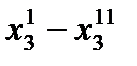 . Выполнив подстановку, получим задачу линейного программирования в стандартной форме, эквивалентную исходной задаче:
. Выполнив подстановку, получим задачу линейного программирования в стандартной форме, эквивалентную исходной задаче:
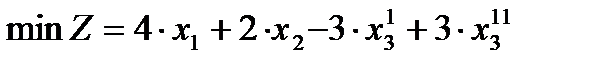 ,
,
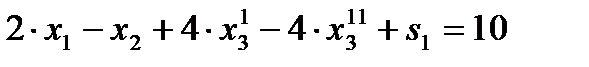 ,
,
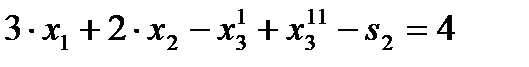 ,
,
 .
.
Задача линейного программирования, записанная в стандартной форме, представляет собой задачу поиска экстремума целевой функции на множестве векторов, являющихся решениями системы линейных уравнений с учетом условий неотрицательности. Как известно, система линейных уравнений может не иметь решений, иметь единственное решение или иметь бесконечное множество решений. Оптимизация целевой функции возможна только в том случае, если система имеет бесконечное множество решений. Система линейных уравнений имеет бесконечное множество решений, если она совместна (ранг основной матрицы равен рангу расширенной) и, если ранг основной матрицы меньше числа неизвестных.
Пусть ранг матрицы системы ограничений равен m. Это значит, что матрица имеет хоть один минор m-го порядка не равный нулю. Не нарушая общности, можно предположить, что минор расположен в левом верхнем углу матрицы. Этого всегда можно добиться, изменив нумерацию переменных. Этот не равный нулю минор ранга m принято называть базисным. Составим систему из первых m уравнений системы, записав ее следующим образом:
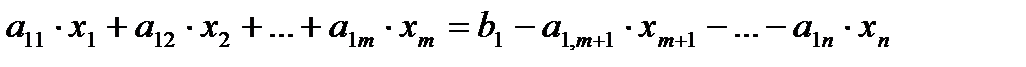 ,
,
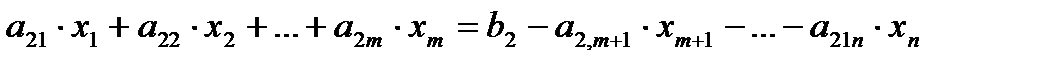 ,
,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
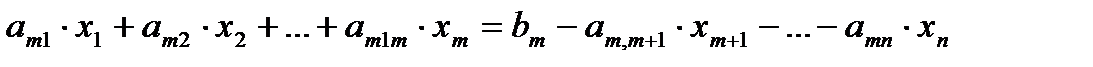
Если неизвестным 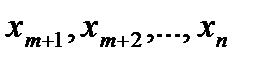 назначить произвольные фиксированные значения, то в правой части каждого линейного уравнения получаются числа, и исходная система превращается в систему из m уравнений с m неизвестными. Причем определитель этой системы есть не равный нулю базисный минор.
назначить произвольные фиксированные значения, то в правой части каждого линейного уравнения получаются числа, и исходная система превращается в систему из m уравнений с m неизвестными. Причем определитель этой системы есть не равный нулю базисный минор.
Следовательно, при фиксированных 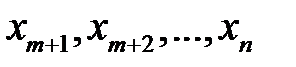 система имеет единственное решение. Решение, соответствующее нулевым значениям переменных
система имеет единственное решение. Решение, соответствующее нулевым значениям переменных 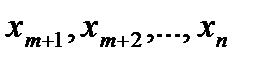 , называется базисным решением. Для системы линейных уравнений с n неизвестными, имеющей ранг основной матрицы равный m, количество базисных миноров а, следовательно, и количество базисных решений определяется из соотношения
, называется базисным решением. Для системы линейных уравнений с n неизвестными, имеющей ранг основной матрицы равный m, количество базисных миноров а, следовательно, и количество базисных решений определяется из соотношения
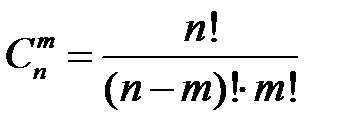 .
.
Базисное решение, удовлетворяющее условию неотрицательности переменных, называется допустимым базисным решением. Понятие допустимого базисного решения является исключительно важным в линейном программировании. Как будет ясно из дальнейшего, все допустимые решения задачи линейного программирования могут быть выражены через множество ее допустимых базисных решений. Более того, целевая функция достигает экстремума на одном из допустимых базисных решений.
Задачу линейного программирования можно решить, отыскав все ее допустимые базисные решения и выбрав среди них то, которому соответствует максимум целевой функции. Но, как следует из формулы, число таких решений может оказаться очень большим. Поэтому на практике предпочитают использовать направленный перебор допустимых базисных решений. При направленном переборе каждое следующее базисное решение оказывается ближе к оптимуму, чем предыдущее, что значительно сокращает общее число вычислений.
Проиллюстрируем наличие базиса и базисного решения на примере задачи о предприятии. Приведем еще раз формальную постановку задачи:
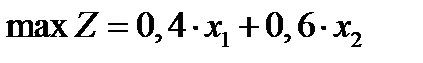 ,
,
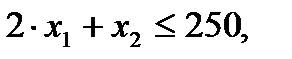
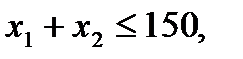
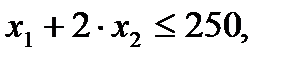
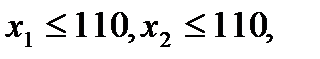
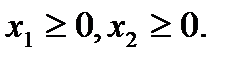
Преобразуем задачу к стандартному виду. Для этого введем во все пять неравенств добавочные переменные 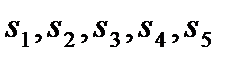 .В результате получим
.В результате получим
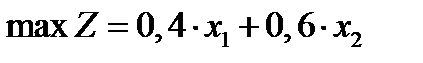 ,
,
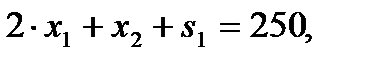
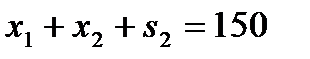 ,
,
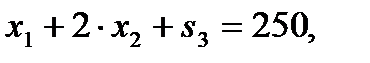
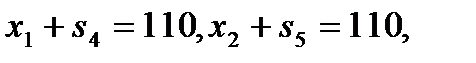
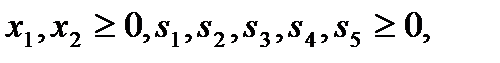
Система линейных уравнений имеет 7 неизвестных: 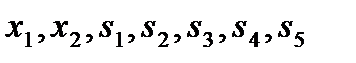 . Поскольку минор, составленный из остаточных переменных
. Поскольку минор, составленный из остаточных переменных 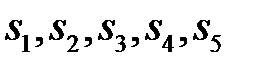 , не равен нулю, ранг основной матрицы этой системы равен 5. Легко видеть, что ранг расширенной матрицы также равен пяти. Следовательно, система уравнений имеет бесконечное множество решений. Количество базисных решений равно
, не равен нулю, ранг основной матрицы этой системы равен 5. Легко видеть, что ранг расширенной матрицы также равен пяти. Следовательно, система уравнений имеет бесконечное множество решений. Количество базисных решений равно 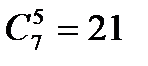 . Каждое базисное решение содержит два нулевых и пять ненулевых компонент.
. Каждое базисное решение содержит два нулевых и пять ненулевых компонент.
Дата добавления: 2016-05-28; просмотров: 4182;










