Статистическое тестирование ПСП и генераторов
С учетом изложенного, будем считать последовательность символов некоторого алфавита псевдослучайной в узком смысле, если никакой алгоритм из некоторого набора полиномиальных алгоритмов не может ее отличить от случайной.
Алгоритмы этого набора будем называть тестами (критериями) на случайность, а процесс проверки последовательности – тестированием. Если тест не смог отличить последовательность от случайной, то будем говорить, что последовательность проходит или выдерживает, данный тест. В противном случае, будем говорить, что тест отклоняет последовательность.
Итак, вопрос о проверке случайности последовательности сводится к вопросу построения соответствующего набора тестов. Для этого вначале необходимо определить принцип их работы, а именно: каким образом тест должен принимать одни последовательности и отклонять другие?
Одним из ответов на этот вопрос является проверка наличия у заданной последовательности некоторого свойства, характерного для любых случайных последовательностей.
Например, пусть элементы последовательности выбираются независимо и равновероятно из множества Z2. В этом случае последовательность из n единиц, плохо подходит на роль случайной для практических применений, хотя вероятность ее появления равна 2-n, как и любой другой реализации из множества 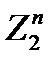 .
.
Однако она не будет типовой с точки зрения появления в РРСП (достаточно большой длины) существенного дисбаланса между числом единиц и нулей. В тоже время, предпочтительно считать типовой последовательность, у которой количество единиц и нулей отличаются несущественно.
В дальнейшем тесты, построенные на свойствах встречаемости элементов последовательности, будем называть частотными, так как они проверяют распределение частот встречаемости и выявляют его отклонение от равновероятного распределения (в т.ч.: критерии χ2, максимального правдоподобия и максимальной частоты).
Возвращаясь к работе теста, заметим, что его результатом всегда будет принятие или отклонение гипотезы Н0, которая предполагает, что конкретная последовательность является последовательностью независимых, равномерно распределенных случайных величин. Ее альтернативой будем считать сложную гипотезу Н1, которая включает все возможные неравномерные распределения элементов последовательности, так и все возможные виды зависимостей между ними.
Получив результаты тестирования некоторой последовательности, мы делаем вывод о ее происхождении с достаточно большой (но меньше 1) вероятностью, которая зависит от параметров теста. С каждым тестом связаны два параметра:
α – вероятность ошибки1-го рода - вероятность отклонить истинно случайную последовательность, т.е. принять гипотезу Н1, в то время как верна гипотеза Н0. Величина α также называется уровнем значимости теста;
β – вероятность ошибки2-го рода - вероятность принять неслучайную последовательность за случайную, т.е. принять гипотезу Н0 при условии, что верна гипотеза Н1.
Уровень значимости задается до начала работы теста, при этом он определяет относительную часть чисто случайных последовательностей, которые не обладают свойствами, наличие которых проверяет тест. Обычно α выбирается из практических соображений. Если вероятность поверяемой гипотеза достаточно высока, то уровень значимости выбирается маленьким (10-2-10-3).
Параметр β зависит от α и длины последовательности n так, при фиксированном α с ростом n величина β уменьшается. Поскольку гипотеза Н1 сложная, то из множества тестов нельзя выбрать единый тест, который соответствует равномерно наиболее мощному критерию, т.е. такой, который при заданном уровне значимости α минимизирует значение β.
В ходе работы теста, исходя из тестируемой последовательности, вычисляется некоторая величина U, называемая статистикой. Будем говорить, что тест принимает последовательность, если U≤Uα, где Uα – называется пороговым значением статистики. Тест называется двусторонним, если при его проверке используется неравенство |U|≤Uα.
Величина Uα находится из соотношения F(Ua)=1-a, где F ‑ функция распределения вероятностей, α – уровень значимости теста. Поскольку функция F – возрастающая, то вместо сравнения U и Uα можно сравнивать F(U) и F(Ua). Значение PU=1-F(U) называется P-величиной.
Итак, последовательность считается случайной, если PU≥α.
Величины α и PU являются вероятностями того, что случайная последовательность будет иметь значение статистики больше чем Uα и U соответственно.
Например, для проверки вида распределения тестируемой последовательности можно воспользоваться статистикой c2:
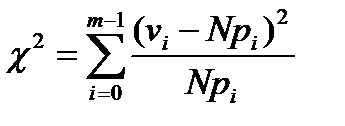
| (1) |
Где vi – частота встречаемости символа iÎZm в последовательности знаков шифрованного текста, N=n0+…+nm-1 – длина тестируемой последовательности, (p0,…,pm-1) – вектор вероятностей, соответствующий гипотезе Н0. Доказано, что статистика (1) при N®¥ имеет распределение Пирсона с m-1 степенями свободы.
В случае РРСП имеем (p0,…,pm-1)=(1/m,…,1/m), пусть величина 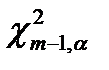 ‑ квантиль распределения c2 с m-1 степенью свободы, соответствующий уровню значимости a, т.е.:
‑ квантиль распределения c2 с m-1 степенью свободы, соответствующий уровню значимости a, т.е.:
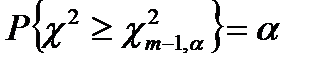
|
Если для выборки выполняется неравенство:
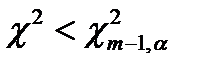
| (2) |
то принимается гипотеза Н0 о случайном характере последовательности, в противном случае – гипотеза Н0 отвергается.
Отметим, что согласие экспериментальных данных с гипотезой о наличии у последовательности определенного свойства не свидетельствует о противоречии этих же данных с другой гипотезой. На основе наблюдения реализации последовательности с помощь статистических критериев нельзя доказать справедливость той или иной гипотезы, а можно лишь утверждать, что результаты наблюдений не противоречат данной гипотезе.
Рассмотрим основные требования к набору тестов. Ясно, что набор должен содержать некоторое минимально необходимое множество тестов, которое определяется будущим применением тестируемых последовательностей и может быть различным в каждом конкретном случае.
Например, набор тестов, рекомендованный Национальным институтом стандартов США ‑ NIST для тестирования двоичных последовательностей [5], включает 16 тестов (в т.ч. тесты: частотный монобитный; частотный блочный; тесты серий и длинных серий единиц; ранга случайной {0,1}-матрицы и др.).
Большинство тестов из набора NIST предназначены для тестирования двоичных последовательностей длиной от 103 –106, однако некоторые из них могут использоваться для тестирования последовательностей длиной от 102 элементов (монобитный и блочный частотные тесты, тест серий, тест серий максимальной длины, тест частот v-грамм с перекрытием и др.). Можно создать аналоги тестов этого набора для тестирования последовательностей элементов из произвольного алфавита.
Количество тестов в некотором их наборе определяется исходя из так называемой общей ошибки 1-го рода, т.е. той части случайных последовательностей, которые не пройдут хотя бы один из тестов.
Общая ошибка 1-го рода A(n,a) находится для заданных ошибок 1-го рода каждого из тестов при условии их независимости. Если для всех тестов задана одно значение a, то вероятность того, что случайная последовательность не пройдет, по крайней мере, один тест из набора равна:
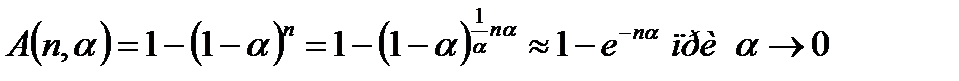
|
Для заданной величины А количество тестов определяется из уравнения:
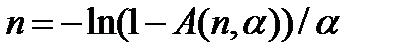
|
Заметим, что с ростом n величина А стремится к 1:
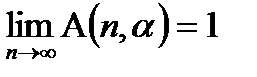
|
а потому количество тестов не должно быть чрезмерно большим.
Пример. Если в каждом из 16 тестов из набора, рекомендованного NIST, ошибка 1-го рода равна 0.01, то A(n,a)=0.15, т.е.около 15% чисто случайных последовательностей не пройдет хотя бы один из тестов набора.
Как уже было отмечено, тестированию подлежат:
· криптографические свойства конкретных последовательностей;
· свойства генератора, используемого для создания случайных последовательностей.
Для статистики наиболее существенной особенностью любой последовательности является ее длина. На практике отдельно рассматриваются вопросы тестирования последовательностей “большой” и “малой” длины. Основной причиной дифференцированного подхода к этим двум случаям является тот факт, что свойства случайной последовательности становятся тем более выразительными, чем больше ее длина.
Считается, что минимальная длина последовательности для частотных тестов должна быть в 5-10 раз больше объема алфавиту. В таком случае при условии равномерного распределения символов последовательности вероятность того, что каждый символ встретится, по меньшей мере, 1 раз близка к единице.
Действительно, в этих условиях вероятность того, что какой-то символ не встретился ни разу, чрезвычайно мала:
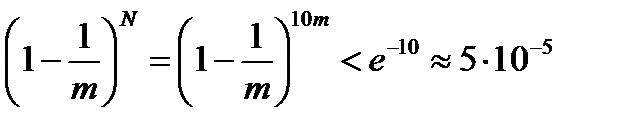
|
Другие тесты могут предъявлять еще более жесткие требования к длине последовательности.
Поскольку, любая подпоследовательность РРСП также является РРСП, наряду с тестированием всей реализации необходимо тестировать ее разные подпоследовательности. Эти подпоследовательности должны выбираться с помощью некоторых правил, причем так, чтобы символ, который выбирается, не зависел бы от своего значения. В частности, нельзя выбирать подпоследовательность, которая состоит только из нулей.
Правила выбора подпоследовательностей могут быть следующими:
· каждый j-ый элемент исходной последовательности;
· каждый элемент, перед которым встречается некоторая фиксированная комбинация символов;
· элементы, номера мест которых определяются некоторой последовательностью, независимой от данной и т.д.
Тестирование генераторов случайных последовательностей (чисел) состоит из двух этапов:
· тестирование достаточного количества (»103) последовательностей с помощью подобранного набора тестов;
· обработка полученных результатов.
Для генератора случайных последовательностей должны выполняться следующие соображения:
· если последовательность испытывается тестом, для которого задан уровень значимости α, то с вероятностью α последовательность не пройдет этот тест. Например, при α=0.01 в среднем 1 из 100 последовательностей не пройдет тест;
· на выходные последовательности генератора должны иметь равномерное распределение соответствующих им значений PU.
Методика NIST обработки результатов тестирования генераторов предполагает следующие действия:
1. Вычисление пропорции последовательностей, которые прошли тест: Пусть было протестировано k последовательностей, из них k* прошли тест. Тогда пропорция равняется k*/k. Если уровень значимости теста равен α, то должно выполняться неравенство:
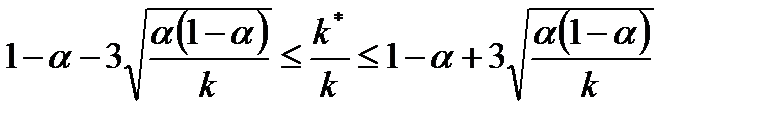
| (1) |
2. Проверка равномерности распределения P-величин:
Подсчитываются числа: Fi – количество P-величин, принадлежащих интервалу [0.1×(i-1),0.1×i), где i=1,…,10, после чего вычисляется статистика:
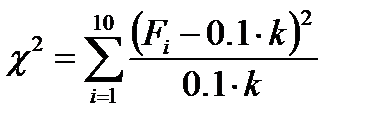
|
Находится значение PT=igams(4.5,0.5×c2), где igams – неполная гамма-функция; вычисляемая по формуле:
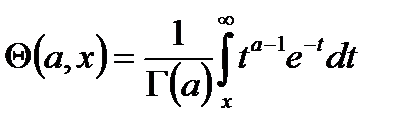 , где , где 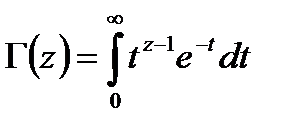
|
Если выполняется неравенство
| PT≥0.0001, | (2) |
то P-величины считаются равномерно распределенными.
Генераторы, для которых выполняется (1), (2), по терминологии NIST [5] называются одобренными (approved).
Генератор со свойствами (1) и (2) в зависимости от набора тестов может быть достаточно хорош для формирования гаммы однократного использования и других криптографических приложений.
Заключна частина
Формування якісної с криптографічної точки зору послідовності фактично еквівалентно задачі побудови надійного криптографічного алгоритму, оскільки в обох випадках виникає поняття однобічної функції, яку легко розрахувати, але досить складно обернути.
Оскільки безпека криптографічного захисту інформації базується на секретності ключу, це потребує від дослідників, розробників, виробників та користувачів засобів та систем КЗІ постійного вдосконалення рівня спеціальної підготовки та врахування останніх наукових досліджень повсякденній діяльності.
Дата добавления: 2016-06-15; просмотров: 2904;











