Расчет равновесного состава газовой смеси
При протекании гомогенной обратимой реакции в газовой фазе после установления химического равновесия в системе будут присутствовать как продукты реакции, так и исходные вещества. Зная уравнение химической реакции, величину константы равновесия и начальные концентрации реагентов, можно рассчитать равновесные концентрации всех веществ. Их величины будут зависеть от температуры и давления.
Необходимо отметить, что в достаточно широкой области давлений и температур газовые смеси можно считать идеальными и проводить расчеты равновесного состава газовой смеси, считая коэффициент фугитивности gi @ 1.
Реакции в газовой фазе протекают в относительно широком интервале температур и давлений. Константы равновесия для каждой конкретной реакции, как правило, рассчитываются с использованием табличных значений термодинамических функций реагирующих веществ для определенных температури давлений.
Пусть протекает обратимая газовая реакция nAA + nBB ÛnDD + nEE. С использованием термодинамических характеристик реакции (DrG0(T),DrH0(T),DrS0(T)) рассчитывается стандартная константа равновесия К0(Т) для определенной температуры Т:
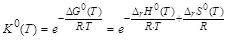 .
.
Из стандартной константы равновесия К0(Т) рассчитывают константы равновесия КX(Т, p) и Кр(Т). Отметим, что величина КX(Т, p) зависит от давления, а Кр(Т) не зависит:
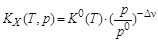 ,
, 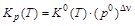 ,
,
где р0 = 1,013×105 Па – стандартное давление; Dn= (nD + nE)–(nA + nB) –изменение числа молей в ходе реакции.
Расчет равновесного состава продуктов реакции для изобарного процесса проводят с использованием мольных долей (Xi) и соответственно КX, а для изохорного процесса с использованием парциальных давлений реагентов (рi) и соответственно Кр.
Рассмотрим расчет равновесного состава продуктов реакции, протекающей при постоянном давлении.
Пусть в начальный момент времени в системе содержится соответственно nA, nB, nD, nE молей реагентов и к моменту наступления равновесия прореагирует x молей вещества А. Тогда в результате реакции число молей исходных веществ и продуктов изменится и станет равным соответственно nA- x, nB- 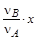 , nD+
, nD+ 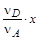 , nE+
, nE+ 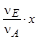 .
.
Мольная доля i-го вещества в равновесной смеси равна:
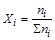 ,
,
где Sni – суммарное число молей всех веществ в системе в состоянии равновесия,
Sni =(nA- x)+( nB- 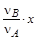 )+( nD+
)+( nD+ 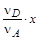 )+( nE+
)+( nE+ 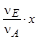 ).
).
Константа равновесия данной реакции
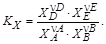
Подставив в константу равновесия соответствующие выражения для мольных долей реагентов, получим уравнение с одним неизвестным x. Его решение позволяет рассчитать равновесный состав газовой смеси.
Примеры.
1. Рассчитать состав равновесной газовой смеси, получающейся в результате взаимодействия эквивалентной смеси водорода и азота по реакции 3H2 + N2 Û 2NH3 при давлении р и температуре Т = 700 К. Рассчитать выход аммиака.
Решение.
А. Расчет константы равновесия KX (Т, р).
Определяем изменение энергии Гиббса при протекании реакции
3H2 + N2 Û 2NH3
DfH0298, кДж/моль 0 0 –45,94
S0298, Дж/моль×K 130,52 191,50 192,66
Изменение энергии Гиббса при температуре Т = 700 К DrG0(700) можно вычислить по энтальпии и энтропии реакции при Т=298 К,
DrG0(Т) »DrН0298– Т×DrS0298,
DrН0298=(å ni×DfН0298i)продукты–(å ni×DfН0298i)исх. вещества,
DrS 0298=(åni×S0298i)продукты– (åni×S0298i) исх. вещества,
DrН0298 = 2× (–45,94) – (3×0 +1×0) = –91,88 кДж,
DrS 0298 = 2× (192,66) – (3×130,52 +1×191,50)= –197,74 Дж/K,
DrG0298 = –91,88 ×103– 700×(–197,74) = 46540Дж.
Рассчитываем величину 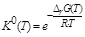 и
и 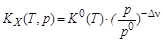 :
:
К0(700)=3,37×10-4, KX(700)= К0(700)×(p/p0)–Dn= К0(700)×( 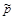 )–Dn,
)–Dn,
Dn =(2)–(3+1)= –2.
Б.) Расчет состава (мольные доли) газовой смеси в состоянии равновесия при 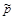 =1 атм (KX = К0).
=1 атм (KX = К0).
Поскольку водород и азот в начальный момент времени находятся в эквивалентных количествах, то на 3 моля водорода приходится 1 моль азота. Пусть к моменту прихода системы к равновесию израсходовалось x молей азота. Тогда в равновесной газовой смеси будет приходиться на nН2=3–3×x молей водорода в соответствии с уравнением реакции nN2=1–x молей азота и nNH3=2×x молей аммиака:
3H2 + N2 Û 2NH3
3-3×x 1-x +2×x
Суммарное число молей веществ в равновесной смеси
Sni = (3–3×x)+(1–x)+(2×x) =2× (2–x).
Тогда мольная доля i-го вещества будет равна соответственно:
XH2= 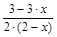 , XN2=
, XN2= 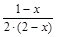 , XNH3=
, XNH3= 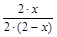 .
.
Константа равновесия KX будет равна:
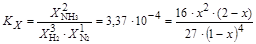 .
.
Условию задачи соответствует решение данного уравнения x= 0,0117.
Определив x,можно рассчитать мольные доли (Xi) компонентовв равновесной газовой смеси. Результаты расчета приведены в табл. 3.1.
Если бы реакция была необратима, то из 3 молей водорода и 1 моля азота образовалось бы 2 моля аммиака. Расчет показывает, что вследствие обратимости реакции в этих условиях образовалось только 2×x=0,00234 молей аммиака. Таким образом, выход целевого продукта составил величину (0,0234 /2)×100%=1,17%. Увеличить выход целевого продукта можно сместив равновесие, например изменив давление. Результаты расчета приведены в табл. 3.1.
Таблица 3.1
Состав (мольные доли компонентов Xi) равновесной газовой смеси реакции
3H2 + N2 Û 2NH3 при Т=700 К при различных давлениях
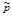 , атм , атм
| H2 | N2 | NH3 | Выход NH3, % |
| 0,746 | 0,294 | 0,006 | 1,17 | |
| 0,663 | 0,221 | 0,116 | 20,8 | |
| 0,605 | 0,202 | 0,194 | 32,5 | |
| 0,528 | 0,176 | 0,296 | 45,6 |
Данные таблицы показывают, что увеличение давления приводит к увеличению выхода аммиака.
2. Расчет степени термической диссоциации тетрооксида диазота (N2О4) по реакции N2О4 Û 2 NО2 при температуре Т и давлении р.
Решение.
А. Расчет константы равновесия KX (Т, р).
Определяем изменение энергии Гиббса при протекании реакции
N2О4 Û 2 NО2
DfH0298, кДж/моль 11,11 34,19
S0298, Дж/моль×K 304,35 240,06
Изменение энергии Гиббса при температуре Т DrG0(Т) можно вычислить по энтальпии и энтропии реакции при Т=298 К:
DrG0(Т)» DrН0298– Т×DrS0298,
DrН0298= (å ni×DfН0298i)продукты–(å ni×DfН0298i)исх. вещества ,
DrS 0298=(åni×S0298i)продукты–(åni×S0298i) исх. вещества ,
DrН0298 = 2× (34,19) – (11,11) = 57,27 кДж,
DrS 0298 = (2×240,06) – 304,35 = 175,77 Дж/K,
DrG0298 = 57,27×103–323×175,77 = 496,29 Дж.
Рассчитываем величину 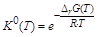 и
и 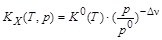 .
.
Поскольку для данной реакции Dn =(2)–(1)= +1, то
KX(T, р)= К0(T)×(p/p0)–1= К0(T)×( 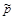 )–1
)–1
Б. Расчет состава (мольные доли) газовой смеси в состоянии равновесия.
Пусть к моменту равновесия из каждого моля N2О4 распалось x молей. Тогда в равновесной газовой смеси будет приходиться на nN2О4= 1–x молей тетрооксида диазота nNО2= 2×x молей диоксида азота:
N2О4 Û 2 NО2
1–x 2×x
Суммарное число молей N2О4 и NО2 в равновесной смеси:
Sni = (1–x) + (2×x) = 1+x.
Тогда мольная доля веществ в равновесной смеси Xi=ni/Sni будет равна:
XN2О4= 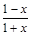 , XNО2=
, XNО2= 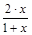 .
.
Для константы равновесия KX можно написать:
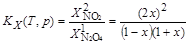
откуда x = 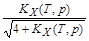 .
.
В. Расчет степени диссоциации N2О4.
Степень диссоциации (a) – это доля молекул вещества от их начального количества, которая подверглась диссоциации. Поскольку к моменту равновесия из одного моля N2О4 распалось на NО2 x молей, то x º a:
a(T, p)= 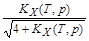 .
.
Таким образом, степень диссоциации N2О4 зависит от температуры и давления. Например, при Т=100°С и 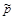 =1атм
=1атм
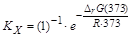 =14,50, a= 0,885, XN2O4= 0,061, XNO2= 0,939.
=14,50, a= 0,885, XN2O4= 0,061, XNO2= 0,939.
 Результаты аналогичных расчетов для реакции диссоциации N2О4 в графическом виде представлены на рис.3.2.
Результаты аналогичных расчетов для реакции диссоциации N2О4 в графическом виде представлены на рис.3.2.
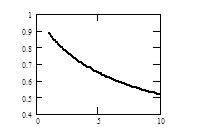

Рис. 3.2. Зависимость степени диссоциации N2О4 (a) от давления р при постоянной температуре Т=100°С (а) и от температуры Т при постоянном давлении р=1атм(б)
Степень диссоциации N2О4 является количественной характеристикой смещения равновесия реакции N2О4 Û 2 NО2. При a®1 равновесие в системе смещено в сторону образования продуктов диссоциации. Увеличение давления приводит к уменьшению a, а увеличение температуры – к увеличению a. Эти закономерности полностью соответствуют выводам анализа уравнений изобары и изотермы реакции.
Дата добавления: 2020-02-05; просмотров: 677;











