Основи масопередачі.

У хімічній технології велике значення мають процеси массопередачи, які полягають в переході речовини (маси) з однієї фази в іншу. Причиною, що викликає перерозподіл рідкого або газоподібного компоненту між фазами, є різний вміст цього компоненту у фазах.

Застосовуючи процес массопередачи, можна здійснювати розділення сумішей різних речовин на компоненти. Ці суміші можуть бути неоднорідними гетерогенними або однорідними гомогенними системами, розділення яких представляє найбільші труднощі.

Масообмінні процеси відбуваються при розділенні двокомпонентних і багатокомпонентних сумішей на окремі компоненти або рідше при змішенні компонентів.

Процеси теплопередачі і масопередачі багато в чому аналогічні, хоча між ними є і істотні відмінності. Рушійною силою процесів теплопередачі є різниця температур між тими, що обмінюються теплом середовищами, рушійною силою процесів масопередачі— різниця концентрацій між фазами. Проте якщо в процесах теплопередачі поверхня теплообміну, як правило, відома, то визначити при масообміні поверхню контакту між фазами у вигляді окремих струменів газу або пари з бульбашками, бризками, піною рідини або твердими частинками украй важко, оскільки величина цієї поверхні постійно міняється.

У хімічній промисловості застосовуються наступні процеси, засновані на явищах масопередачі.

Абсорбція — поглинання газу рідиною, тобто процес, при якому речовина переходить з газової фази в рідку і розчиняється в ній. Зворотний процес видалення з рідини розчиненого в ній газу називається десорбцією.

Перегонка і ректифікація — розділення гомогенних рідких сумішей шляхом випаровування компоненту, що володіє вищою летючістю, з подальшою конденсацією цього компоненту.

Екстракція — витягання речовини, що знаходиться в твердому тілі або розчиненого в рідині, за допомогою рідини, в якій розчиняється витягувана речовина.

Адсорбція — поглинання твердим пористим поглиначем одного компоненту з багатокомпонентної суміші газів, пари або рідин. Зворотний процес називається десорбцією і служить для виділення адсорбованої речовини і регенерації поглинача.

Сушка — видалення вологи з твердих тіл або рідких середовищ шляхом випаровування.

Кристалізація — виділення одного або декількох компонентів у вигляді кристалів з розчину.

Всі гетерогенні процеси масопередачи включають стадії перенесення речовини в межах однієї фази, переходу речовини з однієї фази в іншу через поверхню розділу і стадії розподілу речовини в іншій фазі. При розгляді механізму масопереносу через кордон розділу фаз в системах газ — рідина, газ — тверде тіло або рідина — тверде тіло розрізняють центральну частину потоку, або ядро потоку, і дифузійний шар, безпосередньо дотичний з поверхнею.

В більшості випадків массообменные процеси супроводжуються теплообміном, який робить вплив на їх швидкість.

Швидкість массопередачи при заданій температурі залежит від інтенсивності молекулярної дифузії, тобто здатності однієї речовини мимоволі проникати в інше за рахунок безладного теплового руху молекул. У рухомому середовищі масопередача може здійснюватися також за рахунок конвективного перенесення маси. Сумарний процес, який складається з молекулярної дифузії і конвективного перенесення, носить назву конвективної дифузії.

Склад речовини необхідно знати для визначення напряму і швидкості массообменного процесу. Його виражають в масових відсотках (мас.%) і масових долях або частіше в молярних відсотках (мовляв.%) або долях. Якщо розглядати суміш, що складається з двох компонентів, — А і В, і прийняти, що

а — масовий відсоток легколетучего компоненту А,

b = 1 — а — масовий відсоток компоненту В

М_А — молекулярна маса компоненту А,

М_В — молекулярна маса компоненту В

Х_а — молекулярна частка легколетучего речовини А в розчині, то зв'язок між масовими а, b і молярними ХА і Хb долями компонентів виражається формулами: 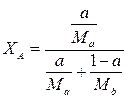(11.1) 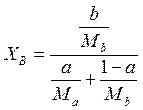(11.2)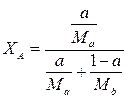

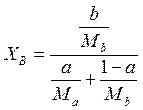
Чисельник визначає число мілі компонентів А і В, а знаменатель—сумму мілі двох речовин. Формули дозволяють розрахувати відношення числа мілі речовин А і В до загального числа мілі, тобто виражають склад в долях благаючи.

Процес перенесення маси з однієї фази в іншу здійснюється до тих пір, поки у фазах не будуть досягнуті умови рівноваги. Умови рівноваги визначаються граничними, або рівноважними, концентраціями, при яких не відбувається переходу речовини з фази у фазу, тобто рушійна сила процесу стає рівною нулю. В умовах рівноваги концентрація розподіленої речовини в одній фазі відповідає строго певній концентрації в іншій фазі. Рівноважні концентрації розраховують за допомогою рівняння рівноваги або визначають по графіку лінії рівноваги.

Перенесення розподілюваної речовини походить завжди з фази, де його зміст вище рівноважного, у фазу, в якій концентрація цієї речовини нижче рівноважною. Так, в процесі абсорбції розподілювана речовина переходить з газової фази в рідку. У процесах перегонки і ректифікації двухкомпо-нентной змішай більш летючу речовину переходить з рідкої фази в парову до тих пір, поки не наступить рівновага між фазами за змістом цього компоненту.

Рівняння массопередачи виражає залежність між кількістю речовини М, передаваного з однієї фази в іншу, поверхнею розділу фаз F і тривалістю процесу ф:

M = KFДф (11.3)

де К — коефіцієнт массопередачи; Д — середня рушійна сила процесу.

Коефіцієнт массопередачивиражає кількість речовини, переданої з однієї фази в іншу, через одиницю поверхні контакту фаз при одиниці рушійної сили процесу за одиницю часу:

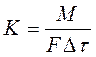(11.4)

1.1. Молекулярна дифузія. У газах і рідинах молекули речовини перебувають у стані хаотичного (теплового) руху. Можна обчислити середню відстань, яку молекула могла б пройти протягом певного відрізку часу, але точно завбачити її шлях і положення неможливо.

Межі зони можливого перебування будь-якої молекули являють собою концентричні поверхні, проведені навколо початкового її положення і які з часом збільшуються за розмірами. Через деякий проміжок часу розміри цієї зони стануть сумірними з розмірами апарата, тобто можливість перебування розглядуваної молекули у будь-якій точці апарата буде однаковою.

Аналогічне явище відбудеться, якщо групу (масу) молекул речовини А помістимо в речовину В. Через деякий час вони рівномірно розподіляться між молекулами речовини В в об'ємі всього апарата і концентрація вирівняється. Таке перенесення маси внаслідок хаотичного руху молекул називають молекулярною дифузією.

Помістимо в посудину з чистою водою кристал солі. Молекули солі перейдуть у розчин і внаслідок хаотичного руху поширюватимуться в об'ємі посудини. Навколо кристала утвориться поле концентрацій. Сполучаючи точки поля з однаковою концентрацією, дістанемо ряд ізоконцентраційних поверхонь, що розміщуються навколо кристала, причому в міру віддалення від нього рівень концентрації зменшується (рис. 1.). У напрямі нормалі до ізоконцентраційної поверхні зміна концентрації на одиницю довжини (градієнт концентрації 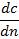) досягає максимального значення.

Німецький вчений А. Фік установив, що при постійних температурі й тиску швидкість молекулярної дифузії пропорційна градієнту концентрацій, узятому з протилежним знаком:

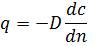, (1.8)

де D — коефіцієнт пропорційності, названий коефіцієнтом молекулярної дифузії, м2/с.

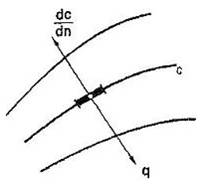
Рисунок 1. До визначення градієнта концентрацій

Це кінетичне рівняння усталеної молекулярної дифузії називають першим законом Фіка. Знак мінус означає, що напрямок дифузійного потоку протилежний градієнту концентрації. Закон Фіка справедливий лише для систем з од­ним градієнтом концентрацій. До таких систем належать бінарні й багатокомпонентні з однаковими бінарними коефіцієнтами всіх пар речовин. При цьому вважається, що потік одного компонента бінарної суміші компенсується зустрічним потоком другого компонента і коефіцієнти дифузії для обох потоків однакові.

Коефіцієнт молекулярної дифузії за­лежить від властивостей дифундуючої речовини, температури, тиску (для газів) і концентрації. Вплив останнього фактора проявляється в основному при високих концентраціях у рідких середовищах. У газовій фазі коефіцієнт молекулярної дифузії становить: (1...10) • 10-5 м2/с. У рідкій фазі дифузія відбувається значно повільніше і коефіцієнт дифузії на чотири порядки нижчий. Коефіцієнт молекулярної дифузії характеризує властивість системи і звичайно його беруть з таблиць, проте у ряді випадків, в основному для газової фази, його можна обчислити.

Обчислення ґрунтується на залежності, встановленій молекулярнокінетичною теорією газів

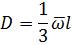, (1.9)

де — середня квадратична швидкість молекул, м/с; l — довжина вільного пробігу молекул.

Найпоширеніше розрахункове рівняння Джілліленда

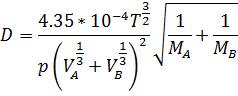, (1.10)

де Т - абсолютна температура, К; р — загальний тиск, Па; VA i VB - молярні об’єми газів А і В м3/кмоль; МА і МВ— молярні об'єми газів А і В, кг/моль.

Рівняння (1.11) дає можливість за наявними табличними значеннями D0 (при р0, Т0) розрахувати коефіцієнт дифузіїD для певних умов (р, Т):

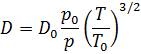, (1.11)

Слід зазначити, що показник степеня при температурі в рівняннях (1.10) і (1.11), визначений на основі молекулярно-кінетичної теорії, не завжди відповідає дослідним даним, за якими він змінюється у межах 1, 5...2, 2 (залежно від природи газів).

Закономірності молекулярної дифузії в рідинах вивчені значно менше, ніж у газах, і розрахунки коефіцієнта дифузії дають дуже наближені значення.

Відоме теоретичне рівняння Стокса — Ейнштейна

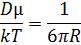, (1.12)

де μ — коефіцієнт динамічної в'язкості розчину, Па • с; k — стала Больцмана, Дж/К; Т — абсолютна температура, К;R — радіус молекул розчиненої речовини, м.

Рівняння (1.12) використовують для визначення коефіцієнта молекуляр­ної дифузії D в рідині при значеннях Т і μ, що відрізняються від умов (Т0, μ0), для яких відомо табличне значення D0:

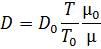, (1.13)

1.2. Конвективна дифузія. Конвективна дифузія — це перенесення маси в рухомому середовищі, яке у разі ламінарного руху відбувається двома потоками: потоком молекулярної дифузії, питоме значення якого qмол визначають за рівнянням (1.8), і потоком речовини разом із середовищем у процесі його руху з питомим значенням

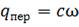, (1.14)

де с — концентрація речовини, кг/м3; ω — швидкість руху середовища.

Швидкість конвективної дифузії дорівнює сумі цих питомих потоків:

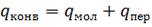, (1.15)

Внаслідок перенесення речовини в елементарному об'ємі dV концентрація змінюється в часі зі швидкістю 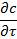, що компенсує дивергенцію векторного поля qконв:

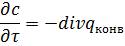, (1.16)

Якщо в процесі хімічних або фазових перетворень у розглядуваний об'єм додатково вводять (або виводять) речовину, тобто є джерело (або витік) речовини, то праву частину рівняння (1.16) треба доповнити складовою Іv, що визначає кількість речовини, яку вводять (або виводять) в одиницю об'єму за одиницю часу:

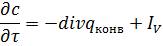, (1.17)

Для усталеного потоку нестисливої рідини і при постійному коефіцієнті дифузії диференціальне рівняння конвективної дифузії (1.17) набуває ви­гляду

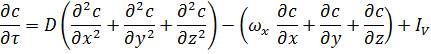, (1.18)

Ліва частина рівняння характеризує зміну поля концентрації в часі, а права — відповідно молекулярну дифузію, конвективне перенесення маси в рухомому середовищі і дію джерел (витоків) речовини.

Рівняння конвективної дифузії істотно спрощується:

а) якщо концентраційне поле незмінне в часі (усталений масообмін), то

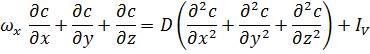, (1.19)

в) якщо середовище нерухоме і немає хімічних перетворень, то

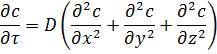, (1.20)

Це рівняння нестаціонарної молекулярної дифузії іноді називають другим законом Фіка.

Наведені вище рівняння конвективної дифузії справедливі для ламінарного потоку.

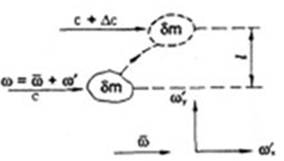
Рисунок 2. Схема турбулентних пульсацій

Проте на практиці, з метою інтенсифікації технологічних процесів, часто вдаються до турбулентних режимів руху середовища. У турбулентному потоці швидкість руху безперервно змінюється в часі, хаотично пульсуючи близько якогось середнього значення , і може бути подана як сума цієї середньої швидкості та пульсуючої складової ω'. Внаслідок турбулентних пульсацій (рис. 2.) макроскопічне скупчення частинок речовини δm переноситься у потоці в різних напрямках, у тому числі й поперек потоку. Пройшовши деякий шлях перемішування l, скупчення частинок δm внаслідок молекулярного перенесення втрачає свою індивідуальність, змішуючись із середовищем. Цей шлях називають також масштабом турбулентних пульсацій.

Перенесення речовини хаотичними турбулентними пульсаціями (турбулентна дифузія) багато в чому аналогічне молекулярній дифузії: масштаб турбулентних пульсацій l є аналогом довжини вільного пробігу молекул, а пульсаційна швидкість ω' — середньої квадратичної швидкості руху моле­кул. Відмінність полягає в тому, що в турбулентному потоці діють не окремі молекули, а умовні групи молекул δт, охоплені загальним для них рухом. Ці групи не мають цілком певних розмірів і швидкості й розпадаються у процесі руху.

За аналогією з молекулярною дифузією питомий потік турбулентної ди­фузії

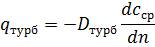, (1.21)

де – Dтурб – коефіцієнт турбулентної дифузії, м2/с, 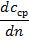- градієнт середньої концентрації кг/(м3·м).

Коефіцієнт турбулентної дифузії — це фізична константа, яка залежить від швидкості турбулентних пульсацій і їхнього масштабу:

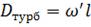, (1.22)

У потоці з розвиненою турбулентністю Dтурб -, значно (в сотні тисяч разів) перевищує коефіцієнт молекулярної дифузії і масоперенесення відбувається дуже інтенсивно. Проте значення Dтурб зменшується в міру наближення до поверхні контакту фаз і біля самої поверхні стає меншим, ніж D.

Щоб розрахувати конвективну дифузію при турбулентному режимі руху середовища, можна використати рівняння конвективної дифузії в ламінарно­му потоці (1.17) і (1.18), складені для осереднених у часі значень швид­кості й концентрації турбулентного потоку, причому замість D треба ввести ефективний коефіцієнт дифузії Dеф = D + Dтурб. На жаль, практичне викори­стання цих рівнянь утруднене через складність визначення Dтурб.

1.3. Масопередача. Перенесення маси в межах однієї фази до межі поділу фаз або від неї називають масовіддачею, а загальний процес перенесення маси з однієї фази в іншу — масопередачею. Закономірності масопередачі визначаються влас­тивостями фаз, що беруть участь у процесах.

У рухомих фазах (рідкій і газовій) маса переноситься дифузією всіх видів.

Всередині пор твердої фази діє, як правило, лише механізм молекуляр­ної дифузії. При цьому швидкість перенесення залежить від пористості твер­дого тіла, геометрії капілярів, співвідношення розмірів капілярів і молекул і характеризується коефіцієнтом масопровідності Dм, пропорційним коефіці­єнту молекулярної дифузії, але меншим від нього за значенням:

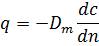, (1.23)

Щоб розрахувати швидкість масовіддачі в газовій або рідкій фазі, потрібно рівняння конвективної дифузії розв'язати спільно з рівнянням руху і нерозривності потоку за заданих граничних і початкових умов. Через надзвичайну складність (неможливість) розв'язання такої системи диференціаль­них рівнянь на практиці використовують рівняння масовіддачі, запропонова­не О. Н. Щукарьовим у кінці XIX ст.:

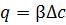, (1.24)

або

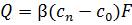, (1.25)

де β — коефіцієнт масовіддачі, м/с; Δс — різниця концентрацій на межі поділу фаз і в ядрі потоку, кг/м3; Q — маса речовини, що розчинюється в одиницю часу, кг/с; сn — концентрація насиченого розчину на межі поділу фаз, кг/м3; с0 — фактична концентрація речовини в центрі потоку на даний момент часу, кг/м3; F — площа міжфазової поверхні, м2.

Одиниця коефіцієнта масовіддачі:

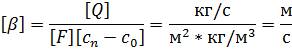, (1.26)

Коефіцієнт масовіддачі показує, яка кількість речовини передається від поверхні поділу фаз у фазу, що сприймає її через 1 м2 поверхні фазового контакту за 1 с при різниці концентрації 1 кг/м3.

Рівняння (1.24) і (1.25) дають можливість усю складність фізичної картини перенесення маси приховати за коефіцієнтом масовіддачі. Завдяки своїй формальній простоті вони мають широке застосування у розрахунковій практиці. Розрахунок коефіцієнтів масовіддачі ґрунтується на теоріях масопередачі.

1.3.1. Теорії масопередачі. Є кілька феноменологічних теорій перенесення маси: плівкова, проникності, оновлення поверхні, міжфазової турбулентності та ін.

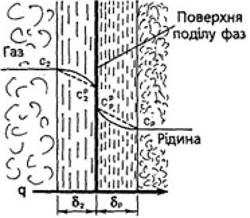
Рисунок 3. Схема примежових плівок біля межі поділу фаз

В основі їх ле­жать різні уявлення (моделі) перенесен­ня маси поблизу поверхні фазового контакту. При цьому звичайно вважають, що опір переходу через поверхню поділу фаз дорівнює нулю і фази перебувають у рівновазі.

Плівкова теорія Нернста. Ця теорія далі була розвинена В. К. Льюісом і В. Д. Уітменом. Вона передбачає існування біля межі поділу фаз примежових плівок завтовшки 8 (рис. 3), в яких маса переноситься виключно завдяки молекулярній дифузії. За межами плівок вступає в дію механізм турбулентної дифузії і маса переноситься настільки інтенсивно, що концентрація в основному потоці вирівнюється, змінення її спостерігається лише в примежових плівках. При постійному градієнті змінення концентрації (штрихові лінії на рис. 3) із рівнянь (1.8) і (1.24)

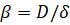, (1.27)

Таке уявлення про примежовий шар досить спрощене.

На думку В. Г. Левича, турбулентний потік має чотиришарову структуру (рис. 4): ядро потоку з розвиненою турбулентністю, турбулентний приме­жовий шар фази δф, в'язкий підшар δ0 і дифузійний підшар δ.

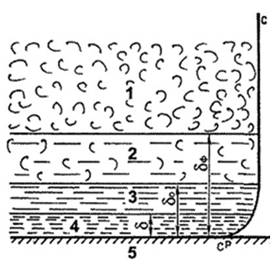
Рисунок 4. Структура турбулентного потоку:

1 - основний потік;

2 - примежовий підшар;

3 - в'язкий підшар;

4 - дифузійний підшар;

5 - тверда фаза

В міру набли­ження до поверхні поділу фаз інтенсивність турбулентних пульсацій поступово падає і в дифузійному підшарі переважає молекулярне перенесення.

Товщина примежової плівки δф залежить від фізико-хімічних властивостей і гідродинамічного стану середовища. З підвищенням турбулентності δф зменшується. Проте плівкова теорія не дає кількісних залежностей для розрахунку δф. Все це утруднює розрахунок коефіцієнта масовід­дачі за рівнянням (1.26). Проте викорис­тання основних положень плівкової теорії в ряді випадків дає позитивні результати.

Експериментальні визначення (за вимі­рюваним значенням потоків Q) показали, що залежність товщини дифузійного підшару δ від швидкості руху потоку се­редовища ω має вигляд:

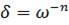, (1.28)

Показник степеня п залежить від умов експерименту. За рекомендацією різних авторів n лежить у межах від 0,5 до 1,0.

Теорія проникності Хігбі. За цією теорією процес конвективної дифузії складається з окремих короткочасних процесів нестаціонарної молекулярної дифузії, що відбуваються під час зіткнення елементів фаз, які взаємодіють. Ці процеси швидко змінюють один одного. Така заміна усталеного процесу конвективної дифузії сукупністю нестаціонарних процесів молекулярної дифузії, що швидко змінюють один одного, за принципом анало­гічно кінозніманню. Тривалість змінення елементів τ довільною величиною, хоч у ряді випадків може мати цілком певний фізичний зміст. Наприклад, у разі рідинної екстракції τ = d/ω, де d - діаметр краплі, м; ω — швидкість руху її відносно суцільної фази, м/с.

За теорією Р. Хігбі,

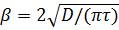, (1.29)

що добре узгоджується з експериментальною залежністю β від D.

Подальшого розвитку теорія проникності набула завдяки ідеї оновлення, яку вперше сформулював у 1937 р. В. М. Стабніков. Суть її полягає в тому, що вирішальну роль у процесі масопередачі відіграє не загальна, а заново утворювана поверхня контакту фаз з елементами, які ще не брали участі в дифузії. Поверхня оновлюється внаслідок проникнення до межі поділу фаз турбулентних вихорів, які оголюють нові шари контактуючих середовищ (що утворюють нові поверхні).

Кількісні залежності теорії оновлення встановлені М. X. Кишинівським і Р. Данквертсом.

За М. X. Кишинівським,

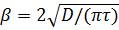, (1.30)

де Dеф = D + Dтурб — ефективний коефіцієнт дифузії.

За Р. Данквертсом,

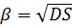, (1.31)

де S — фактор оновлення поверхні, що дорівнює частині поверхні, яка онов­люється протягом одиниці часу.

Плівково-проникна модель, що розроблена X. Л. Туром і Д. М. Марчелло, передбачає різний механізм передавання маси до поверхонь різного віку. У разі тривалого перебування вихору на поверхні контакту (стара поверх­ня) масовіддача описується плівковою моделлю, а в разі короткочасного (нова поверхня) — моделлю оновлення. Якщо є поверхні різного віку, то β~Dn де 0,5 < п < 1,0.

Усі розглянуті теорії масоперенесення — це лише більш-менш вдалі на­ближення (моделі) того складного явища, що існує насправді, і жодна з тео­рій не може вважатися повною. Проте вони дають можливість вкласти певний фізичний зміст у рівняння, які одержують при обробленні експерименталь­них даних, і правильно аналізувати спостережувані явища.

1.3.2. Рівняння масопередачі. Загальне рівняння масопередачі є вираженням основного кінетичного за­кону для процесу перенесення маси

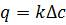, (1.32)

де kк — коефіцієнт масопередачі, що залежить від особливостей перебігу про­цесу у фазах і на межі поділу, м/с; Δс — рушійна сила — різниця діючої і рівноважної концентрацій (з додатним знаком), кг/м3.

Рушійну силу виражають через концентрацію компонента в одній із фаз. Розглянемо це на прикладі масопередачі в системі газ — рідина (див. рис. 3). За виразом (1.24) масопередачу у фазах виражають рівняннями

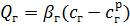, (1.33)

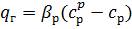, (1.34)

де 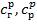— концентрації газової і рідкої фаз на межі поділу, а сг, ср — концентрації фаз в ядрі потоку, кг/м3.

Виразимо рушійну силу в одній із фаз (наприклад, у рідині) через рівно­важні концентрації другої фази (газу), вважаючи, що на межі поділу фаз опору немає і постійно існує рівновага:

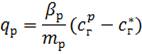, (1.35)

де mр — константа фазової рівноваги; сг* = трср — концентрація газової фази, рівноважна з концентрацією рідкої фази в ядрі потоку, кг/м3.

Розв'язуючи спільно рівняння (1.33) і (1.34) і враховуючи, що потоки маси у фазах і в цілому в системі не змінюються, дістанемо рівняння масопередачі

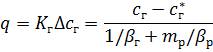(1.36)

де Δсг = сг - сг* — рушійна сила, виражена через концентрації газової фази,

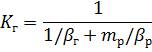(1.37)

коефіцієнт масопередачі, м/с.

Виразивши рушійну силу через концентрацію рідкої фази, дістанемо рівняння масопередачі у вигляді

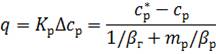, (1.38)

Знаменники у рівняннях (1.36) і (1.37) — це опір масопередачі, що дорівнює сумі опорів газової і рідкої фаз. Цей принцип об'єднання (адитивності) фазових опорів хоч і піддавався неодноразово сумніву, досі є загаль­новизнаним і застосовується не тільки до системи газ — рідина, а й до всіх систем масопередачі.

Аналіз рівняння масопередачі показує, що для добре розчинних газів (mр — мала) весь опір масопередачі концентрується в газовій фазі, тобто Кг≈βг, а для погано розчинних газів (mр — дуже велика) опір масопередачі чинить практично лише рідка фаза Кр≈βр. При середніх значеннях mр опори фаз сумірні, тому К треба розраховувати за загальним рівнянням. Аналогічно діють і при розрахунках масопередачі в інших системах.

Використання наведених вище рівнянь масопередачі для розрахунку про­мислових апаратів утруднюється тим, що коефіцієнт масопередачі та рушій­на сила змінюються вздовж апарата і в його поперечному перерізі. Інженера ж звичайно цікавить середня по апарату продуктивність масо передачі

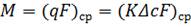, (1.39)

Якщо поверхня контакту фаз F невідома, то в рівняння (1.39) вводять об'ємний коефіцієнт масопередачі Кv = Кf= КF/V, с-1, тобто застосовують , рівняння масо передачі

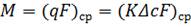, (1.40)

Виражаючи робочий об'єм V через площу поперечного перерізу S та ви­соту Н апарата, дістають розрахункове рівняння масо передачі

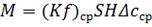, (1.41)

Об'ємний коефіцієнт характеризується масою, що передається в одиниці об'єму апарата протягом одиниці часу при одиничній різниці концентрацій. Змінення рівня об'ємного коефіцієнта масопередачі в межах апарата пов'я­зане насамперед зі зміненням розміру питомої поверхні контакту фаз внаслі­док нерівномірної дисипації енергії в робочому об'ємі. Визначивши значення Кv в окремих елементах об'єму, можна знайти його середнє по апарату зна­чення (Кv)ср. При цьому особливу увагу звертають на зони підвищеної інтен­сивності масопередачі, в яких діють джерела механічної енергії, і застійні зони, де рівні дисипації енергії та інтенсивності масопередачі найнижчі.

Характер змінення Δс і її середнього значення Δсср залежить від макроперемішування (перемішування на рівні поздовжніх розмірів апарата), що створює певну структуру потоків фаз в апараті.

Граничні структури потоків відомі як моделі ідеального витіснення та іде­ального перемішування. При ідеальному витісненні немає поздовжнього перемішування (коефіцієнт поздовжнього перемішування Δl, м2/с, дорівнює нулю), а при ідеальному перемішуванні воно настільки інтенсивне (ΔL =∞), що вирівнює концентрацію в об'ємі апарата (ступені).

Середня рушійна сила Δсср у разі ідеального витіснення найбільша і за умови прямолінійності рівноважної залежності її розраховують як середньо-логарифмічну

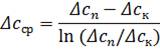, (1.42)

де Δсn Δск — початкова і кінцева рушійні сили.

Ідеальне перемішування стабілізує рушійні сили в апараті на найнижчо­му рівні: Δсср = Δск.

У реальних умовах середня рушійна сила лежить між цими крайніми її значеннями і залежить від структури потоків, яку характеризують критерієм Пекле для поздовжнього перемішування Ре_L = ωН/D_L, де ω — середня швидкість потоку, м/с, Н - висота (довжина) апарата, м. При ідеальному витісненні Ре_L=∞ а при ідеальному перемішуванні Ре_L= 0.

Наявність в апараті зон підвищеної інтенсифікації внаслідок дії джерел механічної енергії і застійних зон ускладнює розрахунок Δс_ср. Так, у зонах підвищеної інтенсивності масопередачі завдяки потужному мікроперемішуванню (на рівні частинок дисперсної фази) зростає робоча концентрація і знижується рушійна сила, що зменшує ефективність інтенсифікації, незважаючи на високий рівень Ку.

Коефіцієнт корисної дії джерела інтенсифікації підвищують за допомогою додаткового перемішування на рівні розмірів зони чи поперечного розміру апарата, яке вирівнює концентрацію і збільшує рушійну силу, тобто завдяки раціональному розподілу механічної енергії по рівнях перемішування.

За рівнянням (1.41) апарати розраховують трьома способами:

· за середніми значеннями об'ємного коефіцієнта масопередачі (Кv)с і рушійної сили Δсср;

· за висотою і числом одиниць перенесення маси (ВОП і ЧОП);

· за висотою і кількістю теоретичних ступенів змінення концентрації.

Усі три способи теоретично рівнозначні, і вибір того чи іншого з них визначається практичними міркуваннями.

Поняття висоти одиниці перенесення (ВОП) і числа одиниць перенесен­ня (ЧОП) можна встановити, розв'язуючи разом з рівнянням (1.41) ще рівняння матеріального балансу речовини, яку передають в одній із фаз (на­приклад, газовій),

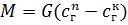, (1.43)

де G – витрата газу; 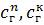- початкова і кінцева концентрації газу, кг/м3.

Отже дістанемо:

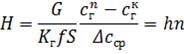, (1.44)

де 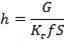- висота одиниці перенесення маси; 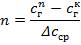- число одиниць перенесення маси.

Одиниця перенесення маси — це елементарний об'єм апарата заввишки Н, в якому зміна концентрації в одній із фаз дорівнює середній рушійній силі в межах цього елемента. Висоту одиниці перенесення Н, як і Кv, ви­значають експериментально.

Число одиниць перенесення маси для прямолінійної форми лінії рівноваги (mр = const) визначають графічно побудовою ступенів концентрації, а для криволінійної форми — графічним інтегруванням рівняння

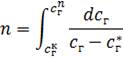, (1.45)

Метод теоретичних ступенів змінення концентрації аналогічний описаному вище. Відмінність лише у тому, що за розрахункові елементи об'єму апа­рата взято не одиниці перенесення, а теоретичні ступені змінення концентрації (теоретичні тарілки), в яких на виході досягається концентрація, що дорівнює рівноважній концентрації на вході. Кількість теоретичних ступенів змінення концентрації визначають графічною побудовою ступенів концентрації між робочою лінією і лінією рівноваги (див. процес ректифікації), а висоту апарата, еквівалентну теоретичному ступеню (ВЕТС), — експеримен­тально, виходячи з ефективності роботи апарата. Висота апарата дорівнює добутку ВЕТС на кількість теоретичних ступенів змінення концентрації.

Розраховуючи масообмінні апарати, що в дійсності складаються з окре­мих елементів (тарілок), ефективність яких нижча за теоретичний ступінь змінення концентрацій (теоретичну тарілку), поряд з кривою рівноваги іноді будують кінетичну криву, що характеризує змінення концентрації, якого до­сягають на реальних тарілках. Здійснюючи графічну побудову ступенів кон­центрації між робочою лінією і кінетичною кривою, визначають справжню кількість тарілок.

Щоб розрахувати апарати за будь-яким з розглянутих способів, треба знати величину, що характеризує кінетику процесу (К, Кv, ВОП, ВЕТС, кінетичну криву). Ці величини визначають експериментально, використовуючи теорію подібності.

Як видно з рівнянь масопередачі, інтенсифікації дифузійних процесів можна досягти як збільшенням коефіцієнтів масопередачі К, Кv (зменшенням ВОП і ВЕТС), так і збільшенням середньої рушійної сили. Одним з найпоширеніших способів інтенсифікації є турбулізація фаз, яка сприяє збільшенню поверхні контакту фаз і активізує поверхню завдяки швидкому оновленню.

1.4. Поняття про термодифузію. Розглянуті вище основні закони дифузії встановлені за умови дії лише однієї рушійної сили градієнта концентрацій розглядуваного компонента системи. В реальних умовах масопередачі є звичайно і градієнти інших інтенсивних параметрів: температури, тиску, концентрації решти компонентів системи. Встановлено, що швидкість дифузії даного компонента більшою чи меншою мірою залежить також від усіх зазначених градієнтів. Так, для молекулярного перенесення в бінарній суміші можна записати

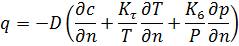(1.54)

де Kт — термодифузійний коефіцієнт; К6 — бародифузійний коефіцієнт.

У цьому рівнянні перша складова величина характеризує концентраційну дифузію, друга — термодифузію (ефект Соре), третя — бародифузію. Звичайно бародифузією нехтують. Що ж до термодифузії, то вона у ряді випадків відіграє помітну роль (наприклад, у процесах сушіння матеріалів). Коефіцієнт термодифузії додатний для важчих компонентів і від'ємний — для легших. Отже, важкі компоненти переміщуються в бік зниження температури.

Дія термодифузії проявляється переважно в газах і до деякої міри в рідинах. Проектуючи апарати, треба прагнути, щоб напрямки термодифузії і кон­центраційної дифузії збігались.

1.5. Подібність дифузійних процесів. Потреба у використанні теорії подібності дифузійних процесів виникла у зв'язку з тим, що аналітичне розв'язання системи диференціальних рівнянь які виражають процес перенесення маси в технологічних апаратах, поки ще неможливе. Тому методом подібного перетворення з цієї системи дістають критерії дифузійної подібності, а експериментальні дані з масовіддачі в промислових апаратах та їхніх моделях подають у вигляді узагальнених (критеріальних) залежностей, з яких потім визначають шукану величи­ну — коефіцієнт масовіддачі. Подібне перетворення рівняння конвективної дифузії (1.18) дає дифузійний критерій Фур'є, що характеризує змінення швидкості дифузії у часі:

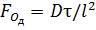, (1.46)

і дифузійний критерій Пекле

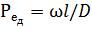, (1.47)

який записують у вигляді

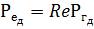, (1.48)

де Ргд = V/D — дифузійний критерій Прандтля, що характеризує подібність полів фізичних величин і визначається лише фізичними властивостями середовища.

З рівняння граничних умов визначають дифузійний критерій Нуссельта

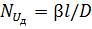, (1.49)

а для систем з твердим тілом — дифузійний критерій Біо

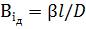, (1.50)

де Dм - коефіцієнт масопровідності.

Дифузійний критерій Нуссельта — це відношення швидкості конвективного перенесення маси у потоці до швидкості молекулярного перенесення в примежовому шарі. Цей критерій містить шуканий коефіцієнт масовіддачі, і він визначуваний.

У дифузійному критерії Від швидкість конвективного перенесення порівнюється зі швидкістю молекулярного перенесення всередині твердого тіла. При великих значеннях Від процес лімітується перенесенням всередині тіла (внутрішнє масоперенесення), а при малих Від — перенесенням у навколиш­ньому середовищі (зовнішній масообмін).

Узагальнені (критеріальні) рівняння масовіддачі мають вигляд

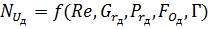, (1.51)

де Grд — критерій Грасгофа, що враховує дію природної конвекції внаслі­док різниці концентрацій: Grд = Gr(ρn –ρ)/ρ; рn — густина насиченого роз­чину; ρ — густина середовища; Г — симплекс геометричної подібності. Для систем з твердою фазою користуються узагальненою залежністю

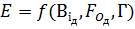, (1.52)

де Е - безрозмірний симплекс концентрацій, що набуває різних виразів залежно від умов масопередачі.

У конкретних випадках масообміну критеріальні рівняння (1.49) і (1.50) спрощуються. При стаціонарному масообміні випадає критерій Fод; у разі інтенсивного вимушеного руху і малих Δс можна знехтувати Grл; симплекс геометричної подібності враховують при моделюванні процесу, але його часто немає в розрахункових рівняннях.