Лучистый теплообмен между двумя параллельными пластинами

Рассмотрим две параллельные пластины единичной площади, между которыми происходит лучистый теплообмен. Будем считать, что T₁>Т₂ и пластины непрозрачны для излучения (т. е. D=0).

Рассмотрим (рис. 13.7), как расходуется энергия, излучаемая этими телами. Первая пластина излучает энергию E₁. Достигнув поверхности второй пластины, часть этой энергии E₁A,а другая часть (1–A₂)E₁ отразится от поверхности и вновь достигнет первой пластины. Затем часть энергии А₁(1–A₂)E₁ будет поглощена, а часть А₁(1–A₂)(1–A₁)E₁ отразится. И в дальнейшем этот процесс будет продолжаться, постепенно затухая. Аналогично происходит и с энергией Е₂ излучаемой второй пластиной.

Для того чтобы определить величину лучистого теплового потока через плоскость, расположенную между этими пластинами, надо вычислить баланс энергии для каждой пластины. Аналогичную задачу мы решали при выводе закона Кирхгофа. Но такое суммирование бесконечного числа постепенно затухающих потоков энергии можно упростить. Введем для этого понятие эффективного излучения Е_эф.

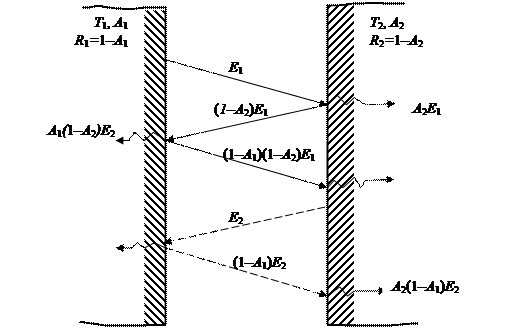
Рис. 13.7. Лучистый теплообмен между двумя параллельными пластинами

Сумма потоков собственного и отражаемого телом излучения называется его эффективным излучением

Е_эф=Е_изл+R∙Е_пад, (13.17)

т.е. Е_эф — это полное излучение, исходящее от тела.

С учетом того, что для непрозрачных тел R=1–A, для каждой пластины согласно (13.17) можно записать, что

Е_эф.1=Е₁+(1–A₁)Е_пад; Е_эф.2=Е₂+(1–A₂)Е_пад. (13.18)

Тогда для первой пластины Е_эф.1 будет расходной (уходящей) энергией, а Е_эф.2 — приходящей. Следовательно, результирующий поток от первой (более горячей) пластины ко второй определится следующим образом:

q_л=Е_эф.1–Е_эф.2. (13.19)

Решая систему уравнений (13.13) относительно Е_эф.1 получим

Е_эф.1=Е₁+(1–A₁)[Е₂+(1–A₂)Е_эф.2]. (13.20)

или

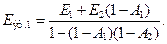
Аналогично

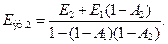(13.21)

Подставим (13.20) и (13.21) в (13.19), получим

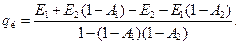
Окончательно после сокращений в знаменателе

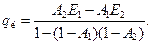(13.22)

Но согласно закону Стефана-Больцмана

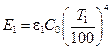и

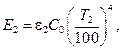
а по закону Кирхгофа e=A₁ и e₂=A₂. С учетом этого выражение (13.22) принимает вид

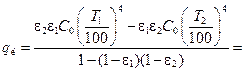
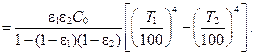
Величину

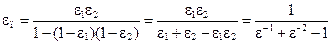
называют приведенной степенью черноты системы двух тел.

Окончательно

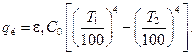(13.23)

Заметим, что в приближенных расчетах можно пользоваться формулой ε_пр=ε₁ε₂. При этом в случае, если ε₁ и ε₂>0,8, ошибка не превышает 20%.