Сила гидростатического давления на плоские поверхности.
Пусть в сосуде боковая плоскость которого наклонена под углом 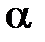 к горизонту, заключена находящаяся в равновесии жидкость, плотность которой
к горизонту, заключена находящаяся в равновесии жидкость, плотность которой 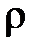 . Давление на свободной поверхности жидкости
. Давление на свободной поверхности жидкости 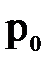 .
.
В пределах боковой стенки имеется плоская фигура произвольной формы, силу давления на которую необходимо определить. Для удобства рассуждений мысленно повернем боковую стенку сосуда и совместим с плоскостью чертежа. Выберем начало координат в месте пересечения поверхности жидкости со стенкой, а ось х будем считать направленной нормально к плоскости чертежа.
Рассмотрим в пределах интересующей нас плоской фигуры произвольную точку А, находящуюся на глубине h под поверхностью жидкости, находящуюся от оси х на расстоянии 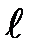 . Выделим у этой точки элементарную площадку площадью
. Выделим у этой точки элементарную площадку площадью 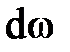 . Тогда элементарная сила; действующая на эту площадку,
. Тогда элементарная сила; действующая на эту площадку, 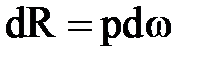 ,где p- абсолютное гидростатическое давление в точке А,
,где p- абсолютное гидростатическое давление в точке А, 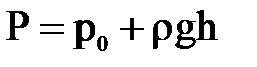 , или
, или 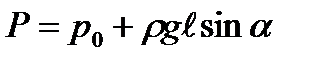 .
.
Искомая сила абсолютного гидростатического давления, действующая на рассматриваемую плоскую поверхность, 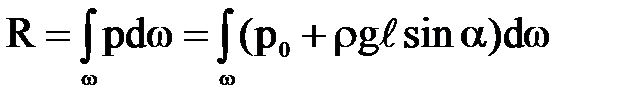 .
.
Считая, что в рассматриваемых условиях 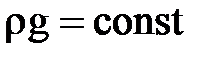 получим
получим 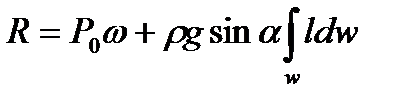
Как известно из теоретической механики, 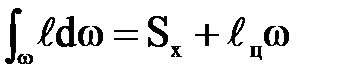
Где 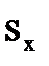 - статический момент плоской фигуры относительно оси х. Следовательно,
- статический момент плоской фигуры относительно оси х. Следовательно,
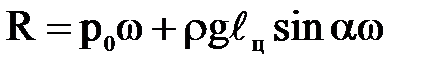 .
.
Учитывая, что 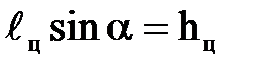 ,
,
где 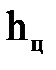 - глубина погружения центра тяжести смоченной части плоской поверхности, получим
- глубина погружения центра тяжести смоченной части плоской поверхности, получим 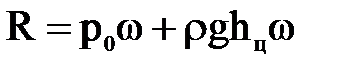 , или после выноса за скобки площади рассматриваемой фигуры ω, будем иметь
, или после выноса за скобки площади рассматриваемой фигуры ω, будем иметь 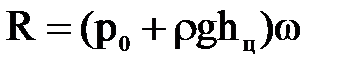 .
.
Таким образом, сила абсолютного гидростатического давления жидкости на погруженную плоскую поверхность равна произведению площади этой поверхности на давление в ее центре тяжести.
При этом сила внешнего гидростатического давления 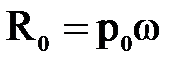 , поскольку внешнее гидростатическое давление
, поскольку внешнее гидростатическое давление 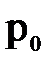 распределено равномерно по всей площади смоченной части поверхности, его равнодействующая
распределено равномерно по всей площади смоченной части поверхности, его равнодействующая  приложена в центре тяжести этой поверхности.
приложена в центре тяжести этой поверхности.
Сила избыточного гидростатического давления 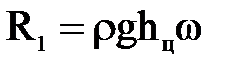 .
.
В случае, когда стенка расположена горизонтально (угол α=0 ),т.е. представляет собой не боковую стенку, а горизонтальное дно сосуда, суммарное давление определяется по тем же формулам и составляет 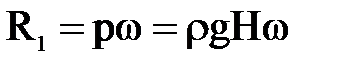 , где H- высота столба жидкости в сосуде.
, где H- высота столба жидкости в сосуде.
Следовательно, давление на дно не зависит не от формулы и объема сосуда, а только от площади дна и высоты столба жидкости в сосуде. Поэтому для сосудов разной формы заполненных одной и той же жидкостью до одного и того же уровня и имеющих одинаковую площадь дна, силы полного давления на дно будут одинаковы.
Это явление, на первый взгляд противоречащее обычным представлениям, впервые подмечено французским физиком Б.Паскалем, носит название гидростатического парадокса.
Эпюры нормальных гидростатических напряжений.
В ряде случаев полное давление на плоскую стенку можно определить графическим способом. Для этого строят эпюры нормальных гидростатических напряжений.
Эпюрой нормальных гидростатических напряжений называется графическое изображение закона распределения нормального гидростатического напряжения по рассматриваемой поверхности.
Рассмотрим построение эпюры нормальных гидростатических напряжений на вертикальную стенку, уровень жидкости перед которой H (а)
Внешнее гидростатическое давление  равномерно передается жидкости по всему ее объему. Отложив в масштабе
равномерно передается жидкости по всему ее объему. Отложив в масштабе 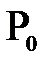 на перпендикулярах к рассматриваемой плоской стенке в ее верхней и нижней части и соединив концы векторов прямой линией получим прямоугольник -эпюру нормальных напряжений вызываемых внешним давлением. Избыточное гидростатическое давление изменяется с глубиной по закону прямой, причем оно равно 0 на свободной поверхности жидкости и максимально у дна-
на перпендикулярах к рассматриваемой плоской стенке в ее верхней и нижней части и соединив концы векторов прямой линией получим прямоугольник -эпюру нормальных напряжений вызываемых внешним давлением. Избыточное гидростатическое давление изменяется с глубиной по закону прямой, причем оно равно 0 на свободной поверхности жидкости и максимально у дна- 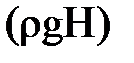
Таким образом, эпюры нормального избыточного гидростатического напряжения имеют форму прямоугольного треугольника (в)
Эпюра нормального абсолютного гидростатического напряжения получается в результате сложения предыдущих двух эпюр и имеет форму трапеции.
Аналогично строятся эпюры нормального гидростатического напряжения в случае наклонной стенки.
Центр давления.
Центром давления называется точка приложения равнодействующей силы избыточного давления.
Рассмотрим произвольную плоскую фигуру, лежащую внутри жидкости в пределах боковой наклонной поверхности под углом α к горизонту. Выберем начало координат на свободной поверхности жидкости в месте ее пересечения с боковой стенкой, ось х считаем горизонтальной и направленной нормально к плоскости чертежа.
Для удобства рассмотрения мысленно совместим боковую стенку с плоскостью чертежа. Выделим в пределах рассматриваемой плоской фигуры произвольную точку А с координатой х, находящуюся на глубине h под свободной поверхностью жидкости и отстоящую от оси х на расстоянии 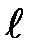 .
.
Поскольку избыточное гидростатическое давление в рассматриваемой точке 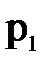 , элементарная сила избыточного давления, действующая на элементарную площадку
, элементарная сила избыточного давления, действующая на элементарную площадку 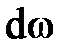 , выделенную вокруг этой точки,
, выделенную вокруг этой точки,
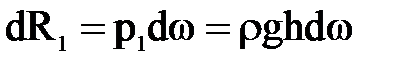 .
.
Элементарный момент этой силы относительно оси х
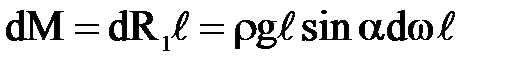 .
.
Тогда суммарный момент силы избыточного давления, действующей на рассматриваемую плоскую поверхность,
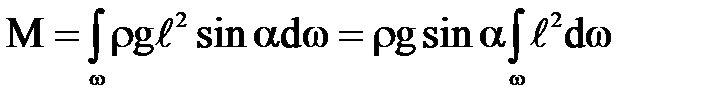 (2)
(2)
Из теоретической механики известно, что
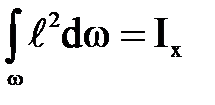 , (3)
, (3)
где  - момент инерции плоской фигуры относительно оси х.
- момент инерции плоской фигуры относительно оси х.
Но тот же момент силы
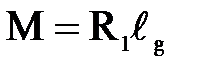 (1)
(1)
где 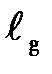 - расстояние от оси х до точки приложения силы избыточного давления то есть искомая координата центра давления.
- расстояние от оси х до точки приложения силы избыточного давления то есть искомая координата центра давления.
Сила избыточного давления
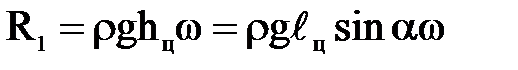 .
.
Подставляя в (1) с учетом (2) и (3), получим
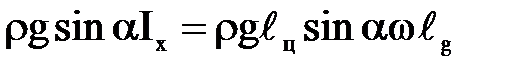 .
.
Откуда 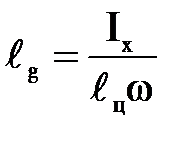 (5)
(5)
Момент инерции относительно горизонтальной оси, параллельной оси, проходящей через центр тяжести фигуры,
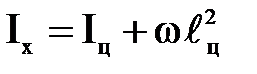 , (4)
, (4)
где 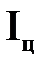 - момент инерции плоской фигуры относительно центральной оси.
- момент инерции плоской фигуры относительно центральной оси.
Подставляя (4) в (5) получим

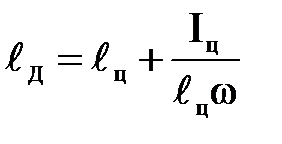 .
.
Таким образом, центр давления лежит ниже центра тяжести плоской фигуры на величину
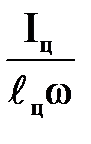 .
.
Центр тяжести и центр давления могут совпадать только тогда, когда рассматриваемая плоская поверхность лежит в горизонтальной плоскости (в этом случае 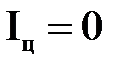 )
)
Зная силы 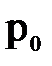 и
и 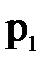 и координаты точек приложения
и координаты точек приложения 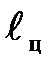 и
и 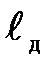 , по правилу сложения параллельных сил нетрудно определить равнодействующую этих сил
, по правилу сложения параллельных сил нетрудно определить равнодействующую этих сил
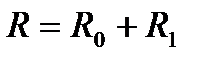 , и точку приложения.
, и точку приложения.
Моменты инерции 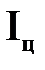 для наиболее распространенных плоских фигур :
для наиболее распространенных плоских фигур :
для квадрата со стороной а
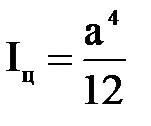 ;
;
для прямоугольника шириной В и высотой H
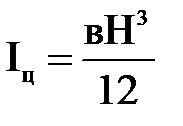 ;
;
для круга диаметром d
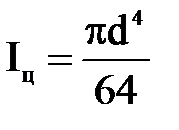 .
.
Дата добавления: 2016-06-15; просмотров: 4159;











