Двухсекторная модель стратегии спроса

Факториальные модели стратегии спроса

Пример 1. Предположим, имеются данные, характеризующие изменения спроса (у) в зависимости от двух факторов: х (цена), z (насыщенность потребительского рынка).

у_(спрос) {29,4; 29,9; 30,1; 30,4; 30,9; 31,4};

х_(цена){28,3; 31,2; 33,5; 36,4; 37,5; 38,8};

z_{(н. р.)} {84,5; 85,6; 86,9; 87,8; 89,5; 90,8}.

Требуется предвидеть, как изменится спрос в будущем, если тенденция сохранится? Насыщенность потребительского рынка не превышает 85%.

Данные дают основания утверждать, что спрос возрастает, уровень роста составляет 6,8%. Возрастают цены, а также насыщенность потребительского рынка, хотя насыщенность рынка не превышает 100%.

Есть основания полагать, что данная зависимость носит прямо пропорциональный характер следующего вида:

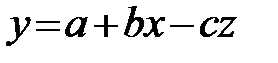Составляем систему стандартных уравнений:

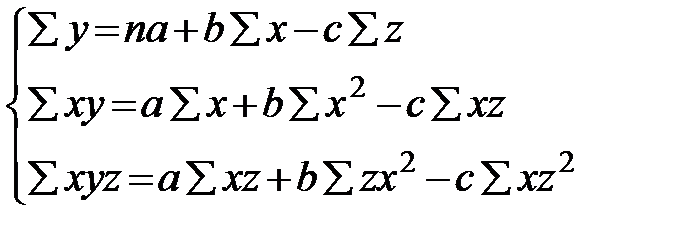
Для решения системы также составляем рабочую таблицу.

Для расчета параметров системы стандартных уравнений

№ пп	у	х	z	x²	z²	xy	xz	xyz	zx²	xz²	y²	z²y
	29,4	28,3	84,5	800,89	7140,25	832,02	2391,35	70305,69	67675,265	202069,08	864,36	2484,3
	29,9	31,2	85,6	973,77	7327,36	932,88	2670,72	79854,528	23326,464	228613,63	894,01	2559,44
	30,1	33,5	86,9	1122,25	7551,61	1008,35	2911,15	87625,615	97523,525	252978,94	906,01	2615,69
	20,4	36,4	87,8	1324,96	7708,84	1106,56	3195,92	97155,968	116331,49	280601,78	924,16	2669,12
	30,9	37,5	89,5	1406,25	8010,25	1158,75	3356,25	103708,13	125859,38	300384,38	954,81	2765,55
	31,4	38,8	90,8	1505,44	8244,64	1218,32	3523,04	110623,46	136693,95	319892,03	985,96	2851,12
Сумма	182,1	205,7	525,1	7133,23	45982,95	6256,88	18048,43	549273,38	627410,01	1584539,83	5529,31	15945,22

Затем составляем систему стандартных уравнений в количественном отношении:

	182,1 = 6a + 205,7b – 525,1z	: 6
	6256,88 = 205,7a + 7133,23b – 18048,43c	: 205,7
	549273,38 = 18048,43a + 627410,01b –1584539,83c	:18048,43

Получим:

30,35 = а + 34,2833b – 87,5166c (1)

30,4175 = a + 34,6778b – 27,7415c (2)

30,4333 = a + 34,7625b – 87,79993c (3)

(2) – (1)

(2) – (3)

Имеем:

	0,10675 = 0,3945b – 0,2249c	: 0,3945
	-0,0158 = -0,0847b + 0578c	: -0,0847

0,1711 = b – 0,5701c

0,1865 = b – 0,6729c

В итоге, с = -0,18; b = 0,16; а = 29,3.

Имеем, у = 29,3 + 0,16 + 0,18z.

Итак, у_t₍₁₎= 29,3 + 0,16 + 0,18 = 29,64;

у_t₍₂₎= 29,3 + 0,16 ∙ 2 + 0,18∙ 2 = 29,98;

у_t₍₃₎= 30,32; у_t₍₄₎= 30,66

у_t₍₅₎= 31,0; у_t₍₆₎= 31,34.

Таким образом, на основе выявленной функции спрос увеличивается с 29,64 до 31,34, т.е. на 5,7%. В данном случае коэффициент множественной корреляции R_y₍_x_,_z₎= 0,91; D_R = 82,8%.

Вывод. Учитывая неполную насыщенность потребительского рынка с ростом цен, будет иметь место увеличение спроса на 5,7%. Данный вывод является адекватным на уровне 82,8%.

Пример 2. Имеются данные:

у_(спрос) {18,3; 19,4; 20,9; 21,4; 22,3};

х₁_(цена){22,9; 23,4; 24,8; 25,8; 26,4};

х₂_(н.р.){122,9; 123,4; 125,9; 126,8; 127,7}.

Требуется предвидеть дальнейшее поведение спроса.

Решение. Выбираем функцию:

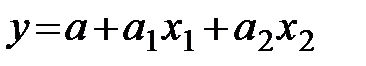Составляем систему стандартных уравнений:

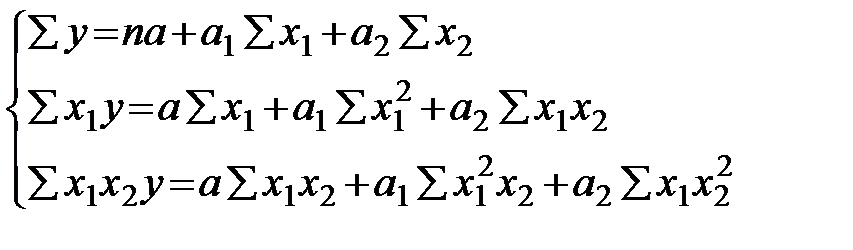
Составляем рабочую таблицу:

	у_(спрос)	х₂_{(емкость)}	х₁_(цена)	ух₁	х₁²	х₁х₂	ух₁х₂	х₂х₁²	х₁х₂²
	18,3	122,9	22,9	419,07	524,41	2814,41	51503,7	64449,99
	19,4	123,4	23,4	453,96	547,56	2887,56	56018,66	67568,9	356324,9
	20,9	125,9	24,8	518,32	615,04	3122,32	65256,49	77433,54	393100,1
	21,4	126,8	25,7	549,98	660,49	3258,76	69737,46	83750,13	413210,8
	22,3	127,7	26,4	588,72	696,96	3371,28	75179,54	89001,79	430512,5
∑	102,3	626,7	123,2	2530,05	3044,46	15454,33	317695,9	382204,4

После решения получим функцию спроса:

у= -75,5352 + 0,0007347х₁ + 0,7737х₂

у_t₁ = 18,57; у_t₂ = 19,56;

у_t₃ = 21,89; у_t₄ = 22,59;

у_t₅= 23,29.

Спрос увеличивается на 6,0%.

Расчет коэффициента множественной корреляции:

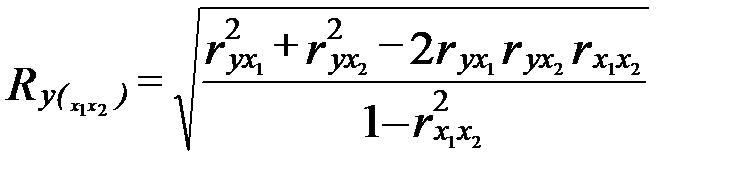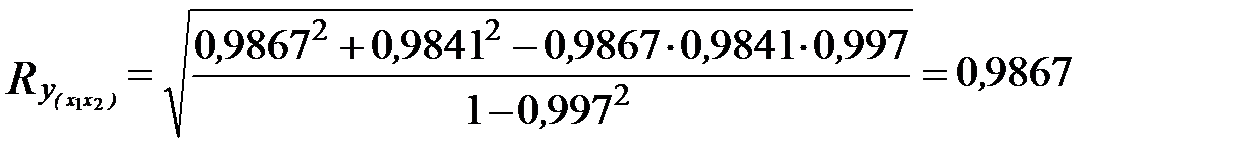
D_R = R²^∙ 100 = 97,3%.

Вывод. Полученные данные позволяют спрогнозировать дальнейшее развитие ситуации на рынке. С достоверностью 97,3% можно утверждать, что при дальнейшем увеличении цены на продукцию спрос будет расти.

Пример 3.Обратно пропорциональная функция спроса в условиях перенасыщенности рынка.

Предположим, имеются данные:

у_(спрос) {39,3; 38,8; 38,1; 37,8; 37,1; 36,8};

х_(цена) {8,7; 8,84; 8,86; 8,96; 9,01; 9,17};

z_(н.р.) {135,8; 141,4; 135,9; 145,5; 139,8; 147,3}.

Нужно предвидеть изменение спроса при сохранении тенденции.

Решение. Анализ данных дает основание утверждать, что спрос снижается, уровень снижения спроса составляет 6,4%; при этом цены на товары возрастают на 5,4%; уровень насыщенности также возрастает.

В данном случае в качестве функции спроса можно выбрать функцию следующего вида:

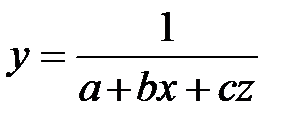где х - цена;

х – насыщенность рынка;

у - спрос;

a, b, с - параметры системы.

Система стандартных уравнений в данном случае имеет вид:

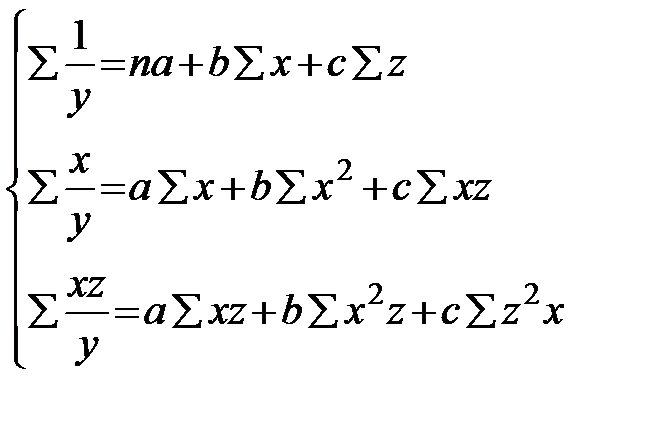
Составляем рабочую таблицу.

№ пп	у	z	х	z ²	у ²	x ²	xz	1 у	х у	хz y	x²z	z²x
	39,3	135,8	8,7	18441,64	1544,49	75,69	1181,46	0,025445	0,221374	30,0626	10278,7	160442,3
	38,8	141,4	8,84	19993,96	1505,44	78.1456	1249,976	0,025773	0,227835	32,21588	11049,79	176746,6
	38,1	135,9	8,86	18468,81	1451,61	78,4996	1204,074	0,026247	0,232546	31,60299	10668,1	163633,7
	37,8	145,5	8,96	21170,25	1428,84	80,2816	1303,68	0,026455	0,237037	34,48889	11680,97	189685,4
	37,1	139,8	9,01	19544,04	1376,41	81,1801	1259,598	0,026954	0,242857	33,95143	11348,98	176091,8
	36,8	147,3	9,17	21697,29	1354,24	84,0889	1350,741	0,027174	0,249185	36,70492	12386,29	198964,1
Сумма	227,9	845,7	53,54		8661,03	477,8858	7549,529	0,158048	1,410834	199,0267	67412,83

Имеем систему уравнений:

0,158048 = 6а – 53,54b + 845,7с

1,410834 = 53,54а - 477,8858b + 7549,529с

199,0267 = 7549,529а – 67412,83b + 1065564с

0,0263413 = а – 8,9233b + 140,95c

0,0263510 = a – 8,9258b + 141,0073c

0,0263628 = a – 8,9294b + 141,1431c

0,0000097 = -0,0025b + 0,0573c

- 0,0000118 = 0,0036b – 0,1358c

0,00388 = -b + 22,92c

0,00328 = b + 37,72c

0,00716 = 60,64c

c = 0,000118073

b = 0,001173766

a = 0,0104738661478 – 0,01664238935 + 0,0263413 = 0,0201073.

Функция спроса имеет вид:

Найдем варианты спроса на основе полученной функции:

у_(х,_z₎₍₁₎ = 38,47; у_(х,_z₎₍₂₎ = 37,75;

у_(х,_z₎₍₃₎ = 38,73; у_(х,_z₎₍₄₎ = 37,26;

у_(х,_z₎₍₅₎ = 38,31; у_(х,_z₎₍₆₎ = 37,31.

В целом спрос снижается. В данном случае D_R = 96%.

Вывод. При постоянно увеличивающейся насыщенности рынка и роста цен нужно хотя бы стабилизировать цены. В противном случае фирме следует переориентироваться на другой вид деятельности.

<3 4 5 678 9 >

Дата добавления: 2016-06-15; просмотров: 2163;