Изокванта и ее анализ.

Производство с двумя переменными факторами.

Рассмотрим вариант, когда переменными являются два фактора производства, которые при определенном сочетании дают в результате один объем производимого продукта. Возьмем, например, затраты труда и капитала. Затраты труда обозначим за Х, затраты капитала - через Y. Изменение капитала и труда может происходить в обратном направлении. Если количество капитала (применяемого оборудования) увеличивается, то, следовательно, применение живого труда - уменьшается. При этом возрастание одного фактора и уменьшение другого происходят таким образом, что общий объем производства остается на прежнем уровне.

Эту зависимость можно представить графически с использованием изокванты (рис.5.2).

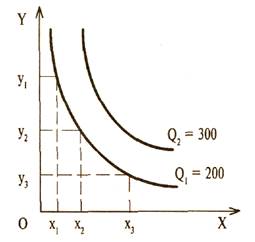
Рис. 5.2. Изокванта, отражающая производственную функцию с двумя переменными факторами.

Изокванта (или кривая равного продукта) – это кривая, точки которой отражают все возможные комбинации двух факторов, которые могут быть использованы для производства определенного объема продукта.

С увеличением объемов используемых переменных факторов, возникает возможность выпуска большого объема продукции. Изокванта, отражающая производство большего объема продукта, будет расположена правее и выше предыдущей изокванты.

Количество использованных факторов Х и Y может постоянно меняться, соответственно будет уменьшаться или увеличиваться максимальный выпуск продукта. Следовательно, может возникнуть множество изоквант, соответствующих разным объемам выпускаемой продукции, которые образуют карту изоквант (рис. 5.3).

Изокванты являются подобием кривых безразличия с той лишь разницей, что они отражают ситуацию не в сфере потребления, а в сфере производства. То есть изокванты обладают свойствами, близкими кривым безразличия.

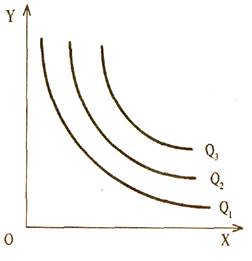
Рис. 5.3 Карта изоквант.

Отрицательный наклон изоквант объясняется тем, что увеличение использования одного фактора при определенном объеме выпуска продукта всегда будет сопровождаться уменьшением количества другого фактора.

Предельная норма технологического замещения (MRTS_xy) измеряется соотношением изменения фактора Y к изменению фактора Х, т.е. показывает сколько единиц фактора Y необходимо уменьшить, чтобы увеличить использование фактора на одну единицу. Поскольку замена факторов происходит в обратном отношении, то математическое выражение показателя MRTS_xy берется со знаком минус:

MRTS_xy = - _ΔY_

ΔХ

Можно отметить, что в верхней части изокванты угол будет достаточно велик, что говорит о том, что для изменения фактора Х на единицу требуются значительные изменения фактора Y. Следовательно, в этой части кривой значение MRTS_xy будет велико. По мере движения вниз по изокванте значение предельной нормы технологического замещения будет постепенно убывать. Это означает, что для увеличения фактора Х на единицу потребуется незначительное уменьшение фактора Y.

В реальных производственных процессах встречается два исключительных случая в конфигурации изоквант:

1) Ситуация, когда два переменных фактора соввершенно взаимозаменяемы, т.е. MRTS_xy = const (рис. 5.4). Подобную ситуацию можно представить при возможности полной автоматизации производства.

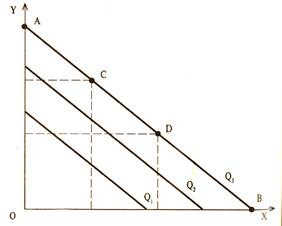
Рис. 5.4. Изокванта при совершенной взаимозаменяемости факторов, MRTS_xy = const .

2) Случай, когда они жестко взаимодополняют друг друга, т.е. MRTS_xy =0 (рис.5.5).

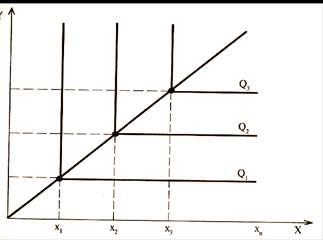
Рис. 5.5. Изокванта при жесткой дополняемости факторов, MRTS_xy =0