Истечение в атмосферу

Предположим, что есть резервуар, в боковой стенке которого выполнено малое отверстие (рис. 62). Уровень жидкости в резервуаре будем считать постоянным. Проведем плоскость сравнения через центр тяжести сжатого сечения и выберем два расчетных сечения: 1-1 по свободной поверхности жидкости и С-С в сжатом сечении.

Рисунок 62 - Схема истечения из отверстия.

Составим уравнение Бернулли для этих двух сечений.

,

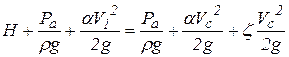где: Н - напор над центром тяжести отверстия,

Р_а - атмосферное давление,

V₁ - скорость на свободной поверхности жидкости,

V_c - в сжатом сечении струи,

α- коэффициент Кориолиса,

ξ- коэффициент местного сопротивления.

При истечении через отверстия или короткие насадки можно считать, что потеря напора состоит только из местных потерь, а потери на трение отсутствуют.

Обозначим через Н_о полный напор в сечении 1-1, тогда уравнение примет вид:

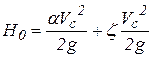, где .

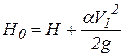Отсюда найдем выражение для средней скорости в сжатом сечении:

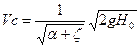или V_c=φ ,

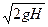так как Н ≈ Но (V₁≈0) и φ= 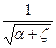- коэффициент скорости.

Коэффициент скорости представляет собой отношение действительной скорости истечения V_c к скорости истечения идеальной жидкости :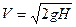

.

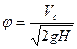Определим расход жидкости через отверстие из уравнения неразрывности:

Q = V_cω_с = ωεφ 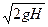, с учетом того, что ω_с= ωε ,

где ω_с- площадь сжатого сечения струи,

ω - площадь сечения отверстия,

ε - коэффициент сжатия струи (ε=ω_с/ω).

Коэффициент сжатия характеризует степень сжатия струи. Обозначим коэффициент расхода μ=εφ, тогда окончательную формулу расхода жидкости через отверстие можно представить в виде:

Q=μω .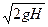

Коэффициент расхода характеризует отношение действительного расхода Q к расходу идеальной жидкости Q_ид=ω :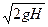

μ=Q/ω .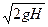

Для малых отверстий в тонкой стенке с совершенным сжатием коэффициент расхода μ≈0,6-0,62.

Однако, необходимо отметить, что коэффициенты расхода, сжатия и скорости зависят от режима истечения (числа Рейнольдса), результаты исследований А.Д.Альтшуля представлены на рисунке 63.

Рисунок 63 - Зависимость коэффициентов μ, φ, ε от числа Рейнольдса Re