Угол поворота вала двигателя за время пуска и торможения
В процессе работы механизма часто необходимо бывает знать положение РО в различные моменты времени в переходных режимах. Благодаря наличию жесткой механической связи между РО и валом двигателя, определив угол поворота вала двигателя, можно определить положение РО [1, 2, 4, 13] :
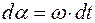 =>
=> 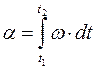 .
.
Следовательно, если вернуться к диаграмме изменения скорости, то якорь двигателя пройдет путь пропорциональный площади трапеции. В соответствии с уравнением движения 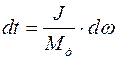 , =>
, => 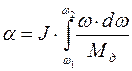 .
.
В частном случае, когда 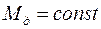 ,
, 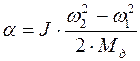 , то есть угол поворота вала двигателя пропорционален приращению кинетической энергии и обратно пропорционален динамическому моменту. Если двигатель разгоняется из неподвижного состояния до установившейся скорости, то
, то есть угол поворота вала двигателя пропорционален приращению кинетической энергии и обратно пропорционален динамическому моменту. Если двигатель разгоняется из неподвижного состояния до установившейся скорости, то 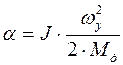 . Наименьший угол поворота вала двигателя будет при минимальном запасе кинетической энергии в системе.
. Наименьший угол поворота вала двигателя будет при минимальном запасе кинетической энергии в системе.
Очевидно, что при линейной зависимости динамического момента от скорости можно записать:
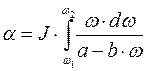 . (1.27)
. (1.27)
Вычислим этот интеграл. Для этого умножим числитель и знаменатель подынтегрального выражения на 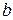 , а затем прибавим и вычтем
, а затем прибавим и вычтем 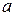 в числителе подынтегрального выражения:
в числителе подынтегрального выражения:
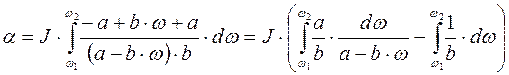
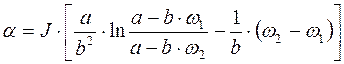
Подставив в это выражение 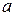 и
и 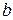 , получим:
, получим:
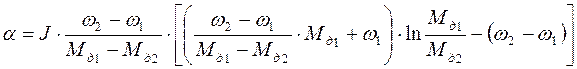 . (1.28)
. (1.28)
Полученное выражение позволяет найти перемещение РО за время переходного процесса. Используя его, легко построить зависимость 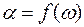 , а от нее легко перейти к зависимости
, а от нее легко перейти к зависимости 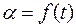 .
.
Дата добавления: 2016-06-15; просмотров: 2485;











