Общие сведения по курсу дисциплины ОТТС

1.3.1. Задачи курса. Дать знания по основам теории систем, методам выбора и системного обоснования структурных и функциональных параметров моделей систем, теории управления в формализованных системах. Научить методам синтеза и анализа моделей динамических управляемых систем. Дать навыки по обоснованию и применению алгоритмов управления, адаптации и самоорганизации, используемых в ТКС. Ознакомить с перспективными направлениями теории управления и адаптации, применительно к ТКС.

1.3.2. Тематика курса.

Основы теории систем. Основы системного подхода. Правила системной политики. Классификация систем, их свойства, функции, структура, характеристики.

Математические модели систем. Методы анализа и синтеза моделей. Адекватность моделей. Закономерности и свойства моделей. Автоматические и автоматизированные, концептуальные, формализованные кибернетические модели систем; оптимальное и ситуационное управление; критерии управления, роль лица принимающего решения (ЛПР); модели системы массового обслуживания, модели адаптивных и самоорганизующихся и интеллектуальных систем в телекоммуникациях.

Структурные модели систем. Представление структур. Основные параметры: сложность, связность, надежность структур. Оптимизация структур и кратчайших путей.

Функциональные модели (модели состояния) систем. Представление моделей через состояния и вероятности состояний. Уравнение состояния, наблюдаемость, управляемость, устойчивость. Аналоговая и дискретная модель. Обнаружение ситуаций. Формирующий фильтр. Анализ состояния систем, качество оценивания и управления. Хаотическая динамика, возникновение катастрофы.

1.3.3. Основной математический инструментарий в задачах системных исследований(подчеркнуты главенствующие составляющие).

1. Математика: детерминистская и вероятностная.

2. Представления вероятностных объектов: плотность (функция) распределения вероятностей, методы переменных состояния.

3. Состояния систем: статические, динамические.

4. Структурные и функциональные модели: вербальные, концептуальные, феноменологические, формализованные,«черного ящика», кибернетические,автоматные,дифференциальные,сетевые, графоаналитические.

5. Теоретико-множественное и аналитическое представление моделей: детерминистское, вероятностное, нечетное, логическое.

6. Анализ в частотной и временной областях.

7. Стохастические (вероятностные) модели:

- случайное событие (вероятность события А: );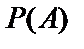

- случайная величина 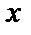(плотность распределения вероятностей );

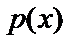- случайный процесс 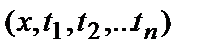(плотность распределения вероятностей 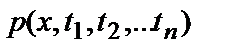); для марковского процесса задается переходная вероятность ;

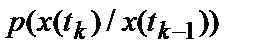- потоки случайных событий; марковские цепи; системы массового обслуживания;

- случайное поле ( 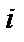-мерный процесс) 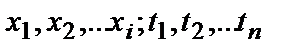(плотность распределения вероятностей );

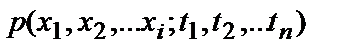- случайные временные ряды.

8. Свойства случайных процессов:

- стационарность – эргодичность, нестационарность, линейность, одномерность-многомерность,

- диффузионность (марковость, мартингальность).

9. Разложения функций в ряды: Фурье, Тейлора, Карунена-Лоева, Вольтерры, Котельникова, Уолша, Хаара, Радемахера, временные ряды, вейвлеты.

10. Оценки и характеризация случайных событий, величин и процессов.

- методы математической статистики, выборочные оценки, роль независимой выборки, интервал корреляции и дискретизации, эффективность, несмещенность состоятельность, достаточность.

- модели случайных процессов, марковость, рекурсивные оценки, алгоритмы стохастической аппроксимации, фильтры Калмана-Бьюси.

- критерии и качество оценок, достижимость параметров систем.

11. Управления в динамических системах.

- Методы ситуационного и оптимального управления;

- Принципы управлений по отклонению и по возмущению;

- Роль ограничений;

- Теорема о разделении и теорема двойственности;

- Инвариантность;

- Устойчивость.