Математическая модель задачи

1. Уравнение цели

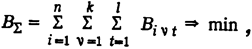
где В_S - суммарный расход условного топлива на отпуск электрической и тепловой энергии по энергосистеме за планируемый период; В_{i n t}, у t - суммарный расход условного топлива на отпуск электрической и тепловой энергии i-й электростанции на n-м виде топлива на t-й расчетный интервал времени (квартал, год); i = 1,2, ..., n - номер эквивалентной тепловой станции; n = 1, 2, ... , k-номер используемого эквивалентного вида топлива; l = 1,2, ..., l - номер расчетного интервала времени. В развернутом виде уравнение цели имеет следующий вид:

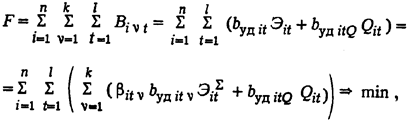
где b_itn - доля выработки электроэнергии на n-м виде топлива в суммарной выработке i-го объекта в t-м расчетном интервале; Q_it - отпуск тепла i-го объекта в t-м интервале; Э_it^S- суммарная выработка электроэнергии i-го объекта на всех сжигаемых видах топлива; b_{уд itQ} и b_{уд itn} - удельные расходы топлива на отпуск тепла и электроэнергии для i-го объекта в t-м интервале времени.

В качестве независимых переменных применяются значения мощностей эквивалентных электростанций. Изменяя мощности, можно изменять режим электростанций в заданном графике нагрузки системы, а изменяя поступление топлива, можно определять оптимальный вариант распределения топливных ресурсов системы.

2. Уравнения связи - эквивалентные характеристики узлов, которые дают связь между мощностью узла и требуемым видом топлива. Расход топлива оценивается в условных единицах. 3. Уравнение ограничений. В задаче учитывается множество ограничений (здесь даются только их перечень и некоторые пояснения):

а) по отпуску электроэнергии и максимальным мощностям электростанций; б) по балансу энергии в ЕЭС; в) по балансу мощностей в ЕЭС; г) по межсистемным перетокам мощности; д) по выполнению планов отпуска электроэнергии и тепла; е) по возможности снабжения электростанций топливом от заданных месторождений; задается матрица возможных месторождений для поставок топлива электростанциям, сжигающим n-й вид топлива;

ж) по поставкам контролируемого вида топлива; для учета топливной конъюнктуры, т. е. дефицитных видов топлива, вводятся ограничения по его использованию на данном интервале времени;

з) по емкости топливных складов - запас топлива не должен быть меньше страхового значения и больше максимальной емкости склада;

и) по запасам топлива на конец планируемого периода; к) по поставкам топлива из определенного месторождения; поставки не должны превышать предельную производительность месторождения;

л) по разгрузочным возможностям топливно-транспортных цехов электростанций;

м) по балансу топлива на планируемый год; балансируются выделенные ресурсы и потребность в топливе.

4. Уравнение оптимизации. Для оптимизации используется метод градиентов.

Программа расчетов предусматривает возможность решения задачи для систем, имеющих 150 эквивалентных объектов, 30 электрических узлов, 20 контролируемых ЛЭП, 25 эквивалентных видов топлива. Число расчетных интервалов равно 12. Общее число независимых переменных в каждом расчетном интервале времени может быть равно 600, а суммарное число источников получения топлива не должно превышать 120.

Оптимальный баланс по натуральному топливу. Топливно-энергетический баланс по натуральному топливу может составляться с использованием метода линейного программирования (см. рисунок ниже). Для i объектов (тепловых станций, групп оборудования, эквивалентных узлов) задаются марки и виды топлива, возможные к использованию, технологические пределы по использованию видов натурального топлива, потребность в условном топливе. Для подразделений энергетики от станций до единой системы могут задаваться и конъюнктурные ограничения. Тогда целевая функция имеет вид

Ц = ,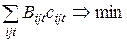

где 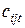- коэффициенты, учитывающие эффективность использования топлива определенного вида j. они отражают цены на топливо, КПД его использования на станциях, конъюнктуру и др.

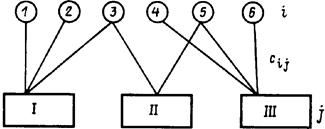
Схема для расчета топливно-энергетического баланса

Учитываются также ограничения:

суммарный объем выделенных энергоресурсов должен обеспечить плановое производство электроэнергии;

на определенные объекты должно поступать топливо определенного вида и количества;

поставки топлива должны быть положительные (не отрицательные), что требуется методом линейного программирования.

Эта задача имеет чрезвычайно высокую размерность и может быть решена только с применением эквивалентирования и декомпозиции. Для районной энергосистемы число переменных составляет 100-200. Для снижения размерности блочное оборудование ТЭС группируется по номинальному давлению пара турбоагрегатов, применяются эквивалентные марки топлива, сжигание которых примерно равнозначно для данного оборудования, применяются эквивалентные энергетические характеристики объектов.

Ввиду применения эквивалентирования и ограничений топливно-энергетический баланс может "не получиться", это требует повторных расчетов в целях взаимоувязки всех условий задачи. Современные программы расчетов предусматривают диалоговый режим, что позволяет разработчику выполнять вариантные расчеты и получать оптимальный и обоснованный план.

Вопрос для самостоятельного изучения: Оптимизация режимов водохрани­лищ гидростанций.