режима энергосистемы

Мощности электрических станций и параметры режима сети могут определяться при поэтапном решении комплексной задачи. На первом этапе определяются активные мощности станций и приближенно рассчитывается режим электрической сети, в которой считаются известными реактивные мощности в ветвях, напряжения в узлах, коэффициенты трансформации трансформаторов. На втором этапе считаются известными активные мощности станций и рассчитываются все параметры электрической сети.

Если не учитывать ограничения в форме неравенств по пропускным способностям ВЛ и мощностям электростанций, то задача комплексной оптимизации может решаться методом множителей Лагранжа, причем полученные оптимизационные уравнения позволяют решать задачу поэтапно.

Пусть в энергосистеме на параллельную работу включено п активных и т реактивных источников мощности, связанных с узлами нагрузки сетью произвольной конфигурации. Целевая функция такой оптимизационной задачи имеет вид

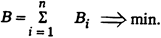
Ограничение по балансу активной мощности имеет вид

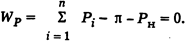
Аналогично по реактивной мощности

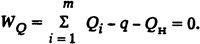
Здесь p и q- потери активной и реактивной мощностей в электрических сетях.

Функция Лагранжа включает эти два уравнения ограничений и имеет вид

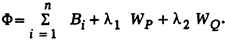
Решение находится из уравнений

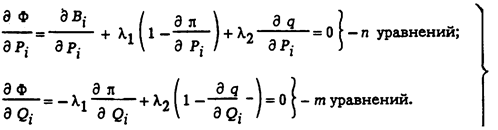
Найдем из уравнений второй группы отношение l₂ и l₁:

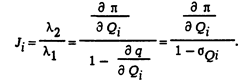
Обозначим 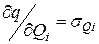дифференциальный показатель (относительный прирост) потерь реактивной мощности в сети. Он показывает, насколько возрастают потери реактивной мощности во всей электрической сети при изменении реактивной нагрузки 1-го источника на дQ_i.

Записав это уравнение для каждого из т источников реактивной мощности и приравняв правые части, получим условие наивыгоднейшего распределения реактивных мощностей энергосистемы

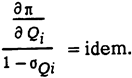
Обратимся теперь к уравнениям первой группы в. Запишем одно из них в виде

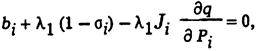
где s_i — дифференциальный показатель (относительный прирост) потерь активной мощности в системе.

Подставим в последние уравнение значение J_i и получаем

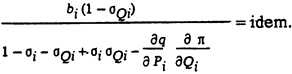
Это общее условие наивыгоднейшего распределения активной и реактивной нагрузок в сложной энергосистеме с учетом потерь мощности в электрической сети.

Если активная и реактивная мощности распределяются независимо, то это уравнение распадается на два:

(*)

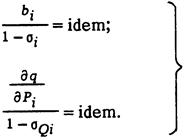Можно показать, что общее условие наивыгоднейшего распределения нагрузки для однородной электрической сети, т.е. для сети, у которой для всех элементов отношение удельных активного и реактивного сопротивлений r₀/x₀ = const, упрощается. Для таких сетей выполняется условие

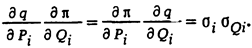
Условие наивыгоднейшего распределения нагрузки в однородных сетях имеет вид

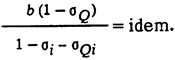
Используя (*), можно поэтапно оптимизировать режим энергосистемы. Кроме упомянутых ограничений, могут быть и другие: по напряжениям, углу сдвига фазы в передачах и пр. Тогда растет число множителей Лагранжа, и процесс оптимизации усложняется. Кроме того, при расчете режима сети рассчитывается и запоминается матрица коэффициентов токораспределения. При высокой размерности задачи и необходимости учета разнообразных ограничений процесс расчета плохо сходится. Все это является недостатком рассмотренного алгоритма, поэтому он применяется для концентрированных энергосистем или в совокупности с другими методами оптимизации режима.

РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ АГРЕГАТАМИ ЭЛЕКТРОСТАНЦИЙ

Использовав метод неопределенных множителей Лагранжа, можно получить условие наивыгоднейшего распределения нагрузки между агрегатами электростанции в виде равенства отношения приращения первичного ресурса (подведенной мощности) к приращению вторичного (полезной мощности) при соблюдении балансовых соотношений.

Распределение нагрузки между агрегатами тепловых станций. Для ТЭС возникают задачи распределения нагрузки между турбинами, котлами, блоками, частями станции. Простые условия наивыгоднейшего распределения получаются лишь для конденсационных турбоагрегатов, блоков и котлов. Условия наивыгоднейшего распределения нагрузки: между конденсационными турбинами

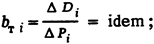
между котлами

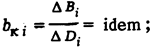
между блоками

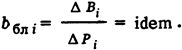
Легко показать, что

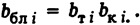
Условия наивыгоднейшего распределения нагрузки между частями станции аналогичны, но каждая часть представляется эквивалентной характеристикой (эквивалентными характеристиками турбин, котлов, частей станции).

Условные обозначения: 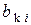, - относительный прирост котла, который показывает изменение расхода условного топлива котла 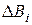при изменении паросъема на 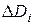; 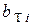, - относительный прирост турбины, который показывает изменение расхода пара 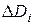при изменении мощности турбин на 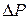; 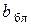– относительный прирост блока.

В практических условиях на приведенные 3 условия могут накладываться ограничения, определяемые видом агрегатных характеристик. Характеристики могут иметь скачки, участки с постоянными относительными приростами и т. п.

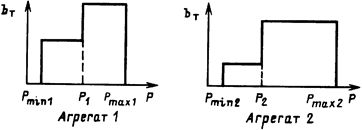
К распределению нагрузки при ступенчатых характеристиках агрегатов

Если нагрузка распределяется между турбинами, которые имеют ступенчато-кусочные характеристики ( см. рисунок), то агрегаты загружаются в порядке возрастания их относительных приростов. Например, при росте нагрузки от минимальной Р_min = P_min1 + P_min2 вначале загружается агрегат 2, поскольку он имеет наименьший относительный прирост. Если нагрузка превышает P_min1+ Р₂ то загружается агрегат 1, затем при нагрузке, большей Р₁+Р₂ снова загружается агрегат 2, а при Р1+Р_max2 агрегат 1, при этом сохраняется принцип использования тех агрегатов, которые дают большую экономию топлива. Это же положение распространяется и на методику распределения нагрузки между блоками и котлами. Таким образом, если агрегаты не имеют равных относительных приростов, то они загружаются в порядке возрастания относительных приростов.

Более сложными являются условия распределения нагрузки для станций, имеющих теплофикационные турбины. Для них относительные приросты зависят не только от электрической мощности, то также и от расхода пара, идущего в производственные отборы, D_п. При распределении нагрузки между турбинами с отборами условия наивыгоднейшего распределения нагрузки имеют вид:

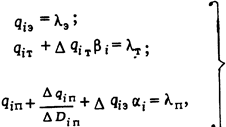
где 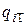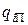- относительные приросты расхода теплоты при изменении величины отбора (теплофикационного и производственного) и постоянстве электрической мощности; 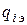- относительный прирост расхода теплоты при изменении электрической мощности; 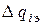, , 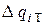, 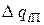b_i , a_i - величины, которые могут быть найдены при аналитической записи диаграммы режимов турбины.

Имеется множество частных случаев тепловых схем ТЭС и состава их оборудования. Для них можно получить условия наивыгоднейшего распределения нагрузки, которые нашли широкое практическое применение.

Распределение нагрузки между агрегатами гидростанцийДля гидростанций наивыгоднейшее распределение нагрузки будет в том случае, когда агрегаты работают с равными относительными приростами:

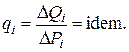
Из полученных условий следует, что методика решения задачи о наивыгоднейшем распределении нагрузки между агрегатами электростанций проста, если известны их характеристики относительных приростов и они удовлетворяют требованиям метода Лагранжа.

Вопрос для самостоятельного изучения: В чем отличие оптимального распределения нагрузки между агрегатами ТЭС и ГЭС?