ИССЛЕДОВАНИЕ ОПЕРАЦИОННОГО УСИЛИТЕЛЯ
Операционным усилителем называют дифференциальный усилитель постоянного тока, предназначенный для выполнения различных операций над аналоговыми величинами при работе в схемах с отрицательной обратной связью.
Операционный усилитель, как правило, имеет один выход и два входа: прямой и инверсный. Инверсный вход обозначают знаком инверсии (кружком) или помечают знаком «-». Прямой вход не имеет знака инверсии или его помечают знаком «+». Выходное напряжение находится в фазе с напряжением на прямом входе и противофазно напряжению на инверсном входе. Операционный усилитель, как правило, обладает большим коэффициентом усиления по напряжению (Кu>2000). Применяют операционные усилители в схемах с отрицательными обратными связями. При этом характер операций, выполняемых над входными сигналами, определяется параметрами элементов, включенных во входной цепи и в цепи обратной связи.
Если во входной цепи и в цепи обратной связи включены активные сопротивления (рис. 6.1, а), то получим масштабный операционный усилитель. При этом
Uвых = - (R0/R1)Uвх . (6.1)
Если на вход усилителя подать несколько сигналов (рис. 6.1, б), то напряжение на выходе определится алгебраической суммой входных сигналов с соответствующими масштабными коэффициентами.
UВЫХ = -(UВХ1 R0/R1 + UВХ2 R0/R2 + UВХ3 R0/R3). (6.2)
При включении во входной цепи активного сопротивления, а в цепи обратной связи - конденсатора (рис. 6.1, в), получим интегрирующий операционный усилитель:
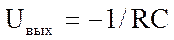
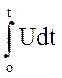 (6.3)
(6.3)
Если во входной цепи включен конденсатор, а в цепи обратной связи - активное сопротивление (рис. 6.1, г) получим дифференцирующий операционный усилитель:
Uвых=- RdUвх/dt (6.4)
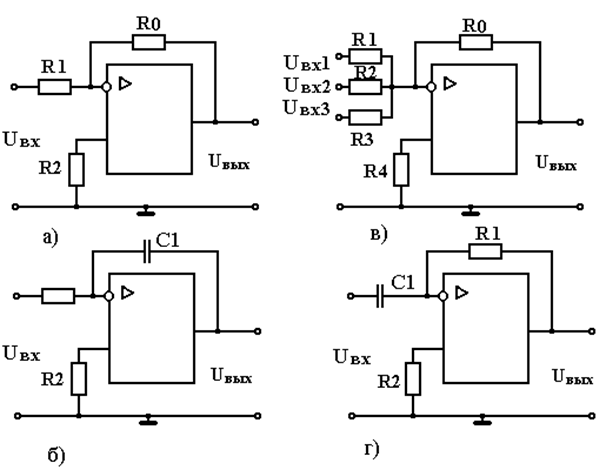
Рисунок 6.1 - Схемы масштабного (а), суммирующего, (б)
интегрирующего (в) и дифференцирующего (г)
операционного усилителя
6.2 Порядок выполнения работы
6.2.1Собрать схему масштабного операционного усилителя (рис. 6.2,а).
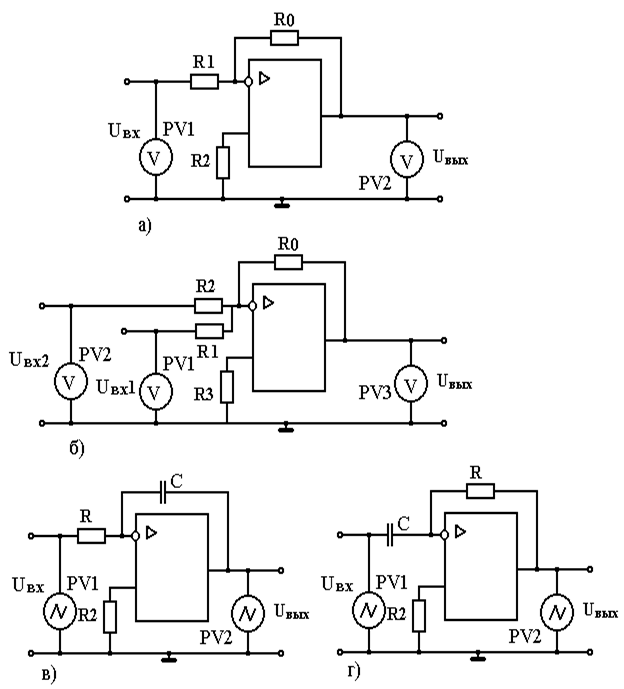
Рисунок 6.2 - Схемы исследования масштабного (а), суммирующего (б),
интегрирующего (в) и дифференцирующего (г)
операционного усилителя
6.2.2 Устанавливая различные значения сопротивлений на входе и в цепи обратной связи, а также, подавая на вход различные напряжения, определить UВЫХ. Расчетные значения UВЫХ определить по формуле (6.1). Результаты измерений и вычислений занести в табл. 6.1.
Таблица 6.1
| R1, Ом | R0, Ом | U1, В | UВХ, В | UВЫХ, В |
| экспер. | расчет. | |||
6.2.3.Собрать схему суммирующего операционного усилителя (рис.6.2, б).
Устанавливая заданные значения входных напряжений и сопротивлений, определить UВЫХ. Расчетные значения UВЫХх определить по формуле (6.2). Результаты вычислений и измерений занести в табл. 6.2.
Таблица 6.2
| R1, Ом | R2, Ом | R0, Ом | U1, В | U2, В | UВЫХ, В | |
| экспер. | расчет. | |||||
6.2.4. Собрать схему интегрирующего операционного усилителя (рис. 6.2, в).
6.2.5. Устанавливая заданные значения R и C и подавая на вход заданные сигналы, проанализировать выходные сигналы. Результаты исследований представить в виде графиков UВЫХ = ¦(t), UВХ = ¦(t). Расчетную функцию UВЫХ.РАСЧ = ¦(t) определить по формуле 6.3.
6.2.6. Повторить исследования, указанные в пункте (6.2.5), для дифференцирующего операционного усилителя. Расчетную функцию UВЫХ.РАСЧ = ¦(t) определить по формуле 6.4.
ИССЛЕДОВАНИЕ ЭЛЕМЕНТОВ ЦИФРОВОЙ ЛОГИКИ
Логические элементы составляют основу устройств цифровой (дискретной) обработки информации и цифровых устройств автоматики.
Логические элементы выполняют простейшие логические операции над цифровой информацией. Логическая операция преобразует по определенным правилам входную информацию в выходную. Логические элементы чаще всего строят на базе электронных устройств, работающих в ключевом режиме. Поэтому цифровую информацию обычно представляют в двоичной форме, в которой сигналы принимают только два значения: «0» (логический нуль) и «1» (логическая единица) соответствующие двум состояниям ключа.
Основными логическими элементами являются элементы ИЛИ, И, НЕ, ИЛИ-НЕ, И-НЕ.
Логический элемент ИЛИ (рис. 7.1, а) реализует функцию логического сложения или дизъюнкции. Обозначается в случае двух независимых переменных У = Х1ÚХ2 либо У = Х1 + Х2 (читается Х1 или Х2) и определяется таблицей истинности (табл. 7.1). Операцию ИЛИ можно выполнять для трех и более независимых аргументов. Функция У = 1, если хотя бы одна из независимых переменных Хi равна единице.
Логический элемент И (рис. 7.1, б) реализует функцию логического умножения или конъюнкции. Обозначается У = Х1ÙХ2 либо У = Х1Х2 (читается Х1 и Х2) и определяется таблицей истинности (табл. 7.2). Операцию логического умножения можно распространить на три и более независимых аргументов. Функция У равна единице только тогда, когда все независимые переменные Хi равны единице.
Логический элемент НЕ реализует операцию логического отрицания или инверсии. Логическое отрицание от функции Х обозначается `Х (говорится «не Х») и определяется таблицей истинности (табл. 7.3)
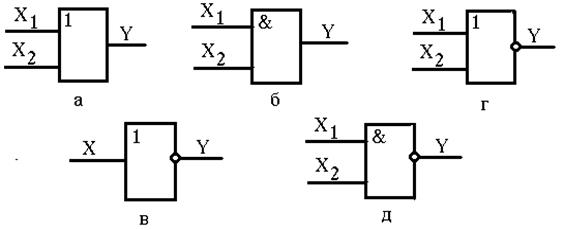
Рисунок 7.1 – Условно-графические изображения логических элементов ИЛИ (а), И (б), НЕ(в), ИЛИ-НЕ(г), И-НЕ(д)
Таблица 7.1 – Таблица истинности Таблица 7.2 – Таблица истинности элемента ИЛИ элемента И
| Х1 | Х2 | У = Х1 +Х2 | Х1 | Х2 | У = Х1Х2 | ||
Таблица 7.3 – Таблица истинности Таблица 7.4 – Таблица истинности
элемента НЕ элемента ИЛИ + НЕ
| Х | ` 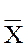
| Х1 | Х2 | У = ` 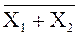
| ||
Таблица 7.5- Таблица истинности элемента И-НЕ
| Х1 | Х2 | У= 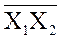
|
Логический элемент ИЛИ-НЕ реализует логическую функцию
У = 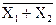 и определяется таблицей истинности (табл. 7.4).
и определяется таблицей истинности (табл. 7.4).
Логический элемент И-НЕ реализует логическую функцию У = 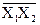 и определяется таблицей истинности (табл. 7.5).
и определяется таблицей истинности (табл. 7.5).
Для рассмотренных логических элементов сигнал на выходе определяется входными сигналами в данный момент времени и не зависит от предыдущих значений входных и выходных сигналов. Логические устройства построенных на основе таких элементов называются комбинационными.
Комбинационные устройства, в которых имеется однозначная связь между входными и выходными сигналами не исчерпывают возможности логических устройств. Часто бывает необходимо запомнить факт поступления входного сигнала после того как этот сигнал будет снят или задать последовательность работы устройства, то есть очередность выполнения операций. Такая задача возникает, в частности, при счете импульсов, когда устройство должно не только реагировать на поступление входного сигнала, но и учитывать предыдущее состояние. Такого рода последовательные логические устройства создаются на основе использования триггеров.
Триггером называется устройство, имеющее два устойчивых состояния. При отсутствии внешних воздействий триггер может сколь угодно долго находиться в одном из устойчивых состояний. Входной сигнал может перевести триггер из одного устойчивого состояния в другое.
Триггер обычно имеет два выхода, обозначенные Q и`Q. Единичным считается состояние триггера, при котором Q = 1, а `Q = 0, а нулевым – Q = 0, `Q = 1.
Простейшим триггером является асинхронный RS-триггер (рис. 7.2). Его работа определяется таблицей истинности (табл. 7.6).
При входных сигналах S = 1, R = 0 триггер устанавливается в единичное состояние (Q = 1, `Q = 0), а при входных сигналах S = 0, R = 1 – в нулевое состояние (Q = 0, `Q = 1). При S = 0, R = 0 триггер не меняет своего состояния. Таким образом, триггер является элементом памяти, так как сохраняет информацию о последней из поступивших команд при отсутствии новых команд на входах. Сочетание входных сигналов S = 1, R = 1 является недопустимым, так как при этом в RS-триггере возникает неопределенность.
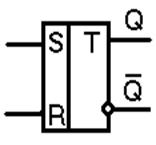
Таблица 7.6 – Таблица истинности
синхронного RS-триггера
| S | R | Q n+1 | ||
| Q n | ||||
| ||||
| неопределенность |
RS-триггер может быть построен на различных логических элементах.
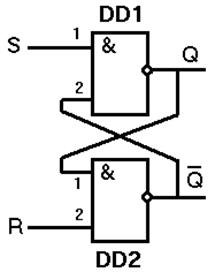
На рис. 7.3, а показана реализация RS-триггера на логических элементах ИЛИ-НЕ. В схеме имеются обратные связи (ОС) с выходов триггера на входы логических элементов. Именно наличие ОС отличает триггеры от ранее рассмотренных комбинационных устройств: сигнал ОС позволяет в триггере учитывать его предыдущее состояние.
Проверим соответствие работы схемы рис. 7.3, а и табл. 7.6.
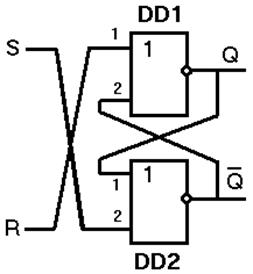
а б
Рисунок 7.3 – Реализация RS-триггера с прямыми входами на элементах ИЛИ-НЕ (а) и RS-триггера с инверсными входами на элементах И-НЕ (б)
Пусть S = 1, R = 0, тогда независимо от сигнала на входе 1 элемента ДД2 на его выходе получим 0, т.е.`Q = 0. На обоих входах ДД1 Получим нулевой сигнал и, значит, Q = 1. По цепи обратной связи сигнал логической единицы будет подан на вход 1 элемента ДД1, что и обеспечит сохранение единичного состояния триггера (Q = 1, `Q = 0) после снятия входного сигнала, т.е. при S = 0, R = 0. При поступлении на вход комбинации сигналов S = 0, R = 1 на выходе ДД1 однозначно получим 0, т.е. Q = 0 и значит `Q = 1. Подача этого сигнала по цепи обратной связи на вход 2 элемента ДД1 обеспечит запоминание данного состояния, т.е. сохранение триггером нулевого состояния (Q = 0, `Q = 1) при снятии входного сигнала (при S = 0, R = 0).
Если на вход подадим комбинацию S = 1, R = 1, получим Q = 1, `Q = 1. Эта комбинация является неприемлемой по двум причинам:
1 не выполняется условие взаимной инверсности выходов триггеров (т.е. условие, что если Q = 1, то `Q = 0 и наоборот);
2 состояние Q = 1, `Q = 1 является неустойчивым. После снятия входных сигналов S ® 0, R ® 0 триггер не сохранит свое состояние, а равновероятно перейдет в состояние Q = 1, `Q = 0 либо Q = 0, `Q = 1.
Триггер, построенный по схеме, приведенной на рис. 7.3, а и изображаемый при интегральном исполнении как показано на рис. 7.2 является триггером с прямыми входами. Он переключается единичным сигналом или фронтом импульса. Триггер, построенный по схеме, приведенной на рис. 7.3, б, переключается нулевым сигналом или срезом импульса и называется RS-триггером с инверсными входами. При S = 0, R = 1 на выходе ДД1 однозначно получаем 1, т.е. Q = 1. При этом на обоих входах ДД2 имеем сигнал 1, а значит`Q = 0. На вход 2 элемента ДД1 по цепи обратной связи будет подан нулевой сигнал, что и обеспечит сохранение триггером единичного состояния (Q = 1, `Q = 0) при входном сигнале S = 1, R = 1. Аналогично можно показать, что при входном сигнале S = 1, R = 0 триггера переключится в нулевое состояние (Q = 0, `Q = 1) и сохранит его при S = 1, R = 1. Запрещенной для RS-триггера с инверсными входами является комбинация S = 0, R = 0.
Изображение на схемах асинхронного RS-триггера с инверсными входами приведено на рис. 7.4, а его работа определяется таблицей истинности (табл. 7.7).
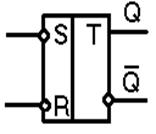 Таблица 7.7 – Таблица истинности асинхрон-
Таблица 7.7 – Таблица истинности асинхрон-
ного RS-триггера с инверсными входами
| S | R | Q n+1 |
| Q n | ||
| Неопределенность |
Рисунок 7.4 - Асинхронный
Дата добавления: 2016-06-09; просмотров: 1956;











