Вычислимость минимизации

Теорема 12.6. Пусть функция 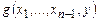вычислима на МПД. Тогда вычислима и функция

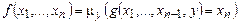Доказательство. Пусть G — программа стандартного вида, вычисляющая функцию g. Пусть 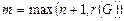. Построим программу F для вычисления функции f по следующему алгоритму: вычислять 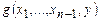при y = 0, 1, 2, … до тех пор, пока не найдется y, такой, что 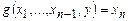, тогда y будет требуемым выходом. Помещаем 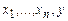в регистры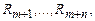 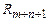. Полагаем в начале y = 0. Промежуточное значение 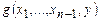помещаем в 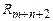. Программа для вычисления f:

…

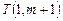
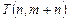
I_p: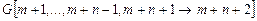

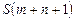
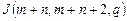
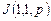
I_q: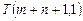

Следовательно, функция f вычислима, что и требовалось доказать.

Следствие 12.6. Частично рекурсивные функции вычислимы на МПД, т.е. Ч Í Е.

Покажем теперь частичную рекурсивность вычислимых функций.

Теорема 12.7. Всякая вычислимая на МПД функция является частично рекурсивной.

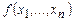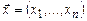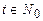Доказательство. Пусть — вычислимая на МПД функция и пусть P = I₁I₂…I_s — соответствующая программа. Будем называть шагом вычисления выполнение одной команды программы. Для произвольных и определим следующие функции, связанные с вычислением :

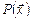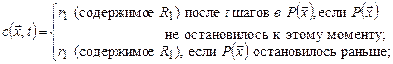
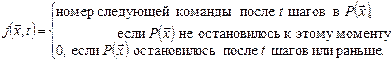
Таким образом, 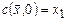, 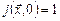. Очевидно, что функции 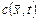, 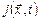всюду определены. Найдем теперь выражение для 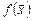через введенные функции. Если значение 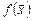определено, то 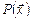останавливается после t₀ шагов, где 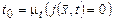, поэтому 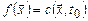. Если же значение 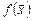не определено, то 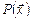не останавливается, и тогда 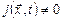для любых 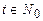, поэтому 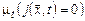не определено. Следовательно, во всех случаях .

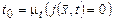Теперь, если убедиться, что функци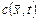и и 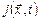частично рекурсивны, то таковой будет и функция 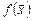. Ясно, что существует неформальный алгоритм вычисления значений функци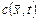й и 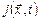. Для этого нужно по заданным 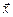, t написать последовательность конфигураций K₀ à K₁ à … à K_t и выписать содержимое регистра R₁ и номер выполняемой на шаге t + 1 команды. По тезису Черча функции 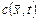и 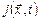частично рекурсивны и, значит, функция 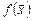является частично рекурсивной, что и требовалось доказать.

Замечание 12.8. Более точный анализ показывает, что функци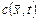и и 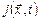являются примитивно-рекурсивными.

Следствие 12.9. Классы функций Ч и Е совпадают.

Рассмотрим теперь вопрос о соотношении введенных классов Ч_пр, Ч₀ и Ч.

Поскольку класс Ч содержит частично определенные функции, то ясно, что Ч₀ Í Ч. Кроме того, очевидно, что Ч_пр Í Ч₀. Вопрос о том, является ли включение Ч_пр Í Ч₀ собственным решается несколько сложнее.

Первый пример общерекурсивной функции, не являющейся примитивно рекурсивной, был дан Аккерманом (1928).

Функция Аккермана 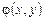задается соотношениями:

;

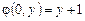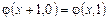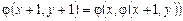Можно доказать, что данные соотношения однозначно определяют функцию 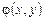. Результаты вычислений убеждают, что имеется алгоритм вычисления функции .

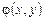В то же время доказывается, что функция 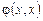не является примитивно рекурсивной, так как растет быстрее, чем любая одноместная примитивно рекурсивная функция. Доказательство, ввиду его громоздкости, опускается[6].