Нумерация наборов чисел и слов

В теории алгоритмов получил распространение прием, позволяющий сводить изучение функций от нескольких переменных к изучению функций одной переменной. Он основан на нумерации наборов чисел так, что имеется биективное соответствие между наборами чисел и их номерами, причем функции, определяющие по набору чисел его номер и по номеру сам набор чисел являются общерекурсивными.

Рассмотрим сначала множество — множество пар натуральных чисел. Рассмотрим следующее упорядочение этих пар, называемой канторовским:

(0, 0), (0, 1), (1, 0), (0, 2), (1, 1), (2, 0), … (13.1)

Здесь в порядке возрастания 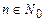упорядочиваются пары (x, y) с условием x + y = n в виде последовательности

(0, n), (1, n – 1), …, (x, y), …, (n, 0). (13.2)

Пусть c(x, y) — номер пары (x, y) в последовательности (13.1), причем считаем c(0, 0) = 0. Если c(x, y) = n, то обозначим через r, l — функции, удовлетворяющие x = l(n), y = r(n) и, следовательно, c(l(n), r(n)) = n.

Покажем, что функции c, l, r в явном виде выражаются через обычные арифметические функции. Произвольная пара (x, y) находится на месте x + 1 в последовательности (13.2). Далее, перед последовательностью (13.2) находятся последовательности, отвечающие элементам (x, y) с условием x₁ + y₁ = t, где t = 0, 1, …, x + y – 1, и каждая из них содержит t + 1 элемент.

Следовательно, элемент (x, y) находится в последовательности (13.1) на месте 1 + 2 + … + x + y + x + 1. Поскольку нумерация начинается с нуля, то номер элемента (x, y) в последовательности (13.1) равен

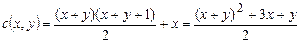. (13.3)

Пусть теперь c(x, y) = n и найдем x = l(n) и y = r(n). Из (13.3) следуют равенства:

;

;

.

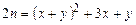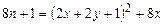Следовательно, или

.

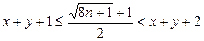Это означает, что

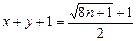. (13.4)

Теперь, используя (13.3), определяем x:

.

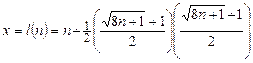Подставляя найденное значение x в (13.4), получаем y:

.

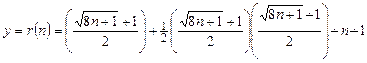Заметим, что важен не сам вид полученных функций c(x, y), r(n), l(n), а важен факт их эффективной вычислимости.

Теперь с помощью нумерации пар чисел легко получить нумерацию троек чисел, т.е. элементов множества 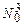. Определим функцию 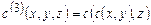. Тогда, если 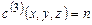, то z = r(n), y = r(l(n)), x = l(l(n)).

Аналогично, для наборов произвольной длины r + 1 полагаем

, , …,

…

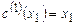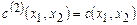и по определению называем число канторовским номером n-ки 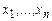. Если , то x_n = r(m), x_{n – 1} = r(l(m)), …, x₂ = r(l(…l(m)), x₁ = l(l(…l(m)).

Теперь, имея нумерацию множеств (k > 0), можно установить нумерацию множества 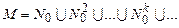. Положим для любого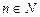 . Ясно, что с — биективное соответствие между М и N₀. Кроме того, если , то , . Отсюда эффективно определяются .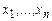

Приведем еще одну нумерацию наборов чисел. Номер пары (x, y) зададим функцией

.

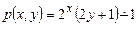Ясно, что это общерекурсивная функция. При этом, если p(x, y) = n, то выполнено 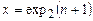, 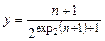. Следовательно, для данной нумерации , .

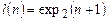Теперь, имея нумерационную функцию для пар чисел, аналогично предыдущему строим нумерационные функции для к-ок чисел и множества наборов .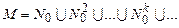

Другую нумерацию множества М можно получить так. Пусть

.

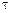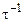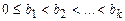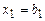Ясно, что — вычислима. Чтобы установить вычислимость , заметим, что каждое натуральное число имеет единственное представление в двоичной позиционной записи. Т.е. для любого n можно эффективно и однозначно найти k > 0 и такое, что . Откуда получаем , где , (0 < i < k).

Рассмотрим теперь вопрос о нумерации слов в некотором алфавите и укажем некоторые из применяемых способов такой нумерации.

Пусть 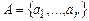— конечный алфавит и пусть 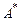— множество всех слов конечной длины в алфавите А, включая и пустое слово ^.

Алфавитная нумерация определяется следующим образом:

c(^) = 0, .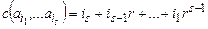

Поскольку при фиксированном r каждое положительное число n однозначно представимо в виде

, (0 < i_j < r + 1),

то каждое число есть алфавитный номер одного и только одного слова из множества 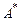. Разложение (16) называется r-ичным разложением числа n с цифрами 1, …, r в отличии от обычного r-ичного разложения с коэффициентами 0, …, r – 1.

Нумерация слов через нумерационные функции. Пусть имеется счетный алфавит 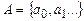. Тогда нумерация слов определяется так:

v(^) = 0, ,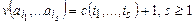

где функция определена выше. Ясно, что так определенная функция v является биективной и вычислимой.

Геделевская нумерация. Пусть имеем счетный алфавит 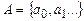. Определим геделевы номера для каждой буквы 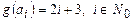. Теперь для каждого слова 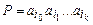определим геделев номер 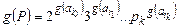, где — k-е простое число. Кроме того, положим g(^) = 1. При этом геделев номер последовательности слов P₀, P₁, …, P_k определяется так: .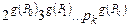

Рассмотрим теперь два применения нумерационных функций.

Утверждение 13.1. а) Функция f(x, y), отличная от нуля на конечном множестве пар из 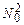, общерекурсивна.

Доказательство. Действительно, пусть 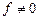на парах чисел 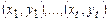и пусть имеет на них значения z₁, …, z_t. На остальных пара f(x, y) = 0. Положим , где c — нумерационная функция Кантора.

Определим функцию g так: 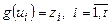, g(u) = 0 на остальных . Было выше показано, что g — общерекурсивна. По построению выполнено f(x, y) = g(c(x, y)) и поэтому f — общерекурсивна.

б) Определим сначала понятие совместной рекурсии. В схеме совместной рекурсии функция порождается с помощью нескольких функций.

Пусть для определенности даны функции 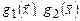, , здесь 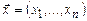. Тогда можно определить пару функций и по рекурсии:

,

,

,

.

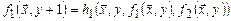Утверждение 13.2. Если g₁, g₂, h₁, h₂ — общерекурсивные функции, то f₁, f₂ также общерекурсивны.

Доказательство. Определим функцию

,

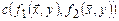где c — нумерационная функция Кантора. Тогда имеем: 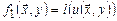, . Далее имеем

—

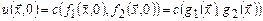частично рекурсивная по условию.

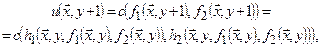
т.е. функция получается по схеме обычной рекурсии с помощью функций

,

.

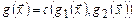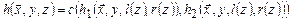Значит функция — частично рекурсивная, а потому частично рекурсивны и функции и , что и требовалось доказать.

Л е к ц и я 14