Нумерация машин Тьюринга
Зафиксируем счетные множества символов {a0, a1, …, ai, …} и {q0, q1, …, qj, …} и будем считать, что внешние алфавиты и алфавиты внутренних состояний всех машин Тьюринга берутся из этих множеств. При этом будем считать, что a0 принадлежит всем внешним алфавитам машин и интерпретируется как пустой символ, а буквы q0, q1 принадлежат всем внутренним алфавитам машин и всегда означают заключительное и начальное состояния соответственно. Опишем теперь единый способ представления информации о машинах с помощью кодирования. Каждому символу из множества {L, R, E, a0, a1, …, ai, …, q0, q1, …, qj, …} поставим в соответствие двоичный набор согласно табл.15.1.
Далее, команде I машины Тьюринга Т, имеющей вид qa à q’a’d, ставится в соответствие двоичный набор вида
Код (I) = Код(q) Код(a) Код(q’) Код(a’) Код(d),
в котором коды букв приписаны друг к другу. Пусть машина Т имеет алфавиты A = {a0, a1, …, am} и Q = {q0, q1, …, qn}. Упорядочим команды машины Т в соответствии с лексикографическим порядком левых частей команд:
q1, a0, q1, a1, …, q1, am, q2, a0, …, q2, am, …, qn, a0, …, qn, am.
Пусть I1, …, In(m+1), — соответствующая последовательность команд. Тогда машине Т поставим в соответствие двоичный набор вида
Код(T) = Код(I1) Код(I2)… Код(In(m+1)),
полученный приписыванием друг к другу кодов команд.
Таблица 15.1
| Символ | Код | Число нулей в коде | |
| Символы сдвига | R L E | ||
| Символы алфавита ленты | a0 a1 … ai … | … 100…00 … | … 2×i + 4 … |
| Символы алфавита состояний | q0 q1 … qi … | … 100…00 … | … 2×j + 5 … |
Пример 15.1. Пусть дана машина Тьюринга Т. A = {a0, a1} и Q = {q0, q1}:
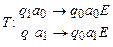 .
.
Тогда имеем Код(T) = 107104105104103107106105106103.
Легко видеть, что машина Т переводит конфигурации 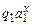 в конфигурации
в конфигурации 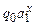 , и поэтому, представляя натуральное число n как
, и поэтому, представляя натуральное число n как 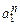 , получаем, что машина Т вычисляет функцию f(x) = x.
, получаем, что машина Т вычисляет функцию f(x) = x.
Ясно, что указанное кодирование является алгоритмической процедурой. Имея код машины, однозначно восстанавливается множество ее команд — для этого надо выделить подслова, начинающиеся с единицы с нулями до следующей единицы. Пятерка таких подслов образует команду. Далее, легко видеть, что имеется алгоритмическая процедура, позволяющая по произвольному слову из 0, 1 выяснять — будет ли это слово служить кодом некоторой машины Тьюринга. Будем теперь рассматривать код машины Тьюринга как двоичную запись натурального числа. Данное число назовем номером машины Тьюринга. Поскольку все коды начинаются с единицы, то разным кодам соответствуют разные числа. Упорядочим машины Тьюринга по возрастанию чисел, представляемых их кодами, и занумеруем их Т0, Т1, …, Тn, … .
Номер машины Т в этом упорядочении будем обозначать nT.
Указанное упорядочение является эффективным в том смысле, что существует алгоритм, который по n выдает Код(Tn) и существует алгоритм, который, наоборот, по Код(Tn) выдает nT.
Если обозначить через fn(x) одноместную функцию, которую вычисляет машина Тьюринга Tn, то в результате получим нумерацию всех одноместных частично рекурсивных функций:
f0(x), f1(x), …, fn(x), …
Согласно доказанному, каждая одноместная частично рекурсивная функция представлена в этой последовательности. Можно доказать, что каждая такая функция представлена в последовательности (5) бесконечное число раз. Аналогично можно определить нумерацию n-местных функций.
Дата добавления: 2022-05-27; просмотров: 199;











