Машина Тьюринга и функции, вычислимые по Тьюрингу
Опишем алгоритмическую модель, предложенную А. Тьюрингом в 30-х годах прошлого столетия и оказавшую влияние на разработку ЭВМ.
Машина Тьюринга состоит из следующих элементов:
1) ленты, разбитой на ячейки и бесконечной в обе стороны. В каждой ячейке может быть записан один из символов конечного алфавита 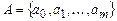 , называемого внешним алфавитом. Условимся считать, что символ
, называемого внешним алфавитом. Условимся считать, что символ 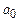 является пустым символом (также обозначаемым ^);
является пустым символом (также обозначаемым ^);
2) управляющего устройства, которое может находиться в одном из конечного числа внутренних состояний 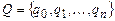 . Число элементов в Q характеризует объем внутренней памяти машины. В множестве Q выделены два специальные состояния:
. Число элементов в Q характеризует объем внутренней памяти машины. В множестве Q выделены два специальные состояния: 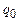 и
и 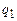 , называемые заключительным и начальным состояниями соответственно. Машина начинает работу в состоянии
, называемые заключительным и начальным состояниями соответственно. Машина начинает работу в состоянии 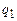 , попав в состояние
, попав в состояние 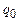 , машина всегда останавливается;
, машина всегда останавливается;
3) считывающей/пишущей головки, которая может перемещаться вдоль ленты и в каждый момент времени обозревает (считывает) одну из ячеек ленты. Функционирование машины Тьюринга осуществляется в дискретные моменты времени 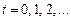 и заключается в следующем. В зависимости от внутреннего состояния машины и считываемого символа на ленте машина Тьюринга:
и заключается в следующем. В зависимости от внутреннего состояния машины и считываемого символа на ленте машина Тьюринга:
а) записывает в эту ячейку символ внешнего алфавита;
б) сдвигает считывающую головку на один шаг влево или один шаг вправо или оставляет ее на месте;
с) переходит в новое внутреннее состояние.
Таким образом, работа машины определяется системой команд вида
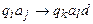 , (11.1)
, (11.1)
где 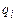 — внутреннее состояние машины;
— внутреннее состояние машины; 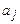 — считываемый символ;
— считываемый символ; 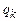 — новое внутреннее состояние;
— новое внутреннее состояние; 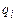 — новый записываемый символ; d — направление движения головки, обозначаемой одним из символов L (влево), R (вправо), Е (на месте).
— новый записываемый символ; d — направление движения головки, обозначаемой одним из символов L (влево), R (вправо), Е (на месте).
Предполагается, что для каждой пары 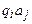 , где
, где 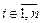 ,
, 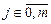 , имеется точно одна команда вида (11.1). Множество этих команд называется программой машины и, значит, в программе имеется n(m + 1) команд[4].
, имеется точно одна команда вида (11.1). Множество этих команд называется программой машины и, значит, в программе имеется n(m + 1) команд[4].
Работа машины заключается в изменении конфигураций. Конфигурация представляет собой совокупность внутреннего состояния, состояния ленты (т.е. размещения букв внешнего алфавита по ячейкам или слова, записанного на ленте), положения головки на ленте.
Предположим, что в начальный момент времени на ленте все ячейки, кроме конечного их числа, содержат пустой символ. Следовательно, и в любой другой момент времени лента будет иметь лишь конечное число ячеек, содержащих непустые символы.
Активной зоной конфигурации назовем минимальную связную часть ленты, содержащую обозреваемую ячейку, а также все ячейки, в которых записаны непустые символы.
Конфигурацию можно представить в виде машинного слова в алфавите 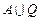 вида
вида 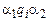 , где
, где 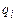 — внутреннее состояние,
— внутреннее состояние, 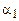 — слово из символов алфавита А, находящееся в левой части активной зоны от считывающей головки, a2 — слово из считываемого символа и символов алфавита А, находящегося в правой части активной зоны от считывающей головки. Конфигурация К называется заключительной, если
— слово из символов алфавита А, находящееся в левой части активной зоны от считывающей головки, a2 — слово из считываемого символа и символов алфавита А, находящегося в правой части активной зоны от считывающей головки. Конфигурация К называется заключительной, если 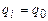 и начальной, если
и начальной, если 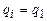 . Условимся, что стандартная начальная конфигурация имеет вид
. Условимся, что стандартная начальная конфигурация имеет вид 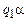 , а стандартная заключительная конфигурация имеет вид
, а стандартная заключительная конфигурация имеет вид 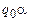 . Конфигурацию в момент времени t обозначим
. Конфигурацию в момент времени t обозначим 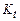 . Машина реализует процесс изменения конфигураций в следующем смысле. Если
. Машина реализует процесс изменения конфигураций в следующем смысле. Если 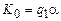 и
и 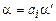 ,
, 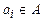 , то в программе машины имеется точно одна команда вида
, то в программе машины имеется точно одна команда вида 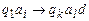 . Тогда следующая конфигурация
. Тогда следующая конфигурация 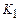 определяется так:
определяется так:
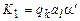 , если d = E;
, если d = E;
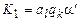 , если d = R;
, если d = R;
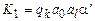 , если d = L.
, если d = L.
Это обстоятельство записываем в виде: 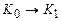 . Если теперь конфигурация
. Если теперь конфигурация 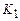 не является заключительной, то в соответствии с системой команд, аналогично предыдущему, определима однозначно следующая конфигурация
не является заключительной, то в соответствии с системой команд, аналогично предыдущему, определима однозначно следующая конфигурация 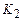 , т.е.
, т.е. 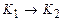 . Таким образом, начальная конфигурация
. Таким образом, начальная конфигурация 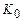 порождает последовательность конфигураций
порождает последовательность конфигураций 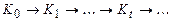 Если последовательность конечна, т.е. обрывается в заключительной конфигурации, то говорят, что машина применима к конфигурации
Если последовательность конечна, т.е. обрывается в заключительной конфигурации, то говорят, что машина применима к конфигурации 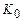 , в противном случае говорят, что машина неприменима к
, в противном случае говорят, что машина неприменима к 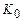 .
.
Если машина применима к конфигурации 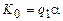 и
и 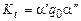 — заключительная конфигурация, то слово
— заключительная конфигурация, то слово 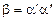 объявляется результатом работы машины на слове a. Таким образом, машине Тьюринга соответствует частичная словарная функция с областью определения и областью значения, являющейся конечными словами в алфавите А, которая каждому такому слову ставит в соответствие результат применения машины к данному слову.
объявляется результатом работы машины на слове a. Таким образом, машине Тьюринга соответствует частичная словарная функция с областью определения и областью значения, являющейся конечными словами в алфавите А, которая каждому такому слову ставит в соответствие результат применения машины к данному слову.
Потребуем, чтобы заключительные конфигурации машины находились в стандартной форме. Этого всегда можно добиться, добавляя к машине Т два новых состояния 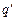 и
и 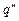 и команды:
и команды:
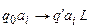 ,
, 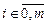 ;
;
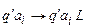 ,
, 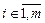 ;
;
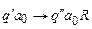 .
.
При этом состояние 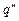 объявим заключительным. Полученная машина
объявим заключительным. Полученная машина 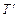 эквивалентна машине Т в следующем смысле:
эквивалентна машине Т в следующем смысле:
а) обе машины применимы к одним и тем же начальным конфигурациям;
б) результаты применения обеих машин совпадают;
с) заключительные конфигурации у машины 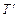 находятся в стандартной форме.
находятся в стандартной форме.
Определим теперь вычисление функций на машине Тьюринга. Будем рассматривать словарные частичные[5] функции f типа 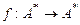 , где
, где 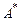 — множество всех слов конечной длины в алфавите А.
— множество всех слов конечной длины в алфавите А.
Говорят, что машина Тьюринга Т правильно вычисляет частичную функцию f для любого 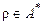 при условии:
при условии:
если 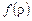 определено и
определено и 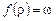 , то машина Т применима к начальной конфигурации
, то машина Т применима к начальной конфигурации 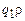 , и заключительной конфигурацией является
, и заключительной конфигурацией является 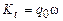 ;
;
если 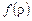 не определено, то машина Т неприменима к начальной конфигурации
не определено, то машина Т неприменима к начальной конфигурации 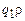 .
.
Функция f называется правильно вычислимой по Тьюрингу, если существует машина Тьюринга Т, которая ее правильно вычисляет.
Аналогичные определения могут быть сделаны и для функций нескольких переменных. Для этого достаточно множество слов, являющихся аргументами, записать в виде одного слова, введя знак-разделитель. Ограничимся соответствующим определением для числовых функций. Рассмотрим частичную функцию 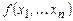 от n переменных, аргументы которой и ее значения принадлежат множеству
от n переменных, аргументы которой и ее значения принадлежат множеству 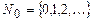 . Будем считать, что алфавит А машины Т содержит элемент 1. Условимся, произвольное число
. Будем считать, что алфавит А машины Т содержит элемент 1. Условимся, произвольное число 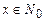 представлять в виде слова
представлять в виде слова 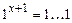 (x + 1 раз), чтобы запись нуля была непустой. Будем говорить, что машина Тьюринга Т правильно вычисляет функцию
(x + 1 раз), чтобы запись нуля была непустой. Будем говорить, что машина Тьюринга Т правильно вычисляет функцию 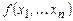 , если конфигурацию
, если конфигурацию 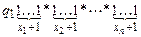 она переводит в конфигурацию
она переводит в конфигурацию 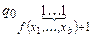 , если значение
, если значение 
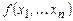 определено, и Т неприменима, если значение
определено, и Т неприменима, если значение 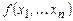 не определено. Здесь * — символ-разделитель из А. Класс функций, вычислимых по Тьюрингу обозначим через Т.
не определено. Здесь * — символ-разделитель из А. Класс функций, вычислимых по Тьюрингу обозначим через Т.
Рассмотрим несколько примеров на построение машин Тьюринга.
1. Пусть 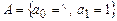 ,
, 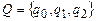 . Программа машины
. Программа машины 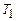 :
:
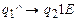 ;
;
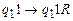 ;
;
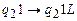 ;
;
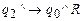 .
.
Пусть 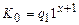 . Тогда
. Тогда 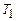 правильно вычисляет функцию
правильно вычисляет функцию 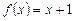 ,
, 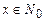 .
.
2. Пусть 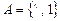 ,
, 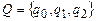 . Программа машины
. Программа машины 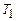 :
:
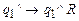 ;
;
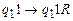 ;
;
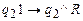 ;
;
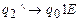 .
.
Пусть 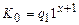 . Тогда
. Тогда 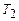 правильно вычисляет функцию
правильно вычисляет функцию 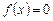 ,
, 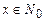 .
.
3. Пусть 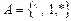 ,
, 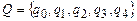 . Программа машины
. Программа машины 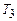 :
:
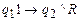 ;
;
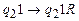 ;
;
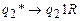 ;
;
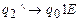 ;
;
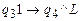 ;
;
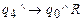 ;
;
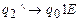 .
.
Пусть 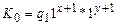 . Тогда
. Тогда 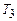 правильно вычисляет функцию
правильно вычисляет функцию 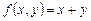 ,
, 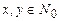 .
.
Прямое построение машин Тьюринга для решения даже простых задач может оказаться затруднительным. Однако существуют приемы, которые облегчают данный процесс, если использовать способы сочетания программ нескольких машин в результирующие программы. Дадим некоторое представление об этих приемах, что позволит говорить о существовании тех или иных машин, на деталях же построения конкретных программ останавливаться не будем.
Суперпозиция машин. Пусть даны две машины Тьюринга 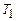 и
и 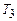 , которые вычисляют, соответственно, словарные функции
, которые вычисляют, соответственно, словарные функции 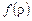 и
и 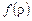 в одном и том же алфавите. Тогда существует машина Тьюринга Т, которая вычисляет функцию
в одном и том же алфавите. Тогда существует машина Тьюринга Т, которая вычисляет функцию 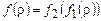 . При этом для любого слова
. При этом для любого слова 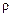 функция
функция 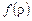 определена в том и только в том случае, когда
определена в том и только в том случае, когда 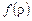 определена и
определена и 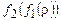 определена. Программа машины Т строится так. Состояния машины
определена. Программа машины Т строится так. Состояния машины 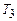 переобозначаем так, чтобы они отличались от состояний машины
переобозначаем так, чтобы они отличались от состояний машины 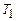 . Начальное состояние
. Начальное состояние 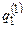 машины
машины 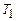 объявляем начальным
объявляем начальным 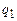 для машины Т, заключительное состояние
для машины Т, заключительное состояние 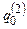 машины
машины 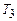 объявляем заключительным q0 для машины Т. Заключительное состояние
объявляем заключительным q0 для машины Т. Заключительное состояние 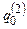 машины
машины 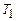 отождествляем с начальным состоянием
отождествляем с начальным состоянием 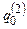 машины T2. Полученные команды для обеих машин объединяем в одну программу. Рассмотрим начальную конфигурацию
машины T2. Полученные команды для обеих машин объединяем в одну программу. Рассмотрим начальную конфигурацию 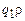 . Поскольку
. Поскольку 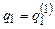 — начальное состояние машины T1, то вначале Т работает как машина T1, и если T1 применима к
— начальное состояние машины T1, то вначале Т работает как машина T1, и если T1 применима к 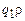 , то на некотором шаге будет получена конфигурация
, то на некотором шаге будет получена конфигурация 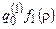 , но
, но 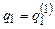 — начальное состояние для T2, и теперь Т действует как машина T2. Если T2 применима к
— начальное состояние для T2, и теперь Т действует как машина T2. Если T2 применима к 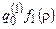 , то на некотором шаге будет получена конфигурация
, то на некотором шаге будет получена конфигурация 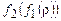 , которая является заключительной для Т, так как
, которая является заключительной для Т, так как 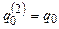 . Если T1 неприменима к
. Если T1 неприменима к 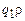 или T2 неприменима к
или T2 неприменима к 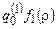 , то Т неприменима к
, то Т неприменима к 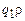 . Машина Т называется суперпозицией машин T1 и T2 и обозначается
. Машина Т называется суперпозицией машин T1 и T2 и обозначается 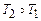 .
.
Схематически суперпозиция изображается так:
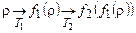 .
.
Соединение машин. Пусть даны машины Тьюринга T1 и T2, вычисляющие словарные функции 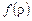 и
и 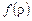 соответственно. Тогда существует машина Т, которая начальную конфигурацию
соответственно. Тогда существует машина Т, которая начальную конфигурацию 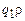 переводит в заключительную
переводит в заключительную 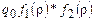 , если
, если 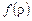 и
и 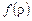 определены, и неприменима в противном случае. Здесь * — новый символ, не входящий в алфавиты машин T1 и T2. Машина Т называется соединением машин и обозначается T1* T2. Существование машины Т вытекает из следующих неформально описываемых конструкций. Лента машины Т является двухэтажной. В качестве внешнего алфавита Т берутся двухэтажные буквы
определены, и неприменима в противном случае. Здесь * — новый символ, не входящий в алфавиты машин T1 и T2. Машина Т называется соединением машин и обозначается T1* T2. Существование машины Т вытекает из следующих неформально описываемых конструкций. Лента машины Т является двухэтажной. В качестве внешнего алфавита Т берутся двухэтажные буквы 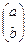 , где a, b — буквы алфавитов T1 и T2. Каждой букве a ставится в соответствие двухэтажная буква
, где a, b — буквы алфавитов T1 и T2. Каждой букве a ставится в соответствие двухэтажная буква 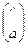 . Слову
. Слову 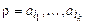 ставится в соответствие двухэтажное слово
ставится в соответствие двухэтажное слово 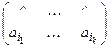 . Машина Т будет работать так (существование машин Тьюринга для реализации каждого шага ясно):
. Машина Т будет работать так (существование машин Тьюринга для реализации каждого шага ясно):
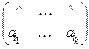 ®
® 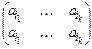 ®
® 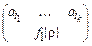 ®
®
® 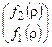 ®
® 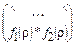 .
.
Ветвление машин. Пусть даны машины Тьюринга T1 и T2, вычисляющие словарные функции 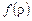 и
и 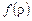 соответственно, заданные в одном алфавите. Тогда существует машина Тьюринга Т, которая начальную конфигурацию
соответственно, заданные в одном алфавите. Тогда существует машина Тьюринга Т, которая начальную конфигурацию 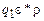 , где
, где 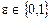 , переводит в заключительную
, переводит в заключительную 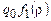 , если e = 0 и в
, если e = 0 и в 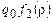 , если e = 1. Машина Т называется разветвлением машин T1 и T2 и обозначается T1 Ú T2. Схематически разветвление представляется так:
, если e = 1. Машина Т называется разветвлением машин T1 и T2 и обозначается T1 Ú T2. Схематически разветвление представляется так:
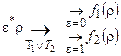 .
.
Существование машины Т вытекает из следующих конструкций. Пусть 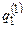 и
и 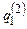 — начальные состояния машин T1 и T2 соответственно. Считаем, что множества внутренних состояний машин не пересекаются. Объединим программы машин T1 и T2, добавим новое начальное состояние
— начальные состояния машин T1 и T2 соответственно. Считаем, что множества внутренних состояний машин не пересекаются. Объединим программы машин T1 и T2, добавим новое начальное состояние 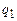 и добавим команды:
и добавим команды:
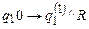 ;
;
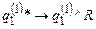 ;
;
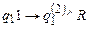 ;
;
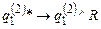 .
.
Теперь заключительные состояния 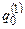 и
и 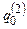 машин T1 и T2 объединим, а полученное состояние
машин T1 и T2 объединим, а полученное состояние 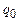 будем считать заключительным для Т. Если
будем считать заключительным для Т. Если 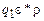 — начальная конфигурация, то Т через 2 шага перейдет в конфигурацию
— начальная конфигурация, то Т через 2 шага перейдет в конфигурацию 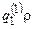 , если e = 0, и вконфигурацию
, если e = 0, и вконфигурацию 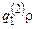 , если e = 1, а затем будет работать как T1 или T2 соответственно.
, если e = 1, а затем будет работать как T1 или T2 соответственно.
Реализация цикла. Важным приемом в программировании является разбиение решаемой задачи на циклы. После выполнения каждого цикла проверяется выполнимость некоторого условия. Если условие выполнено, то выдается результат, если нет, то цикл повторяется. Точнее, процедура задается так. Пусть имеем словарные функции 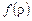 и
и 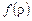 и некоторый предикат Ф на словах (его значения обозначим 0,1). Для произвольного слова r проверяется — верно ли Ф(r) = 1, если да, то выдается ответ
и некоторый предикат Ф на словах (его значения обозначим 0,1). Для произвольного слова r проверяется — верно ли Ф(r) = 1, если да, то выдается ответ 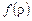 . Если Ф(r) = 0, то вычисляется
. Если Ф(r) = 0, то вычисляется 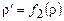 . Затем проверяется — верно ли
. Затем проверяется — верно ли 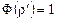 , если да, то выдается ответ
, если да, то выдается ответ 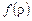 . Если
. Если 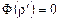 , то вычисляется
, то вычисляется 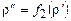 и т.д. Существует машина Тьюринга Т, реализующая данную процедуру. Пусть существуют машины Тьюринга для вычисления функций
и т.д. Существует машина Тьюринга Т, реализующая данную процедуру. Пусть существуют машины Тьюринга для вычисления функций 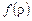 и
и 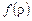 и предиката Ф. Обозначим их T1, T2 и
и предиката Ф. Обозначим их T1, T2 и 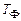 соответственно. Пусть T0 — машина, которая оставляет всякое слово r без изменения. Машина Т строится в соответствии со схемой:
соответственно. Пусть T0 — машина, которая оставляет всякое слово r без изменения. Машина Т строится в соответствии со схемой:
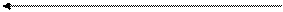 r
r 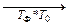
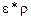
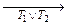
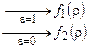
Пояснение: Заключительные состояния 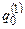 и
и 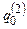 машин T1 и T2 не объединяются, а считаются различными. Состояние
машин T1 и T2 не объединяются, а считаются различными. Состояние 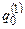 объявляется заключительным для Т, а
объявляется заключительным для Т, а 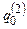 отождествляется с начальным состоянием
отождествляется с начальным состоянием 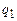 для Т. Заключительное состояние для машины
для Т. Заключительное состояние для машины 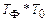 объявляется начальным для T1 Ú T2. Из изложенного следует, что если T1 Ú T2 работает как T1, то полученное ею значение является выходом Т, если же T1 Ú T2 работает как T2, то полученное ею значение снова подается на вход машины Т. Используя данный прием, можно построить машину Тьюринга для перевода произвольного числа n ³ 1, заданного в унарной записи, т.е. в виде 1n + 1, в его двоичную запись, начинающуюся с 1.
объявляется начальным для T1 Ú T2. Из изложенного следует, что если T1 Ú T2 работает как T1, то полученное ею значение является выходом Т, если же T1 Ú T2 работает как T2, то полученное ею значение снова подается на вход машины Т. Используя данный прием, можно построить машину Тьюринга для перевода произвольного числа n ³ 1, заданного в унарной записи, т.е. в виде 1n + 1, в его двоичную запись, начинающуюся с 1.
Входной алфавит машины есть 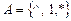 . Вначале стирается одна палочка, затем работа осуществляется с циклами
. Вначале стирается одна палочка, затем работа осуществляется с циклами 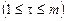 . К концу каждого цикла t машина находится в конфигурации
. К концу каждого цикла t машина находится в конфигурации
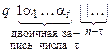 .
.
В течение цикла t стирается одна палочка и к числу t – 1 в двоичной записи прибавляется 1. Формальное описание машины Тьюринга, однако, требует большого числа технических деталей, и поэтому мы их опускаем.
Таким образом, язык тьюрингова программирования содержит основные операторы программирования на алгоритмических языках и позволяет устраивать последовательное выполнение программ, параллельное их соединение, использовать условные переходы («если Ф, выполнить f1, иначе f2»), реализовывать цикл («пока Ф, выполнять f1, иначе f2»). Это является основанием для предположения о том, что для всех процедур, претендующих называться алгоритмическими, существует (при подходящем кодировании) реализующая их машина Тьюринга. Данное предположение носит название тезиса Тьюринга.
Данный тезис доказать нельзя, поскольку здесь используется интуитивное понятие алгоритма. Подтверждением тезису является математическая практика, а также то, что описание алгоритма в любой другой алгоритмической модели может быть сведено к описанию его в виде машины Тьюринга. Однако принятие тезиса Тьюринга позволяет истолковывать утверждения о несуществовании машин Тьюринга для решения конкретных задач как утверждения о несуществовании алгоритмов вообще.
Дата добавления: 2022-05-27; просмотров: 204;











