Описание алгоритма умножения чисел с ПЗ
В качестве основной операции выступает операция умножения двоичных чисел первым способом в прямом коде (ПК) с плавающей запятой (ПЗ), с характеристикой. Главной особенностью данного способа умножения является возможность использования n-разрядных регистров для хранения мантисс операндов и результата и, соответственно, n-разрядного сумматора мантисс.
Алгоритм состоит из следующих пунктов:
1. Определить знак произведения сложением по модулю два знаковых разрядов сомножителей, и далее использовать модули операндов.
2. Проверить множимое на равенство нулю: если равно нулю, операцию умножения следует прекратить, т.к. результат будет также равным нулю.
3. Проверить множитель на равенство нулю: если равен нулю, операцию умножения следует прекратить, т.к. результат будет также равным нулю.
4. Сложить характеристики сомножителей. При этом могут возникнуть следующие ситуации: переполнение разрядной сетки (ПРС), временное ПРС или потеря младших разрядов (ПМР). Если возникло ПРС (признаком ПРС является получение единицы переноса и единицы в старшем разряде результирующей характеристики), то необходимо зафиксировать её появление и прекратить операцию. Временное ПРС может возникнуть, когда в старший разряд равен единице, образовалась единица переноса, но все разряды характеристики, за исключением старшего, равны нулю. При этом нужно продолжить алгоритм умножения. Если возникла ситуация ПМР (признаком ПМР является отсутствие единицы переноса и ноль в старшем разряде результирующей характеристики), то необходимо зафиксировать её появление и выдать нулевой результат. В противном случае переходим к пункту 5.
5. Анализ младшей цифры очередного разряда множителя: если цифра множителя «1», то суммировать множимое с накопленной суммой частичных произведений (ЧП). В результате суммирования может возникнуть ситуация временного ПРС в мантиссе, которая устраняется последующим сдвигом вправо.
6. Выполнить в основном цикле - сложение мантисс операндов и сдвиги: множителя на один разряд вправо, сумы частичных произведений на один разряд влево.
7. После цикла умножения необходимо провести проверку на необходимость нормализации результата. Если произведение денормализовано, провести нормализацию результата: сдвинем произведение на 1 разряд влево, вычтем “1” из характеристики. При этом, если ранее было зафиксировано временное ПРС, оно устраняется. Если после нормализации мантиссы произошло ПМР, нужно зафиксировать её появление и вывести результат равный «0»; в противном случае переходим к пункту 8.
Денормализация возможна лишь на один разряд, т.к. операнды поступают на входную шину уже нормализованными. Если результат нормализован, необходимо проверить, было ли зафиксировано временно ПРС. Если да, то установить признак ПРС и операцию необходимо прекратить.
8. Присвоить знак модулю произведения из п. 1 алгоритма. Если после нормализации результата зафиксирован признак ПМР, то в качестве знака результата необходимо выдать ноль.
Численный пример
Рассмотрим алгоритм умножения на числовом примере:
А = -2,37510 = 1,10010 100110002
В = 0,17187510 = 1,01110 101100002
1) 1 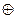 0 = 1
0 = 1
2) Суммируем характеристики
1,0010
0,1110
10,0000
ПРС и ПМР не возникло.
3) Последовательность операций умножения представлена в табл. 3
Таблица 3 – Умножение двоичных чисел первым способом с ПЗ
| Множитель | Сумма ЧП | Комментарии |
| 0,10011000 | 0,00000000 00000000 | Сдвиг вправо |
| 0,01001100 | 0,00000000 00000000 | Сдвиг вправо |
| 0,00100110 | 0,00000000 00000000 | Сдвиг вправо |
| 0,00010011 | 0,00000000 00000000 0,10110000 0,10110000 00000000 | Сложение Сдвиг вправо |
| 0,00001001 | 0,01011000 00000000 0,10110000 1,00001000 00000000 (временное ПРС) | Сложение Сдвиг вправо |
| 0,00000100 | 0,10000100 00000000 | Сдвиг вправо |
| 0,00000010 | 0,01000010 00000000 | Сдвиг вправо |
| 0,00000001 | 0,00100001 00000000 0,10110000 0,11010001 00000000 | Сложение Сдвиг вправо |
| 0,00000000 | 0,01101000 10000000 |
Сумма ЧП = 0,01101000 10000000 – требуется нормализация. Сдвинем результат на 1 разряд влево, и вычтем единицу из суммы характеристик.
0,0000
 1,1111
1,1111
1,1111 0,1111 (-1) - ПМР не возникло.
Результат: 1,01111 110100012 = -0,40820310
Проверка -2,375 * 0,171875 = -0,408203
Дата добавления: 2022-02-05; просмотров: 530;











