Передаточная функция ПК интегратора без задержки

Перепишем выражение (1.42):

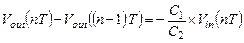(1.55)

Второй член в левой части, соответствующий потенциалу, хранящемуся на интегрирующем конденсаторе с момента 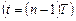, в этом уравнении формально как бы задержанна период Т до момента 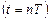начала изменения потенциала 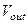на выходе ПК интегратора. Вследствие этого после z-преобразования выражения (1.55) и представления каждого слагаемого в функции от z, задержанное слагаемое будет отличаться от НЕ задержанных множителем :

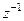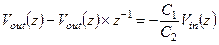(1.56)

Из (1.56) получаем передаточную функцию ПК интегратора без задержки:

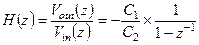(1.57)

Передаточная функция ПК интегратора с задержкой

Перепишем выражение (1.47b):

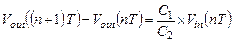(1.58)

При использовании доводов, приведенных в предыдущем разделе, после z-преобразования выражения (1.58) можно записать:

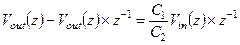(1.59)

Из (1.59) получаем передаточную функцию ПК интегратора с задержкой:

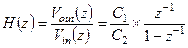(1.60)

z-преобразование используется в методах анализа и синтеза систем, как цифровых, так и аналоговых, работающих в режиме дискретного времени. Изложение этих методов представлено в пособии «Проектирование ИМС смешанного сигнала».