Интегральное уравнение теплоотдачи для стабилизированного теплообмена
Рассмотрим приближенный метод определения коэффициентов теплоотдачи при гидродинамически и термически стабилизированном течении жидкости в прямой круглой трубе.
Будем полагать, что жидкость несжимаема, ее физические параметры постоянны, теплотой трения можно пренебречь, внутренние источники теплоты отсутствуют.
Уравнение энергии для осесимметричного стационарного потока можно записать следующим образом:
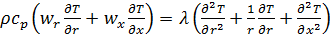 .
.
Уравнение записано в цилиндрических координатах, где 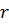 –текущий радиус,
–текущий радиус, 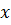 – продольная координата, направленная по оси трубы в сторону движения жидкости.
– продольная координата, направленная по оси трубы в сторону движения жидкости.
Будем полагать, что перенос теплоты теплопроводностью в радиальном направлении много больше, чем в осевом. Тогда членом 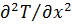 можно пренебречь. Кроме того,
можно пренебречь. Кроме того, 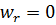 . Учтем, что в турбулентном потоке теплота переносится не только теплопроводностью, но и путем турбулентных пульсаций. Уравнение энергии при этом может быть записано в следующем виде:
. Учтем, что в турбулентном потоке теплота переносится не только теплопроводностью, но и путем турбулентных пульсаций. Уравнение энергии при этом может быть записано в следующем виде:
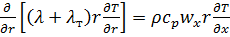 ,
,
где 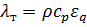 –коэффициент турбулентного переноса теплоты;
–коэффициент турбулентного переноса теплоты; 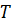 и
и 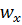 – осредненные во времени местные значения температуры и скорости турбулентного потока.
– осредненные во времени местные значения температуры и скорости турбулентного потока.
Назначим граничное условие 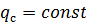 . Как было показано в гл.6, при
. Как было показано в гл.6, при 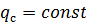
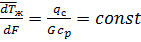 .
.
Для круглой трубы 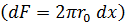
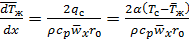 ,
,
где 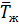 – среднемассовая температура жидкости в данном сечении;
– среднемассовая температура жидкости в данном сечении; 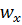 – средняя скорость в этом же сечении;
– средняя скорость в этом же сечении; 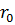 – радиус трубы.
– радиус трубы.
В рассматриваемых условиях средняя температура жидкости будет линейной функцией 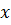 . При
. При 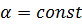 по линейному закону изменяется не только
по линейному закону изменяется не только 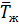 , но и температура стенки:
, но и температура стенки:
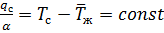 .
.
При неизменных физических свойствах местная температура жидкости изменяется вдоль трубы также по линейному закону. Отсюда следует:
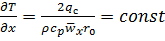 .
.
Подставляя выражение для 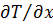 в уравнение энергии, получаем:
в уравнение энергии, получаем:
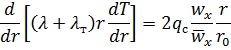
или
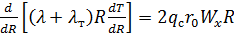 ,
,
где 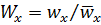 и
и 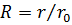 – соответственно безразмерные скорость и радиус.
– соответственно безразмерные скорость и радиус.
Разделяя переменные и интегрируя в пределах от 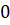 до
до 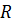 и от
и от 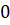 до
до 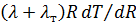 , получаем:
, получаем:
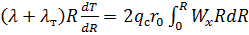 .
.
Отсюда следует, что
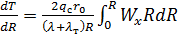 . (a)
. (a)
Среднемассовая температура жидкости при постоянных 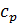 и
и 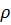 определяется уравнением
определяется уравнением
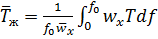 .
.
Так как для круглой трубы 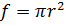 и
и 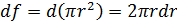 , то
, то
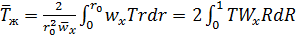 .
.
Найдем этот интеграл по частям. Формула интегрирования по частям:
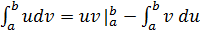 .
.
Обозначим
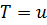 и
и 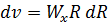 или
или 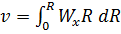 ,
,
тогда
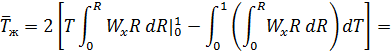
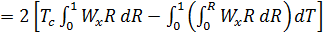 . (б)
. (б)
Интеграл 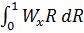 может быть преобразован следующим образом:
может быть преобразован следующим образом:
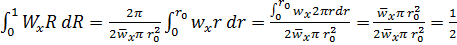 .
.
Подставляя полученное значение интеграла в (б), получаем:
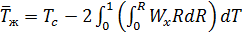 .
.
После подстановки сюда значения 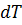 согласно уравнению (а) можно написать:
согласно уравнению (а) можно написать:
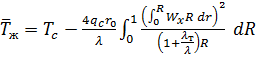 ;
;
отсюда следует:
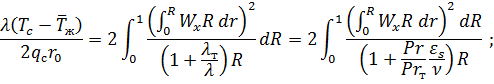
где 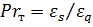 –турбулентное число Прандтля.
–турбулентное число Прандтля.
Согласно определению
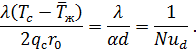
Используя последнее обозначение, можно написать следующее интегральное уравнение теплоотдачи для стабилизированного теплообмена:
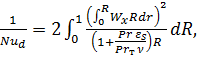 (7.3)
(7.3)
Уравнение (7.3) было получено Лайоном. Оно пригодно как для турбулентного, так и для ламинарного течения. Если известно распределение скоростей 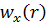 , то с помощью уравнения (7.3) можно рассчитать коэффициенты теплоотдачи.
, то с помощью уравнения (7.3) можно рассчитать коэффициенты теплоотдачи.
Для ламинарного течения 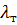 =0 и уравнение (7.3) упрощается:
=0 и уравнение (7.3) упрощается:
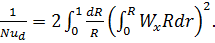 (8.3’)
(8.3’)
Дата добавления: 2016-06-05; просмотров: 1988;










