Гидравлическое сопротивление двухфазных потоков
Полный перепад давления. В инженерной практике используются, как правило, одномерные модели двухфазных потоков.
Перепад давления в направлении оси канала 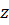 для одномерного двухфазного потока выражается уравнением:
для одномерного двухфазного потока выражается уравнением:
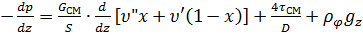 (11.30)
(11.30)
где 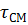 – касательное напряжение на стенке канала при течении смеси;
– касательное напряжение на стенке канала при течении смеси;
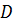 - гидравлический диаметр канала;
- гидравлический диаметр канала;
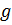 - проекция ускорения свободного падения на направление
- проекция ускорения свободного падения на направление 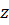 .
.
Первый член уравнения (11.30) отражает потери давления за счет ускорения потока, связанного либо с изменением паросодержания 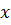 , либо с изменением площади поперечного сечения канала
, либо с изменением площади поперечного сечения канала 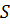 . При адиабатном течении в канале постоянного сечения этот член уравнения равен нулю.
. При адиабатном течении в канале постоянного сечения этот член уравнения равен нулю.
Второй и третий члены правой части уравнения (11.30) выражают соответственно потери давления на трение и на работу против массовых сил. При умеренных скоростях основной вклад в гидравлическое сопротивление вносят потери на трение.
Гомогенная модель дает простой, физически ясный и дающий удовлетворительные результаты метод расчета значений 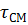 . В этом случае двухфазный поток рассматривается как однородная жидкость с плотностью
. В этом случае двухфазный поток рассматривается как однородная жидкость с плотностью 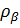 и средней скоростью течения
и средней скоростью течения 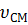 . Тогда:
. Тогда:
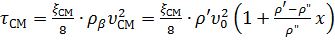 (11.31)
(11.31)
где 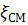 – коэффициент трения в пузырьковом, снарядном и эмульсионном режимах течения рассчитывается как для однофазного потока по формулам Блазиуса, Конакова, Шифринсона, Никурадзе и Альтшуля. При этом число Рейнольдса можно приближенно рассчитывать как
– коэффициент трения в пузырьковом, снарядном и эмульсионном режимах течения рассчитывается как для однофазного потока по формулам Блазиуса, Конакова, Шифринсона, Никурадзе и Альтшуля. При этом число Рейнольдса можно приближенно рассчитывать как 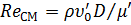 . При турбулентном течении удовлетворительные результаты получаются, если принять
. При турбулентном течении удовлетворительные результаты получаются, если принять 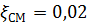 , что соответствует развитому турбулентному течению жидкости в гладких трубах.
, что соответствует развитому турбулентному течению жидкости в гладких трубах.
Формулу (11.31) можно представить в следующем виде:
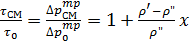 (11.32)
(11.32)
где 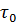 – касательное напряжение на стенке при течении в том же канале однофазной жидкости с расходом
– касательное напряжение на стенке при течении в том же канале однофазной жидкости с расходом 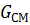 ;
;
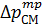 ,
, 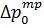 - перепады давления в канале за счет трения в двухфазном и однофазном потоках (
- перепады давления в канале за счет трения в двухфазном и однофазном потоках ( 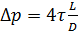 , где
, где 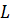 –длина канала,
–длина канала, 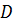 –диаметр канала).
–диаметр канала).
Согласно гомогенной модели потери на трение в двухфазном потоке с увеличением паросодержания растут линейно и при полном испарении жидкости 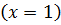 :
:
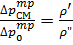 (11.33)
(11.33)
Применение формул (11.31) и (11.32) оправдано в потоках с гомогенной структурой, т.е. при пузырьковом и эмульсионном режимах течения, при 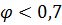 при больших скоростях смеси. При малых скоростях смеси дают заниженные значения
при больших скоростях смеси. При малых скоростях смеси дают заниженные значения 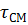 . Лучший результат достигается при расчете
. Лучший результат достигается при расчете 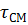 по формуле:
по формуле:
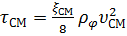 (11.34)
(11.34)
Причем плотность смеси рассчитывается по формуле:
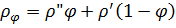 (11.35)
(11.35)
а истинное паросодержание по формулам:
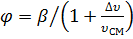 или
или 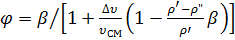 .
.
Дата добавления: 2016-06-05; просмотров: 3102;











