Расчет теплообменных аппаратов

Целью теплового расчета является определение поверхности теплообмена, а если последняя известна, то целью расчета является определение конечных температур рабочих жидкостей. Основными расчетными уравнениями теплообмена при стационарном режиме являются уравнение теплопередачи и уравнение теплового баланса. Уравнение теплопередачи:

Q = k·F·(t₁ – t₂ ) ,

где Q — тепловой поток, Вт, k - средний коэффициент теплопередачи, Вт/(м²град), F — поверхность теплообмена в аппарате, м², t₁ и t₂ - соответственно температуры горячего и холодного теплоносителей.

Уравнение теплового баланса при условии отсутствия тепловых потерь и фазовых переходов:

Q = = m₁ ·Dt₁ = m₂·Dt₂ ,

или

Q = V₁r₁·c_р1·(t^/₁ - t^//₁) = V₂ r₂·c_р2 ·(t^//₂ - t^/₂), (12.16)

где V₁r₁,V₂ r₂ - массовые расходы теплоносителей, кг/сек, с

c_р1 и c_р2 - средние массовые теплоемкости жидкостей в интервале температур от t^ґ до t^//,

t^/₁ и t^//₁ температуры жидкостей при входе в аппарат;

t^/₂ и t^//₂ - температуры жидкостей при выходе из аппарата.

Величину произведения

V·r·c_р = W, Вт/град

называют водяным, или условным, эквивалентом.

С учетом последнего уравнение теплового баланса может быть представлено в следующем виде:

(t^/₁ - t^//₁) / (t^//₂ - t^ґ₂) = W₂ / W₁ , (12.17 )

W₂ , W₁ - условные эквиваленты горячей и холодной жидкостей.

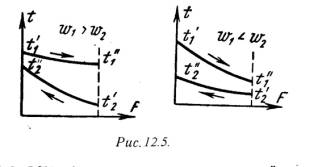
При прохождении через теплообменный аппарат рабочих жидкостей изменяются температуры горячих и холодных жидкостей. На изменение температур большое влияние оказывают схема движения жидкостей и величины условных эквивалентов. На рис.12.4 представлены температурные графики для аппаратов с прямотоков, а на рис.12.5 для аппаратов с противотоком.

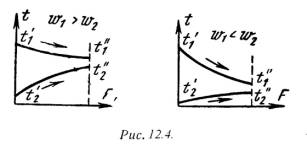
Как видно из рис.12.4 , при прямотоке конечная температура холодного теплоносителя всегда ниже конечной температуры горячего теплоносителя. При противотоке (рис.12.5) конечная температура холодной жидкости может быть значительно выше конечной температуры горячей жидкости. Следовательно, в аппаратах с противотоком можно нагреть холодную среду, при одинаковых начальных условиях, до более высокой температуры, чем в аппаратах с прямотоком. Кроме того, как видно из рисунков, наряду с изменениями температур изменяется также и разность температуря между рабочими жидкостями, или температурный напор Dt.

Величины Dt и k можно принять постоянными только в пределах элементарной поверхности теплообмена dF. Поэтому уравнение теплопередачи для элемента поверхности теплообмена dF справедливо лишь в дифференциальной форме:

dQ==k·dF·Dt . (12.18)

Тепловой поток, переданный через всю поверхность F при постоянном среднем коэффициенте теплопередачи k, определяется интегрированием уравнения (12. ):

Q = ò k·dF·Dt= k·F·Dt_ср , (12.19)

где Dt_ср - средний логарифмический температурный напор по всей поверхности нагрева.

Для случаев, когда коэффициент теплопередачи на отдельных участках поверхности теплообмена значительно изменяется, его усредняют:

k_ср = (F₁·k₁ + F₂·k₂ + … + F_n·k_n) / (F₁ + F₂ + … + F_n).

Тогда при k_ср = const уравнение (12.9 ) примет вид

Q = òk_ср Dt ·dF = k_ср ·Dt_ср ·F. (12.20)

Если температура теплоносителей изменяется по закону прямой линии (рис.12.6, пунктирные линии), то средний температурный напор в аппарате равен разности среднеарифметических величин:

Dt_ср = (t^/₁ + t^//₁)/2 - (t^//₂ + t^/₂)/2 . (12.21)

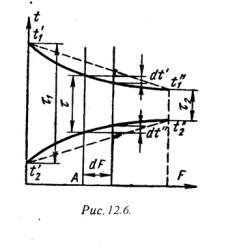
Однако температуры рабочих жидкостей меняются по криволинейному закону. Поэтому уравнение (12.21) будет только приближенным и может применяться при небольших изменениях температуры обеих жидкостей. При криволинейном изменении температуры величину Dt_ср называют среднелогарифмическим температурным напором и определяется по формулам:

для аппаратов с прямотоком

Dt_ср = [(t^/₁ - t^/₂) - (t^//₁ - t^//₂)] / ln[(t^/₁ - t^/₂)/(t^//₁ - t^//₂)] . (12.22)

для аппаратов с противотоком

Dt_ср = [(t^/₁ - t^//₂) - (t^//₁ - t^/₂)] / ln[(t^/₁ - t^//₂)/(t^//₁ - t^/₂)] . (12.23)

Численные значения Dt_ср для аппаратов с противотокм при одинаковых условиях всегда больше Dt_ср для аппаратов с прямотоком, поэтому аппараты с противотокм имеют меньшие размеры.

Литература

1. Лариков Н.Н. Теплотехника: Учебник для вузов. -3-е изд., перераб. и дополн.-М.; Стройиздат, 1985 -432 с.ил.
2. Нащокин В.В. Техническая термодинамика и теплопередача. -М.; Высшая школа, 1969 -560с.
3. Луканин В.Н., Шатров М.Г., Камфер Г.М. и др. Теплотехника: Учебник для вузов. –М.; Высш.шк., 1999.-671 с.ил.
4. Кудинов В.А., Карташов Э.М. Техническая термодинамика. –М.; Высш.шк., 2000. –261 с.ил.
5. Тихомиров К.В. Теплотехника, теплоснабжение и вентиляция. -М.; Стройиздат, 1981-248с.
6. Кириллин В.А., Сычев В.В., Шейндлин А.Е. Техническая термодинамика. -М.; Энергоиздат, 1983.
7. Исаченко В.М., Осипова В.А., Сухомел А.С. Теплопередача. -М.; Энергоиздат, 1981.
8. Михеев М.А., Михеева И.М. Основы теплопередачи. -М.; Энергия, 1977.
9. Теплоснабжение /Под ред. Ионина -М.; Стройиздат, 1982.
10. Теплотехника /Хазен М.М., Матвеев Г.А. и др. -М.; 1981.
11. Панкратов Г.П. Сборник задач по теплотехнике. М.; Высш. шк., 1986. -248с.
12. Сб. задач по технической термодинамике и теплопередаче /Дрыжаков Е.В., Исаев С.И. и др. -М.; 1968.
13. Сб. задач по технической термодинамике /Андрианов Т.А., Дзампов Б.В. и др. -М.; 1971.
14. Краснощеков Е.А., Сухомел А.С. Задачник по теплопередаче. -М.; 1975.
15. Балахонцев Е.В., Верес А.А. Теплотехника (методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений). М.; Высш. шк., 1985. –64 с.