Двигатели с электромагнитной редукцией

Индукторные машины известны более 100 лет, однако, применялись они в основном в качестве высокочастотных генераторов. Очевидно, что, используя свойство обратимости электрических машин, можно в двигательном режиме получить весьма низкие скорости вращения.

Принцип работы и основные соотношения параметров двигателей с электромагнитной редукцией (в дальнейшем будем называть индукторными) рассмотрим на основе метода гармонических зубцовых проводимостей, предложенного профессором А.И. Вольдеком для исследования полей в асинхронных машинах.

Пусть на статоре и на роторе имеют место открытые пазы, а левые грани 1–го зубца статора и 1–го зубца ротора совпадают (рис.6.4,а). Этому положению соответствует диаграмма удельной магнитной проводимости зазора 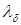(проводимости на единицу длины машины), изображенная в виде прямоугольников с шириной, равной зубцовым перекрытиям (рис. 6.4,б). Повернем ротор на угол 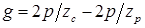, при котором совпадут левые грани двух следующих зубцов статора и ротора (рис. 6.4, а’). Диаграмм проводимости сместится на угол 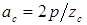(рис. 6.4,б’), который может быть значительно больше угла поворота ротора. Таким образом, мы получили двигатель, скорость вращения которого значительно меньше скорости вращения магнитного поля статора.

Проведя огибающую усредненных значений проводимостей (штриховые линии на рис. 6.4,б и б’), получим периодическую кривую, содержащую постоянную составляющую и переменную с числом периодов (пар полюсов) 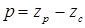. Если разложить кривую 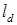в ряд Фурье, ограничиться постоянной составляющей ld0 и первой зубцовой гармоникой проводимости 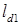(рис. 6.4,в), то удельную проводимость можно представить в следующем виде [6]:

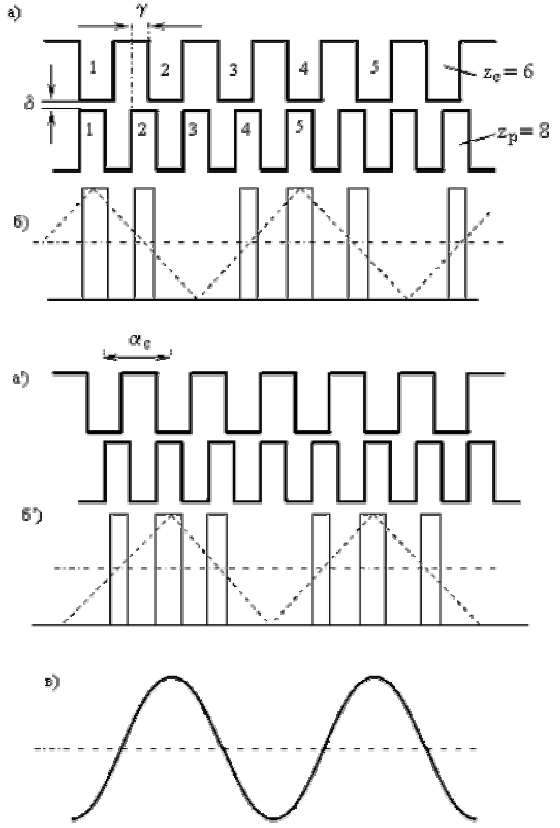
Рис. 6.4. К вопросу о принципе электромагнитной редукции

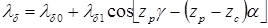. (6.4)

где 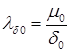– удельная магнитная проводимость равномерного воздушного зазора; 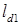– амплитуда первой зубцовой гармоники проводимости при двухсторонней зубчатости статора и ротора; 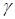– угол смещения ротора; 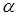– угловая координата.

При равномерном вращении ротора с угловой скоростью 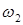угол смещения 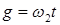. Для определения угловой скорости вращения гармоники проводимости приравняем к постоянной величине аргумент тригонометрической функции

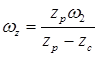
Продифференцировав это равенство по t и принимая во внимание, что 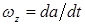, получим

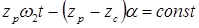. (6.5)

При 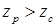гармоника вращается согласно с ротором, при 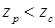– встречно ротору.

В общем случае индукторные двигатели имеют две обмотки: обмотку возбуждения и рабочую обмотку. Различают двигатели с осевым и радиальным возбуждением.

Осевое возбуждение (рис. 6.5). Тороидальная обмотка возбуждения (роль обмотки могут выполнять постоянные магниты) питается постоянным током; ее намагничивающая сила 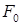создает в зазоре униполярное магнитное поле, индукция которого

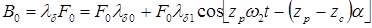(6.6)

Видно, что это поле содержит две составляющие: постоянную и переменную, являющуюся зубцовой гармоникой, число пар полюсов и угловая скорость вращения которой следующие:

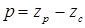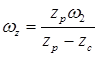; . (6.7)

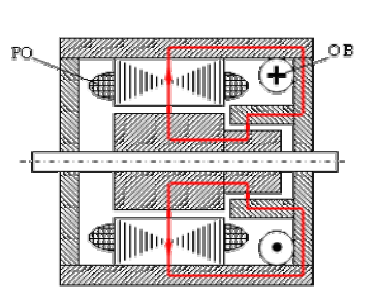
Рис.6.5. Индуктивный двигатель с осевым возбуждением

Рабочая обмотка статора (РО) питается переменным током и создает спектр гармоник намагничивающих сил, порядки и амплитуды которых зависят от схемы обмотки, ее шага, числа пазов:

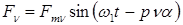, (6.8)

где 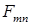– амплитуда НС n–й гармоники; 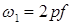– угловая частота тока;
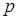– число пар полюсов.

В хорошо спроектированной машине обмоточные гармоники высоких порядков выражены слабо, поэтому будем считать, что в нашем двигателе имеет место лишь первая гармоника НС 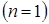. Эта НС создает свое магнитное поле. Если ограничиться первой зубцовой гармоникой проводимости (6.4) и учесть, что 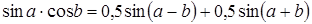, то индукция этого поля при двухсторонней зубчатости будет

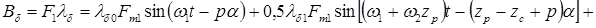
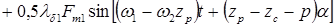. (6.9)

Поле рабочей обмотки содержит 3 составляющие: одну, обусловленную постоянной составляющей магнитной проводимости зазора, и две зубцовые гармоники, порядки и скорости вращения которых

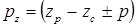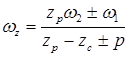; . (6.10)

Магнитные поля обеих обмоток взаимодействуют друг с другом, но только те гармоники образуют однонаправленные моменты, числа пар полюсов и скорости вращения которых одинаковые. Из сопоставления (6.7) и (6.10) получаем соотношения чисел пазов и скорость вращения индукторных двигателей с осевым возбуждением:

; .

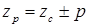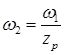Коэффициент редукции (отношение угловой скорости поля основной обмотки к угловой скорости ротора) для указанных двигателей

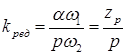. (6.12)

Радиальное возбуждение (рис. 6.6). Обе обмотки (возбуждения и рабочую) располагают на статоре. Предположим, что обмотка возбуждения имеет р пар полюсов и питается током частоты f, а рабочая обмотка имеет 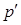пар полюсов и питается током частоты 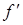. Каждая обмотка создает свой спектр гармоник магнитного поля, причем одна из них – гармоник, связанных с числом зубцов статора, а другая – с числом зубцов ротора.

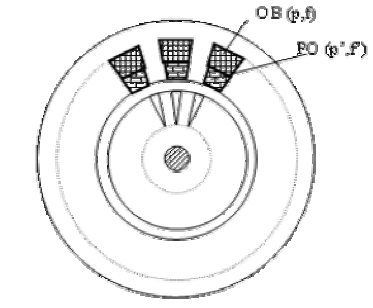
Рис. 6.6. Индукторный двигатель с радиальным возбуждением

Как и в предыдущем случае, условием создания однонаправленного момента будет равенство чисел пар полюсов и угловых скоростей вращения гармоник полей обеих обмоток. Выполнив соответствующие действия, получим соотношения чисел пазов статора и ротора, а также частоты вращения ротора индукторных двигателей с радиальным возбуждением

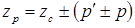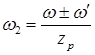; или 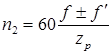. (6.13)

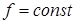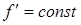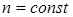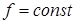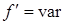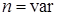Выражение частоты вращения (6.13) свидетельствует о том, что индукторные двигатели повторяют известные двигатели переменного тока, только в новом качестве – в качестве тихоходных. Действительно, если , , то , т.е. двигатель является синхронным. Если , , то , т.е. двигатель работает как асинхронный. При этом скорость вращения двигателя обратно пропорциональна не числу пар полюсов 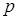, а числу пазов ротора 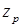, которое может быть во много раз большим 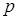, что позволяет существенно понизить скорость вращения машины. В таблице 1 приведены основные типы индукторных двигателей.

Таблица 1

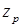
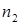
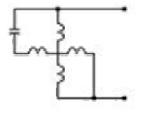
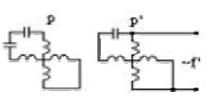
Тип двигателя	Число зубцов ротора	Скорость ротора	Коэффициент редукции	Схема обмоток
Синхронный реактивный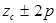
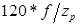
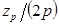
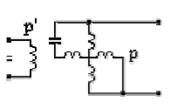
Синхронный с осевым возбуждением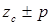
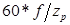
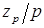
Синхронный с радиальным возбуждением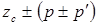

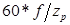
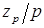
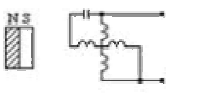
Продолжение таблицы 1

Тип двигателя	Число зубцов ротора	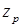Скорость ротора	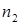Коэффициент редукции	Схема обмоток
Синхронный двойного питания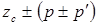
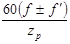
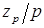
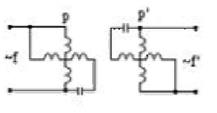
Асинхронный

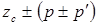
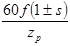
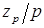
К недостаткам индукторных двигателей следует отнести сравнительно низкие энергетические показатели, что объясняется малой величиной энергии зубцовых гармоник поля.