Контрольная работа №3. Применение операционных усилителей.
Контрольная работа предполагает анализ электронных схем на основе идеальных операционных усилителей, работающих в линейном и нелинейном режимах.
Задание 1. Получить выражение, определяющее временную зависимость выходного напряжения пропорционально-интегрирующего регулятора (ПИ-регулятора) при нулевых начальных условиях.
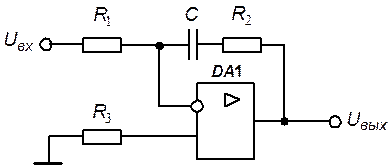
Решение. Используя законы электрического равновесия (закон Кирхгофа для токов, закон Кирхгофа для напряжений) и компонентные соотношения для резистивных и емкостных элементов, по схеме рис. 5.5 составим систему уравнений, описывающих электрические процессы в ПИ-регуляторе.
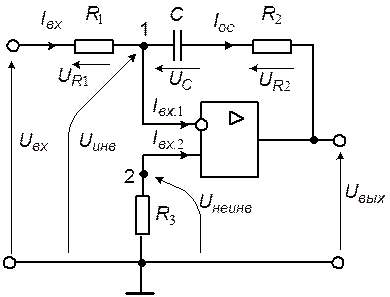
Рис. 5.5. Эквивалентная схема ПИ-регулятора
Уравнение, выражающее закон Кирхгофа для токов узла №1:
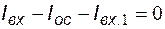 .
.
Уравнение, выражающее закон Кирхгофа для напряжений 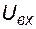 ,
, 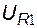 ,
, 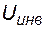 :
:
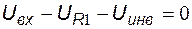 .
.
Уравнение, выражающее закон Кирхгофа для напряжений 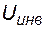 ,
, 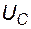 ,
, 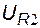 ,
, 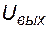 :
:
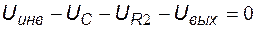 .
.
Компонентные соотношения для резистивных элементов схемы:
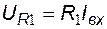 ,
, 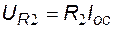 ,
, 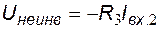 .
.
Компонентное соотношение для емкостного элемента схемы:
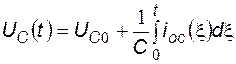 ,
,
где 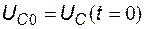 - начальное напряжение на конденсаторе.
- начальное напряжение на конденсаторе.
Подставляя компонентные соотношения в уравнения законов Кирхгофа, получаем систему уравнений вида
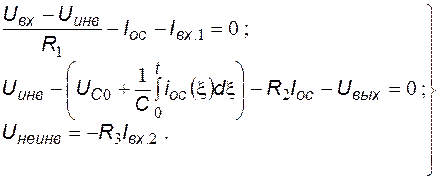
Для микросхемы идеального операционного усилителя справедливы соотношения:
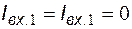 ,
, 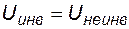 .
.
Из указанных соотношений следует, что 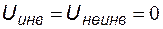 , а система уравнений принимает вид:
, а система уравнений принимает вид:
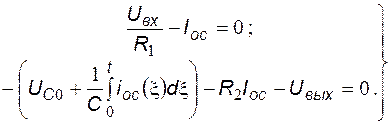
Из первого уравнения преобразованной системы выражаем ток 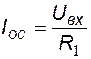 и подставляем его во второе уравнение, после чего находим выходное напряжение ПИ-регулятора:
и подставляем его во второе уравнение, после чего находим выходное напряжение ПИ-регулятора:
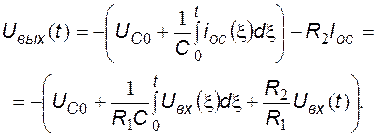
При нулевом начальном напряжении на конденсаторе ПИ-регулятора (нулевых начальных условиях) выражение для временной зависимости выходного напряжения принимает вид:
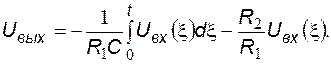
Задание 2. Определить выходное напряжение измерительного усилителя.
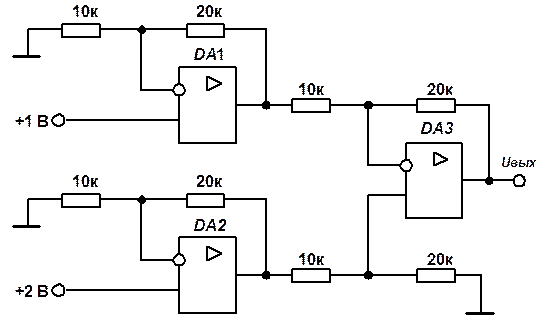
Решение. Рассматриваемый измерительный усилитель содержит три каскада, два из которых представляют собой неинвертирующие усилители постоянного тока (УПТ), а третий – дифференциальный усилитель (ДУ) (рис. 5.6).
При условии идеальных микросхем операционных усилителей DA1, DA2 выходные напряжения неинвертирующих УПТ определяются по формулам:
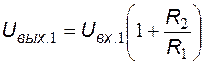 ,
, 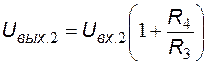 .
.
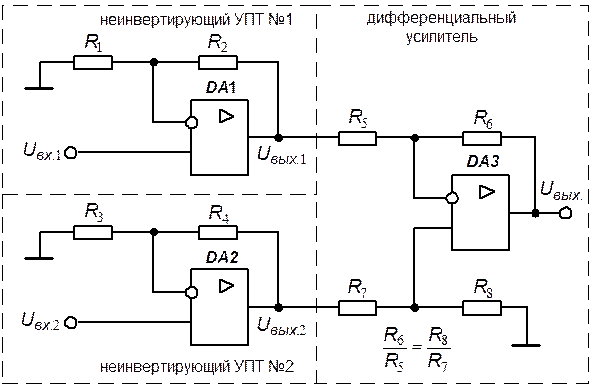
Рис. 5.6. Эквивалентная схема измерительного усилителя
Выходным напряжением измерительного усилителя является выходное напряжение ДУ. При условии идеальных микросхем операционных усилителей DA1, DA2, DA3 выходное напряжение ДУ определяется выражением:
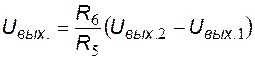 .
.
Таким образом, выходное напряжение измерительного усилителя:
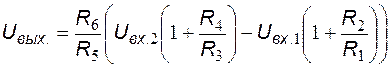 .
.
Подставляя численные значения параметров, находим
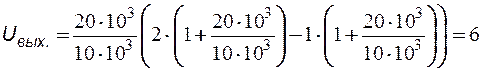 В
В
Задание 3. Определить значения выходного напряжения схемы для случаев включенного и выключенного состояний транзистора при 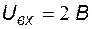 ,
, 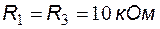 ,
, 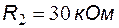 .
.
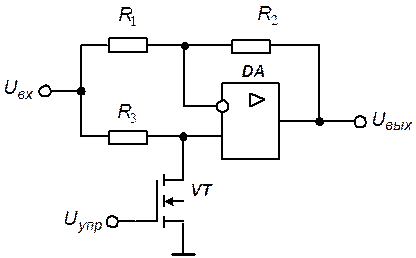
Решение. Входящие в состав схемы операционный усилитель и полевой транзистор будем считать идеальными. Сопротивление идеального полевого транзистора во включенном состоянии равно нулю, а выключенном – бесконечности.
Для случая, соответствующего включенному состоянию транзистора, справедлива схема замещения, приведенная на рис. 5.7.
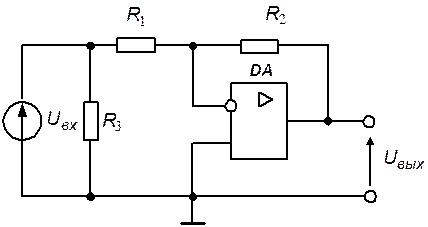
Рис. 5.7. Эквивалентная схема усилителя постоянного тока
Схема замещения соответствует инвертирующему УПТ на ОУ. Резистор 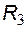 оказывается включенным параллельно идеальному источнику э.д.с. и не влияет на потенциал входного узла схемы. Выходное напряжение определяется соотношением
оказывается включенным параллельно идеальному источнику э.д.с. и не влияет на потенциал входного узла схемы. Выходное напряжение определяется соотношением
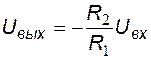 .
.
Подставляя числовые значения, находим
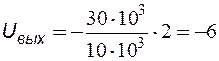 В.
В.
Для случая, соответствующего включенному состоянию транзистора, справедлива схема замещения, представленная на рис. 5.8.
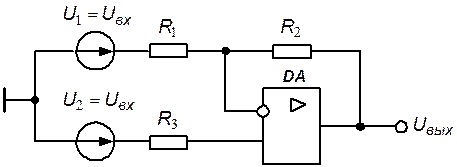
Рис. 5.8. Схема замещения усилителя постоянного тока
Если операционный усилитель охвачен цепью отрицательной обратной связи и выходное напряжение не превышает напряжения насыщения, то операционный усилитель работает в линейном режиме. В этом случае к расчету схемы применим принцип суперпозиции, а выходное напряжение определяется выражением
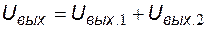 ,
,
где 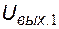 - составляющая выходного напряжения, обусловленная действием э.д.с.
- составляющая выходного напряжения, обусловленная действием э.д.с. 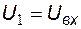 при
при 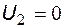 ;
; 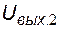 - составляющая выходного напряжения, обусловленная действием э.д.с.
- составляющая выходного напряжения, обусловленная действием э.д.с. 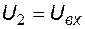 при
при 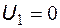 .
.
При 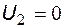 схема эквивалентна инвертирующему УПТ на ОУ, поэтому
схема эквивалентна инвертирующему УПТ на ОУ, поэтому
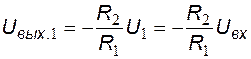 .
.
При 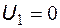 схема эквивалентна неинвертирующему УПТ на ОУ, поэтому
схема эквивалентна неинвертирующему УПТ на ОУ, поэтому
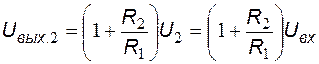 .
.
В итоге получаем выражение выходного напряжения в виде
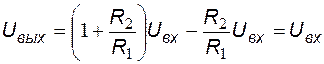 .
.
Выражение для выходного напряжения схемы показывает, что в случае разомкнутого ключа схема является схемотехнической разновидностью повторителя напряжения.
Подставляя числовые данные, находим 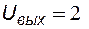 В.
В.
Задание 4. Получить выражение, определяющее коэффициент передачи напряжения активного полосового RC-фильтра.
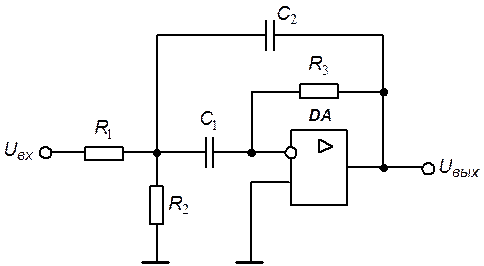
Решение. Входящий в состав схемы операционный усилитель будем считать идеальным.
На рис. 5.9 представлена операторная схема замещения активного полосового RC-фильтра, в которой в качестве параметров пассивных компонентов указаны операторные проводимости: 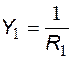 ,
, 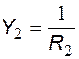 ,
, 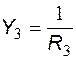 ,
, 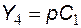 ,
, 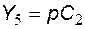 .
.
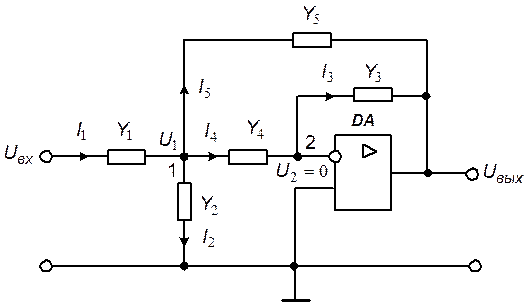
Рис. 5.9. Схема замещения полосового фильтра
Для операторной схемы замещения составим систему уравнений, используя метод узловых потенциалов:
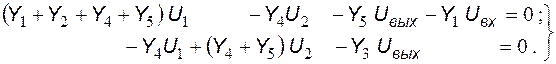
Поскольку операционный усилитель охвачен цепью отрицательной обратной связи, то он будет работать в линейном режиме, пока выходное напряжение не превысит напряжения насыщения. В этом случае входное дифференциальное напряжение идеального операционного усилителя равно нулю, следствием чего является равенство потенциалов на неинвертирующем и инвертирующем входах ОУ. В рассматриваемой схеме неинвертирующий вход операционного усилителя заземлен, то есть его потенциал, а значит и потенциал инвертирующего входа (узла 2), равны нулю ( 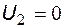 ).
).
В результате система уравнений приобретает вид:
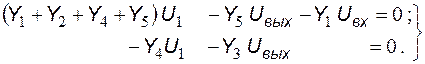
Из второго уравнения системы выразим потенциал узла 1 через потенциал на выходе схемы:
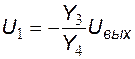 .
.
Подставив полученное соотношение в первое уравнение системы и выполнив необходимые преобразования, выразим выходной потенциал через входной:
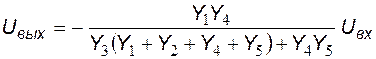 .
.
Из последнего выражения найдем коэффициент передачи напряжения активного полосового RC-фильтра:
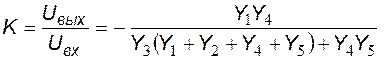 .
.
Представим выражение для коэффициента передачи напряжения в операторной дробно-рациональной форме:
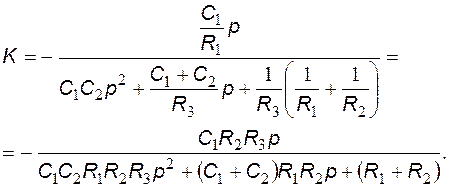
Приведем выражение коэффициента передачи напряжения к канонической форме 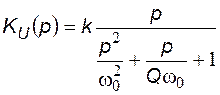 , где Q – добротность, а
, где Q – добротность, а 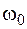 - резонансная круговая частота полосового фильтра:
- резонансная круговая частота полосового фильтра:
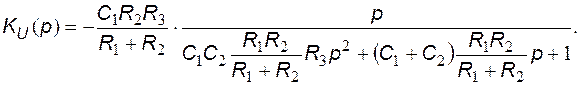 Из последнего выражения следует, что резонансная круговая частота и добротность связаны с параметрами пассивных компонентов рассматриваемого полосового активного RC-фильтра соотношениями
Из последнего выражения следует, что резонансная круговая частота и добротность связаны с параметрами пассивных компонентов рассматриваемого полосового активного RC-фильтра соотношениями
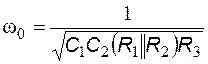 ,
, 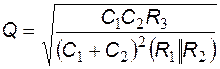 .
.
Задание 5. Построить временную диаграмму выходного напряжения предварительно обнуленного интегратора для заданной временной диаграммы напряжения на входе при 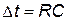 .
.
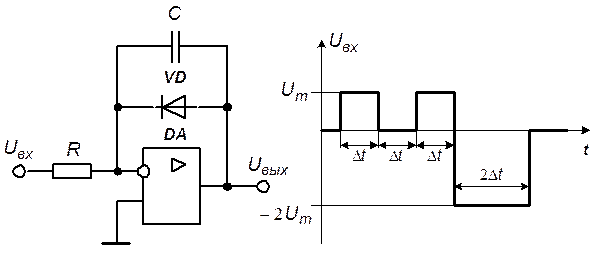
Решение. Входящие в состав схемы операционный усилитель и диод будем считать идеальными.
Сопротивление идеального диода при прямом смещении равно нулю, а при обратном смещении – бесконечности. В зависимости от состояния диода реализуются два режима работы схемы.
При обратном смещении диода справедлива схема замещения, показанная на рис. 5.10.
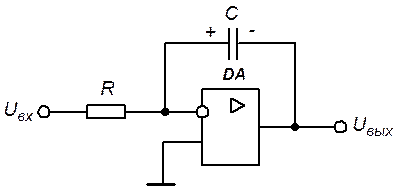
Рис. 5.10. Схема замещения интегратора
Схема замещения соответствует инвертирующему интегратору на ОУ, для которого связь выходного напряжения со входным во временной форме определяется выражением:
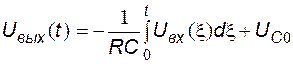 ,
,
где 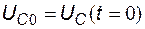 - начальное напряжение на конденсаторе.
- начальное напряжение на конденсаторе.
При прямом смещении диода, справедлива схема замещения, приведенная на рис. 5.11.
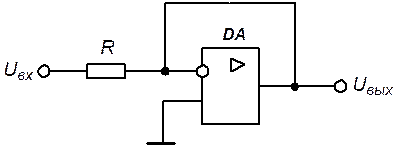
Рис. 5.11. Схема замещения интегратора
Схема замещения соответствует инвертирующему УПТ с нулевым сопротивлением отрицательной обратной связи, при этом выходное напряжение определяется соотношением:
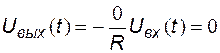 .
.
Построение временной диаграммы выходного напряжения будем проводить, последовательно рассматривая интервалы, на каждом из которых и состояние диода и значение входного напряжения остаются неизменными (рис. 5.12). Для получения более компактных выражений выходного напряжения и упрощения графического построения временной диаграммы отсчет времени будем вести от начала соответствующего интервала.
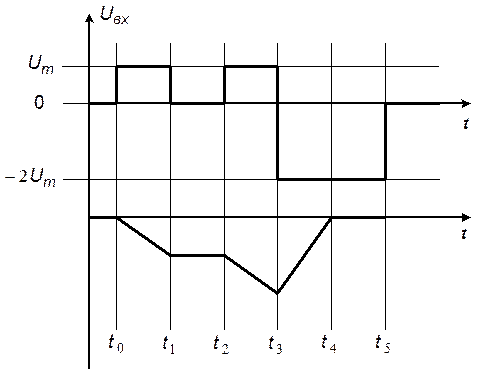
Рис. 5.12. Временные диаграммы входного и выходного напряжений интегратора
На интервале 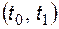 из-за инвертирующего включения операционного усилителя выходное напряжение отрицательное, диод закрыт и схема работает как интегратор (рис. 5.10). Начальное напряжение на конденсаторе равно
из-за инвертирующего включения операционного усилителя выходное напряжение отрицательное, диод закрыт и схема работает как интегратор (рис. 5.10). Начальное напряжение на конденсаторе равно 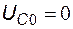 . Выходное напряжение определяется выражением:
. Выходное напряжение определяется выражением:
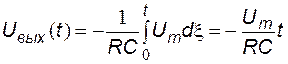 .
.
В конце интервала 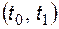 выходное напряжение становится равным
выходное напряжение становится равным 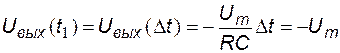 .
.
На интервале 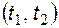 полярность напряжения на конденсаторе не изменяется, диод закрыт и схема работает как интегратор (рис. 5.10). Начальное напряжение на конденсаторе равно
полярность напряжения на конденсаторе не изменяется, диод закрыт и схема работает как интегратор (рис. 5.10). Начальное напряжение на конденсаторе равно 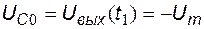 . Выходное напряжение определяется выражением:
. Выходное напряжение определяется выражением:
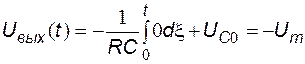 .
.
На интервале 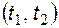 выходное напряжение остается постоянным, что соответствует работе интегратора в режиме хранения.
выходное напряжение остается постоянным, что соответствует работе интегратора в режиме хранения.
В конце интервала 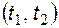 выходное напряжение равно
выходное напряжение равно 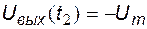 .
.
На интервале 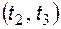 полярность напряжения на конденсаторе не изменяется, диод закрыт и схема работает как интегратор (рис. 5.10). Начальное напряжение на конденсаторе равно
полярность напряжения на конденсаторе не изменяется, диод закрыт и схема работает как интегратор (рис. 5.10). Начальное напряжение на конденсаторе равно 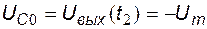 . Выходное напряжение определяется выражением:
. Выходное напряжение определяется выражением:
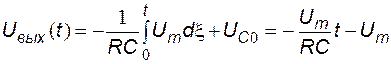 .
.
В конце интервала 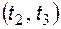 выходное напряжение становится равным
выходное напряжение становится равным 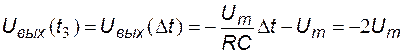 .
.
На интервале 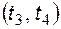 полярность напряжения на конденсаторе не изменяется, диод закрыт и схема работает как интегратор (рис. 5.10). Начальное напряжение на конденсаторе равно
полярность напряжения на конденсаторе не изменяется, диод закрыт и схема работает как интегратор (рис. 5.10). Начальное напряжение на конденсаторе равно 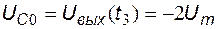 . Выходное напряжение определяется выражением:
. Выходное напряжение определяется выражением:
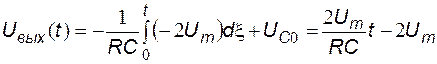 .
.
В конце интервала 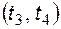 выходное напряжение становится равным
выходное напряжение становится равным 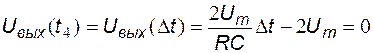 .
.
В момент времени 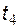 напряжение на конденсаторе стремится изменить полярность, что вызывает включение диода и изменение структуры схемы (рис. 5.11). На интервале
напряжение на конденсаторе стремится изменить полярность, что вызывает включение диода и изменение структуры схемы (рис. 5.11). На интервале 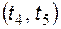 выходное напряжение равно нулю.
выходное напряжение равно нулю.
Задание 6. Построить временную диаграмму выходного напряжения схемы по заданной временной диаграмме напряжения на входе
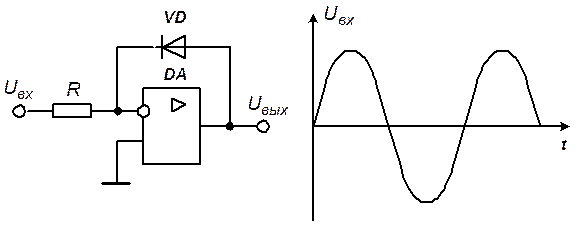
Решение. Входящие в состав схемы операционный усилитель и диод будем считать идеальными. Сопротивление идеального диода при прямом смещении равно нулю, а при обратном смещении – бесконечности.
Передаточная характеристика идеального операционного усилителя представлена на рис. 5.13
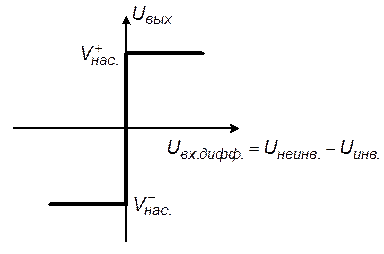
Рис. 5.13. Передаточная характеристика идеального операционного усилителя
При положительной полуволне входного напряжения диод закрыт и схема приобретает вид рис. 5.14,а. Так как отрицательная обратная связь в схеме отсутствует, то автоматического выравнивания потенциалов инвертирующего и неинвертирующего входов ОУ не происходит. Напряжения на неинвертирующем и инвертирующем входах операционного усилителя, а также его входное дифференциальное напряжения определяются выражениями:
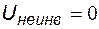 ,
, 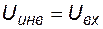 ,
, 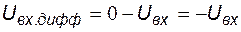 .
.
Для положительной полуволны напряжения 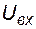 входное дифференциальное напряжение ОУ является отрицательным. Из передаточной характеристики следует, что выходное напряжение в этом случае равно отрицательному напряжению насыщения
входное дифференциальное напряжение ОУ является отрицательным. Из передаточной характеристики следует, что выходное напряжение в этом случае равно отрицательному напряжению насыщения 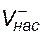 .
.
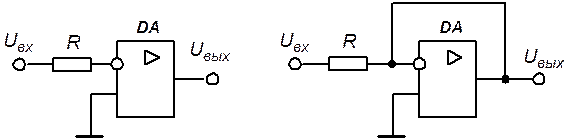 а б
а б
Рис. 5.14. Схемы замещения ограничителя напряжения
При отрицательной полуволне входного напряжения диод открыт и схема соответствует инвертирующему УПТ с нулевым сопротивлением отрицательной обратной связи (рис. 5.14,б), при этом выходное напряжение определяется соотношением:
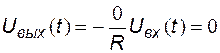 .
.

Рис. 5.15. Временные диаграммы входного и выходного напряжений ограничителя напряжения
Задание 7. Получить выражение выходного напряжения для прецизионной схемы восстановления постоянной составляющей, если 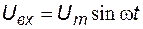 ;
; 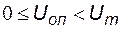 .
.
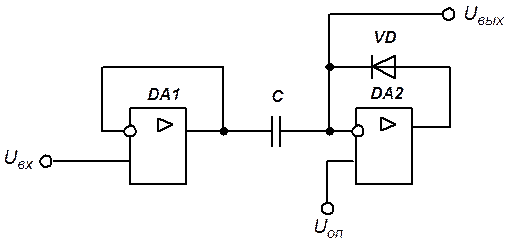
Решение. Эквивалентная расчетная схема представлена на рис. 5.16. Входящие в состав схемы операционные усилители и диод будем считать идеальными.
Операционный усилитель DA1 включен по схеме повторителя напряжения, поэтому справедливо соотношение 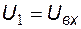 .
.
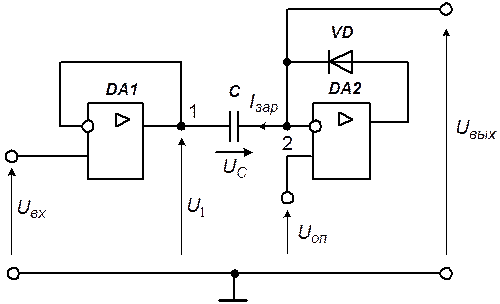
Рис. 5.16. Эквивалентная схема фиксатора уровня
Выходное напряжение схемы 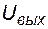 определяется выражением, полученным применением закона Кирхгофа для напряжений
определяется выражением, полученным применением закона Кирхгофа для напряжений 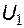 ,
, 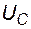 ,
, 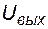 :
:
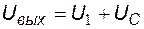 .
.
Ток через конденсатор 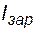 может протекать только при включенном состоянии диода в направлении, указанном на рис. 5.16. Когда диод включен, операционный усилитель DA2 работает в режиме повторителя, обеспечивая равенство
может протекать только при включенном состоянии диода в направлении, указанном на рис. 5.16. Когда диод включен, операционный усилитель DA2 работает в режиме повторителя, обеспечивая равенство 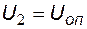 . Ток
. Ток 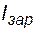 обеспечит заряд конденсатора до напряжения, равного максимальной разности напряжений
обеспечит заряд конденсатора до напряжения, равного максимальной разности напряжений 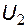 и
и 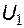 :
: 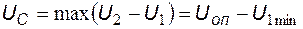 . Для заданного синусоидального входного напряжения
. Для заданного синусоидального входного напряжения 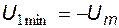 , следовательно,
, следовательно, 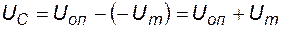 .
.
Таким образом, выражение для выходного напряжения принимает вид
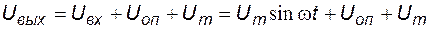 .
.
Задание 8. Определить выходное напряжение измерительной схемы при 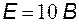 ,
, 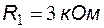 ,
, 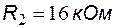 ,
, 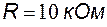 ,
, 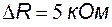 .
.
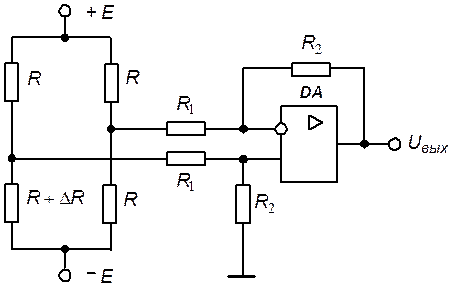
Решение. Измерительная схема построена на основе применения измерительного моста (рис. 5.17), на выходе которого включен дифференциальный усилитель на ОУ.
Представим измерительный мост эквивалентными генераторами напряжения относительно узлов 1 и 0, 2 и 0.
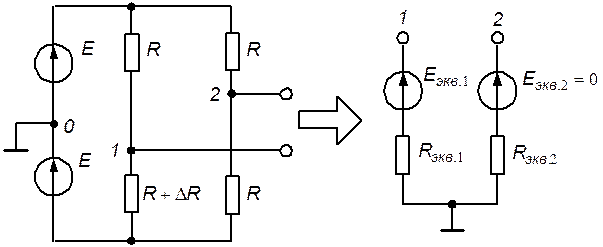
Рис. 5.17. Эквивалентная схема измерительного моста
ЭДС и внутренние сопротивления эквивалентных генераторов напряжения определяются соотношениями:
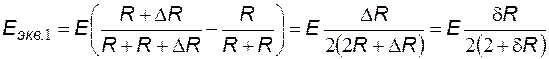 ,
,
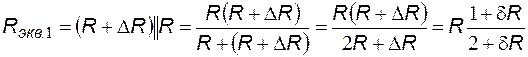 ,
,
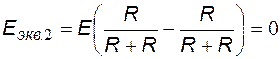 ,
, 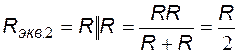 ,
,
где 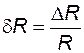 - относительное приращение сопротивления
- относительное приращение сопротивления 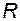 .
.
Замена измерительного моста эквивалентными генераторами напряжения приводит к схеме замещения рис. 5.18.
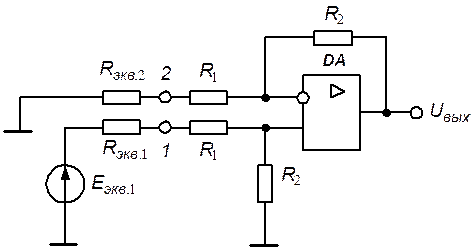
Рис. 5.18. Эквивалентная схема измерительного усилителя
Схема замещения соответствует неинвертирующему УПТ на ОУ, для которого выходное напряжение определяется выражением 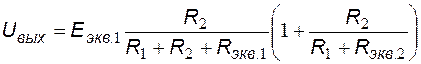 .
.
Преобразуем полученную формулу с учетом выражений параметров эквивалентных генераторов напряжения 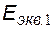 ,
, 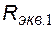 ,
, 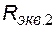 :
:
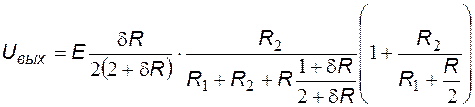 .
.
Подставляя числовые значения параметров, находим:
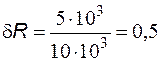 ;
;
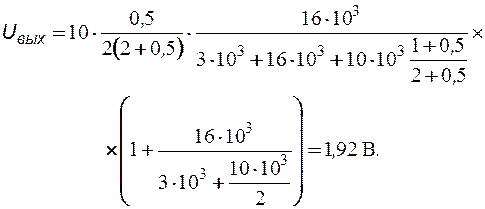
Задание 9. Получить выражение выходного напряжения активного выпрямителя среднего значения напряжения.
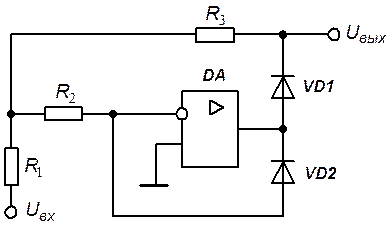
Решение. Входящие в состав схемы операционный усилитель и диоды будем считать идеальными.
При положительной полярности входного напряжения диод VD1 находится в выключенном, а диод VD2 во включенном состояниях. В этом случае структуре выпрямителя соответствует схема замещения рис. 5.19, а.

а б
Рис. 5.19. Схемы замещения прецизионного выпрямителя
Так как операционный усилитель охвачен отрицательной обратной связью, происходит автоматическое выравнивание потенциалов его инвертирующего и неинвертирующего входов, причем справедливы равенства 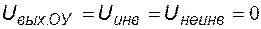 . Потенциал в точке 1 схемы замещения определяется входным напряжением и коэффициентом передачи резистивного делителя
. Потенциал в точке 1 схемы замещения определяется входным напряжением и коэффициентом передачи резистивного делителя 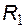 -
- 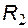 в соответствии с формулой:
в соответствии с формулой:
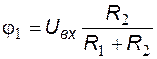 .
.
Выражение выходного напряжения выпрямителя находим на основе второго закона Киррхгофа:
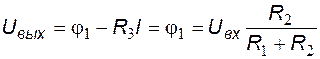 .
.
При отрицательной полярности входного напряжения диод VD1 находится во включенном, диод VD2 – в выключенном состояниях, а схема замещения выпрямителя принимает вид рис. 5.4.15,б. Схема замещения выпрямителя соответствует инвертирующему УПТ на ОУ, поэтому связь выходного и входного напряжений выражается формулой
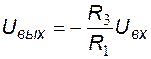 .
.
Таким образом, выходное напряжение выпрямителя среднего значения напряжения определяется выражением
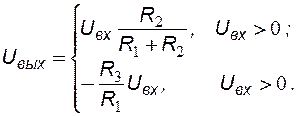
Дата добавления: 2022-02-05; просмотров: 415;











