Решение оптимизационных задач
Существует множество задач, которые трудно решить вручную. Формулировка таких задач может представлять собой систему уравнений с несколькими неизвестными и набор ограничений на решение. В частности, к таким задачам относятся классические задачи линейного программирования:
- Ассортимент продукции. Максимизация выпуска товаров при ограничениях на сырье для производства этих товаров;
- Штатное расписание. Составление штатного расписания для достижения наилучших результатов при наименьших расходах;
- Планирование перевозок. Минимизация затрат на транспортировку товаров;
- Составление смеси. Достижение заданного качества смеси при наименьших расходах;
- Портфель ценных бумаг. Обеспечение максимального дохода при минимальном риске и многие другие.
Средство Поиск решения (меню Сервис)позволяет находить значения в целевой ячейке, изменяя при этом до 200 переменных, удовлетворяющих заданным критериям.
1. Задачи, которые лучше всего решаются данным средством, имеют три аспекта:
2. Единственная цель, например, максимизация прибыли или минимизация расходов.
3. Ограничения, выражающиеся, как правило, в виде неравенств, например, объем используемого сырья не может превышать объем сырья, имеющегося на складе.
4. Набор входных значений, непосредственно или косвенно влияющих на ограничения и на оптимизируемые величины.
Решение задачи следует начинать с организации рабочего листа в соответствии с пригодной для Поиска решения моделью. Для этого надо хорошо понимать взаимосвязи между переменными и формулами, т.е. четко представлять постановку задачи.
Исходные данные для запуска средства Поиск решения должны быть представлены в виде таблицы, которая содержит формулы, отражающие зависимости между значениями таблицы.
Затем в меню СЕРВИС выбратькоманду Поиск решения ив полеУстановить Целевую Ячейку указать ячейку с целевой функцией. Тип связи между целевой ячейкой и решением задается путем выбора переключателя(максимизировать, минимизировать или сделать равным определенному значению). В поле Изменяя Ячейки указать ячейки, которые могут быть изменены в процессе Поиска Решения для достижения нужного результата.
После установки всех параметров нажать кнопку «Выполнить».
На рис. 3 приведен вид окна «Поиск решения»
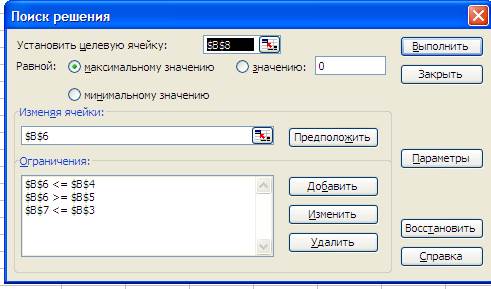
Рис. 3 - Вид окна Поиск решения
Лабораторная работа 3. Освоение технологии поиска решения.
Содержание задания:Для производства четырех типов изделий С1, С2, С3, С4 предприятие должно использовать три вида сырья В1, В2, В3, запасы которого на планируемый период составляют соответственно 1000, 600, 150.
В приведенной ниже таблице даны нормы расхода каждого вида сырья на производство единицы изделия, прибыль от реализации единицы изделия и запасы сырья по видам.
Таблица 5 – Исходные данные
| А | B | C | D | E | F | |
| Виды | Запасы | Нормы расхода на изделия | ||||
| Сырья | сырья | С1 | С2 | С3 | С4 | |
| В1 | ||||||
| В2 | ||||||
| В3 | ||||||
| Прибыль от реализации | 2,5 |
Требуется составить такой план выпуска указанных изделий, чтобы обеспечить максимальную прибыль от реализации.
Математическая постановка задачи.
Обозначим через Х1, Х2, Х3 и Х4 количество единиц соответствующих изделиям С1, С2, С3 и С4. Математическая модель задачи будет иметь следующий вид:
найти максимум функции
У=6 Х1 + 2Х2 + 2,5Х3 + 4Х4
при выполнении ограничений
5Х1 + Х2 + 2 Х4 <= 1000
4Х1 + 2Х2 + 2Х3 + Х4 <= 600
Х1 + 2Х3 + Х4 <= 150
Х1 >= 0, Х2 >= 0, Х3 >= 0, Х4 >= 0,
Организация данных на рабочем листе:
1. В ячейках А1: F6 – разместите исходную таблицу.
2. Ячейки А11,…,А14 зарезервируйте за переменными Х1,…,Х4 соответственно.
3. В ячейку А15 введите целевую функцию
= 6 * А11 + 2 * А12 + 2,5 * А13 + 4 * А14
4. В ячейки А16 – А18 введите ограничения:
= 5 * А11 + А12 +2 * А14
= 4 * А11 + 2 * А12 + 2 * А13 + А14
= А11 + 2 * А13 + А14
Дата добавления: 2021-12-14; просмотров: 370;











