Расчет прочности контактного шва в сжатой зоне

Расчет прочности контактного шва между дополнительными бетоном (арматурой) сжатой зоны и усиливаемой конструкцией производится из условия

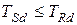. (9.13)

Сдвигающее усилие в шве от внешней нагрузки со стороны свободной опоры определяется из условия равновесия сил в нормальном сечении (рис. 9.10):

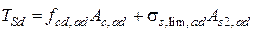, (9.14)

где 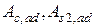– соответственно площадь поперечного сечения сжатой зоны бетона и сжатой арматуры наращивания.

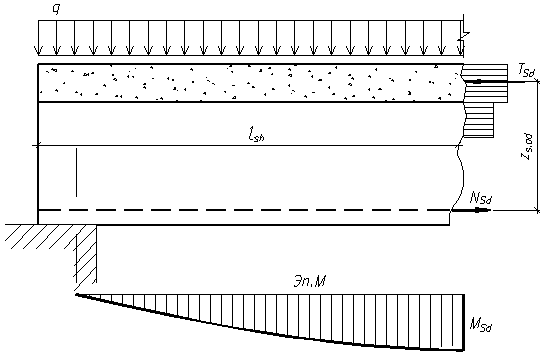
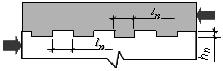
Рис. 9.10. Схема для определения усилий и расчетной длины контактного шва

Длина поверхности сдвига 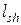принимается равной расстоянию от торца усиливаемой конструкции до рассматриваемого нормального сечения. Для сжатых конструкций, усиленных железобетонной обоймой или рубашкой с передачей нагрузки только на усиливаемую конструкцию (например, местная обойма), длина поверхности сдвига определяется расстоянием от начала поврежденного участка до конца обоймы.

Предельное сдвигающее усилие, воспринимаемое контактным швом, определяется по формуле

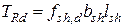, (9.15)

где 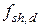– среднее по длине участка суммарное расчетное сопротивление сдвигу контактного шва; 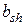– расчетная ширина поверхности сдвига.

В общем случае среднее суммарное расчетное сопротивление сдвигу контактного шва принимается равным

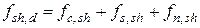, (9.16)

где 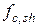– сопротивление шва сдвигу за счет сцепления, механического зацепления и обжатия бетона; 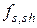– сопротивление шва сдвигу за счет работы на срез дополнительной поперечной арматуры, пересекающей шов; 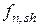– сопротивление шва сдвигу за счет работы поперечных шпонок.

При учете в расчетах работы поперечных шпонок сопротивление шва сдвигу 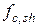не учитывается.

При учете совместной работы шпонок и дополнительной поперечной арматуры расчетное сопротивление контактного шва сдвигу принимается равным

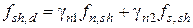, (9.17)

где 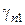, 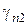– коэффициенты, равные:

- ;

- .

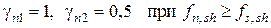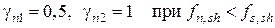Сопротивление контактного шва сдвигу 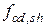определяется по формуле

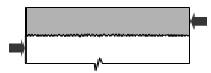
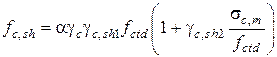, (9.18)

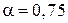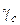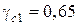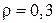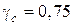где – коэффициент, учитывающий длительность действия нагрузки; – коэффициент, учитывающий влияние многократно повторяющейся нагрузки, равен: при коэффициенте асимметрии цикла нагружений и при 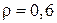, (применение плоского гладкого неармированного контакта при действии многократно повторяющейся нагрузки не допускается); 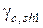– коэффициент, учитывающий влияние состояния поверхности контактного шва, принимается в интервале 0,3…0,8; 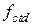– расчетное сопротивление бетона более низкого класса из сопрягаемых; 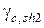– коэффициент, учитывающий влияние состояния поверхности контактного шва при его обжатии, принимается в интервале 0,8…2,2; 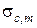– среднее напряжение обжатия контактного шва

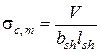. (9.19)

При расчете прочности контактных швов у неразрезных опор принимается .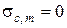

Сопротивление шва сдвигу 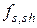за счет работы поперечной арматуры определяется по формуле

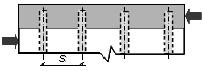
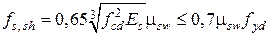, (9.20)

где 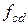– расчетное сопротивление бетона усиления сжатию; 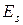– модуль упругости поперечной арматуры; 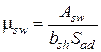– коэффициент поперечного армирования; 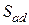– шаг дополнительных поперечных стержней.

Сопротивление шва сдвигу за счет работы поперечных бетонных шпонок определяется как меньшее значение из условий среза и смятия:

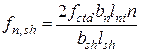, (9.21)

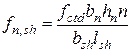, (9.22)

где 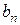, , 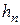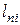– ширина, высота и длина шпонок; 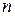– число шпонок на расчетной поверхности сдвига.

Расчетная ширина 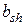принимается равной ширине контакта в месте сопряжения усиливаемой конструкции и бетона наращивания. Для сжатых конструкций, усиленных обоймой или рубашкой с передачей нагрузки только на конструкцию, 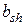принимается равной сумме сторон поперечного сечения усиливаемой конструкции, сопряженных с бетоном усиления.

Вопросы для самоконтроля

1. Каким образом, в общем случае, производится усиление сжатой зоны эксплуатируемых железобетонных конструкций?

2. Как обеспечивается совместная работа дополнительного бетона и арматуры с усиливаемой конструкцией при усилении ее сжатой зоны?

3. Какими методами производится увеличение поперечного сечения сжатой зоны железобетонных конструкций?

4. Назовите конструктивные требования при увеличении поперечного сечения сжатой зоны железобетонных конструкций путем наращивания, рубашек или обойм.

5. Какие конструктивные требования необходимо выполнять при усилении поврежденного участка сжатой железобетонной конструкции местной железобетонной обоймой?

6. Приведите примеры усиления со стороны сжатой зоны железобетонных панелей перекрытия.

7. В каких случаях и как производится усиление сжатых железобетонных конструкций путем ограничения поперечных деформаций?

8. Изложите алгоритм расчета прочности по нормальному сечению усиленных в сжатой зоне изгибаемых железобетонных элементов.

9. Как производится проверка прочности усиленных центрально-сжатых железобетонных элементов?

10. В чем заключается особенность поверочного расчета прочности по нормальному сечению железобетонных элементов, усиленных спиральной или кольцевой арматурой?

11. Как производится проверка прочности контактного шва при усилении сжатой зоны эксплуатируемых железобетонных конструкций?

Тема 10. ОСОБЕННОСТИ РАСЧЕТА ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ, УСИЛЕННЫХ УВЕЛИЧЕНИЕМ ПОПЕРЕЧНОГО СЕЧЕНИЯ, НА ОСНОВЕ ДЕФОРМАЦИОННОЙ МОДЕЛИ

Общие положения

Расчет прочности и параметров напряженно-деформированного состояния на любом этапе деформирования железобетонных элементов, усиленных увеличением поперечного сечения с обеспечением совместной работы дополнительного бетона и арматуры с усиливаемым элементом по всей длине контакта, производится на основе деформационной модели. Деформационная модель расчета позволяет в полной мере учитывать особенность работы усиленных под нагрузкой железобетонных элементов, которые после усиления превращаются в многокомпонентную конструкцию, состоящую из основной части, находящейся в определенном напряженно-деформированном состоянии, и дополнительной части – в первоначальном состоянии.

Для расчета усиленных железобетонных элементов принимаются те же гипотезы, что и при выполнении поверочных расчетов эксплуатируемых железобетонных конструкций (см. тему 4). Аналогично сечению основной части элемента, поперечное сечение дополнительной части разбивается на элементарные площадки или при плоской задаче – на элементарные слои. Гипотеза плоских сечений для относительных деформаций всего сечения усиленного под нагрузкой железобетонного элемента, состоящего из основной и дополнительной части, не выполняется, поскольку при усилении в основной части сечения уже имеются относительные деформации от воздействия нагрузки. Учитывая совместную работу основной и дополнительной частей сечения после усиления, принимается гипотеза плоских сечений отдельно для относительных деформаций дополнительной части и для приращений относительных деформаций основной части конструкции после усиления. Тогда относительные деформации элементарного слоя основной части сечения элемента представляются как сумма относительных деформаций до усиления и относительных деформаций после усиления.

При этом параметры диаграмм состояния бетона и арматуры усиливаемой конструкции определяются по проектным данным или результатам испытаний, а дополнительного бетона и арматуры – по СНБ 5.03.01-02.

10.2. Расчет прочности усиленных элементов по сечению,
нормальному к продольной оси

Расчет прочности железобетонных элементов, усиленных увеличением поперечного сечения в растянутой и сжатой зонах, под нагрузкой производится в два этапа. На первом этапе вычисляют относительные деформации элементарных площадок усиливаемого элемента от действующей при усилении нагрузки, которые согласно гипотезе плоских сечений определяются кривизной 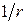, их расстоянием от центра тяжести сечения 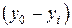и продольными относительными деформациями .

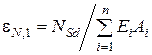На втором этапе расчет производится для усиленного сечения элемента методом последовательного нагружения с реализацией итерационного процесса вычисления относительных деформаций в элементарных площадках.

Относительные деформации в элементарных площадках сечения усиленного элемента (рис. 10.1) определяются из условий:

§ для изгибаемых элементов:

- в основном сечении

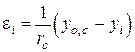; (10.1)

- в дополнительном сечении

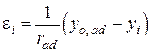; (10.2)

§ для внецентренно сжатых (растянутых) элементов:

- в основном сечении

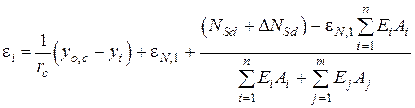; (10.3)

- в дополнительном сечении

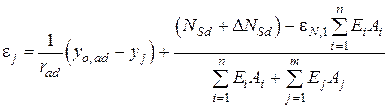. (10.4)

Рис. 10.1. Расчетное сечение (а) и распределение деформаций усиленного железобетонного элемента: б – изгибаемого; в – внецентренно сжатого

Значения 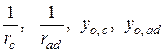определяются из совместного решения уравнений:

- для изгибаемых элементов:

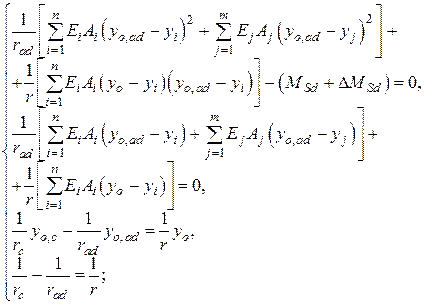
(10.5)

- для внецентренно сжатых (растянутых) элементов:

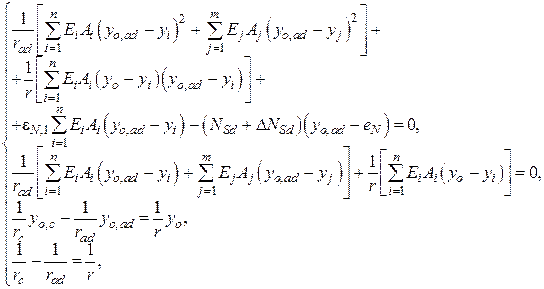
(10.6)

где 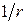– кривизна основного (усиливаемого) элемента от действующей при усилении нагрузки; 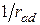– кривизна дополнительного (усиливающего) элемента от действующей нагрузки после усиления; 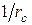– кривизна основного элемента от действующей после усиления нагрузки; 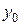– расстояние от выбранной оси до центра тяжести сечения основного элемента при усилении; 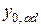– расстояние от выбранной оси до центра тяжести сечения дополнительного элемента после усиления; 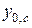– расстояние от выбранной оси до центра тяжести сечения основного элемента после усиления; 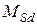, 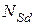– соответственно изгибающий момент и продольное усилие от действующей при усилении нагрузки (растягивающее усилие принимается со знаком «плюс», сжимающее – «минус».); 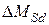, 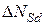– приращение соответственно изгибающего момента и продольного усилия от дополнительной нагрузки, приложенной после усиления; 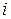, 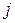– количество элементарных площадок соответственно в основном и дополнительном сечении усиленного железобетонного элемента.

На каждой ступени нагружения из первых двух уравнений систем (10.5) и (10.6) методом итераций определяются неизвестные 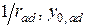. Из третьего и четвертого уравнений вычисляются 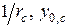. По формулам (10.1) … (10.4) определяются относительные деформации элементарных площадок основного и дополнительного сечения.

При расчете по деформационной модели железобетонных элементов, усиленных увеличением поперечного сечения, в случае косого изгиба и косого внецентренного сжатия-растяжения расчет производится относительно двух осей.

Относительные деформации в элементарных площадках сечения усиленного железобетонного элемента (рис. 10.2) определяются из условий:

§ для косоизгибаемых элементов:

- в основном сечении

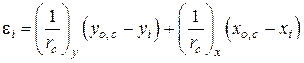; (10.7)

- в дополнительном сечении

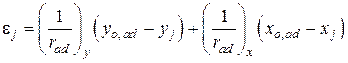; (10.8)

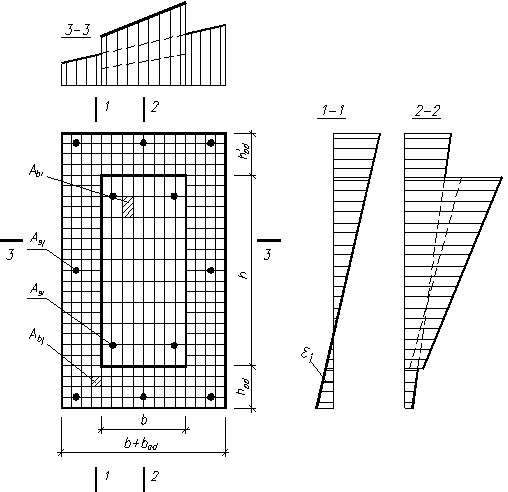
Рис. 10.2. Расчетная схема кососжатого железобетонного элемента,
усиленного обоймой

§ для кососжатых элементов:

- в основном сечении

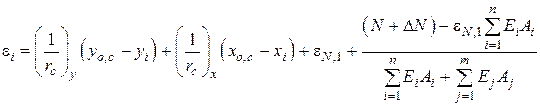; (10.9)

- в дополнительном сечении

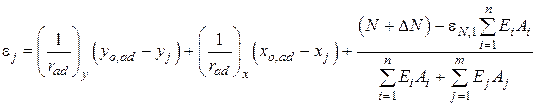. (10.10)

Значения 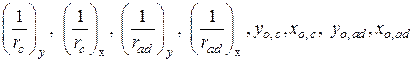определяются из совместного решения уравнений:

- для косоизгибаемых элементов

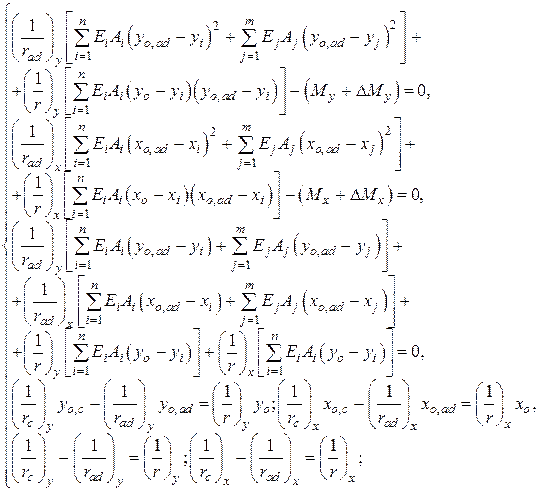
(10.11)

- для кососжатых элементов

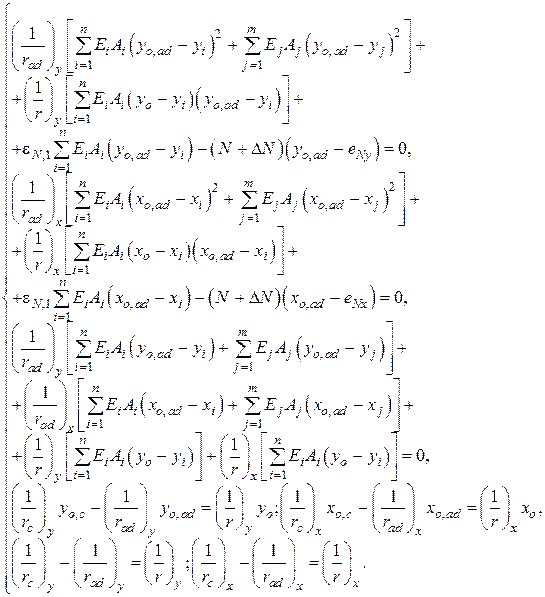
(10.12)

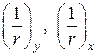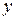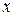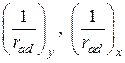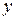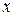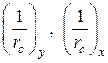где – кривизны основного элемента от действующей при усилении нагрузки соответственно в плоскости оси и ; – кривизны дополнительного элемента от нагрузки после усиления соответственно в плоскости оси и ; – кривизна основного элемента от действующей после усиления нагрузки соответственно в плоскости ос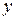и и 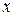; 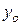, 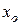– расстояния от выбранных осей до центра изгиба сечения усиливаемого элемента при усилении соответственно в плоскости оси 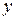и ; , – 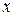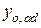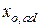расстояния от выбранных осей до центра изгиба сечения дополнительного элемента после усиления соответственно в плоскости ос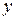и и 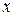; 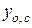, 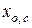– расстояния от выбранных осей до центра изгиба сечения основного элемента после усиления соответственно в плоскости ос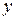и 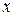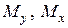и ; и 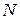– составляющие изгибающего момента соответственно в плоскости ос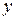и и 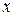и продольная сила от действующей при усилении нагрузки; 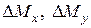и – 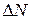составляющие приращения изгибающего момента соответственно в плоскости ос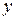и и 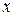и продольного усилия от дополнительной нагрузки, приложенной после усиления; 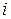, 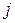– количество элементарных площадок соответственно в основном и дополнительном сечении усиленного железобетонного элемента.

Из первых трех уравнений систем (10.11) и (10.12) методом итераций определяются неизвестные 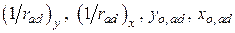. Из последних четырех уравнений вычисляются 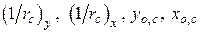. По формулам (10.7)…(10.10) определяются относительные деформации элементарных площадок основного и дополнительного сечения.

Прочность усиленного элемента устанавливается методом последовательного нагружения. Аналогично усиленным железобетонным элементам, работающим под нагрузкой в одной плоскости, максимальное усилие от внешней нагрузки, при котором относительные деформации бетона или арматуры (основного или дополнительного сечений) достигают предельных значений, соответствует прочности усиленного элемента.

Расчет прочности железобетонных элементов, усиленных увеличением поперечного сечения в растянутой и сжатой зонах при полной предварительной разгрузке, производится для увеличенного сечения в один этап, как при поверочных расчетах.