Формы описания динамических свойств объектов

Динамические свойства объектов в общем случае можно описать математическими выражениями следующего вида:

1) дифференциальными уравнениями

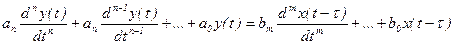где 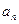, …, , , 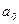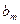…, 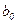- постоянные коэффициенты, m ≤ n;

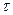- постоянная положительная величина, называемая временем запаздывания;

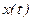- входная величина;

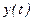- выходная величина,

2) передаточной функцией

,

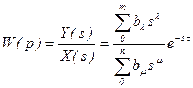где 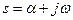- комплексная переменная;

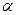- вещественная переменная;

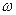- угловая частота;

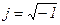- мнимая единица;

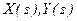- преобразования Лапласа;

3) амплитудно-фазовой характеристикой (АФХ)

,

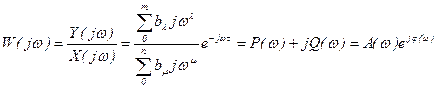где 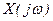, 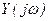- преобразования Фурье переменных 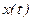и ;

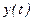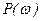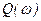, - аналитические выражения вещественных и мнимых частей комплексной функции ;

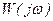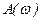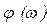, - амплитудно-частотная и фазо-частотная характеристики - АЧХ и ФЧХ:

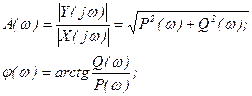
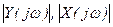- модули (спектры) преобразований Фурье , .

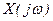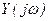Между перечисленными динамическими характеристиками существует однозначная связь.

Взаимосвязь между различного рода динамическими характеристиками изображена на рисунке 4.10, там же указаны способы определения уравнений динамики

<10 11 121314 15 16 >

Дата добавления: 2021-12-14; просмотров: 244;