Индивидуальные задания
Задание 1. Согласно заданному преподавателем варианту нарисуйте схему и диаграмму работы указанного в таблице 4-х счетчика.
| № вар. | Триггер | Установочные входы | Начальная установка | Тип переноса | Счетчик |
| DС | -RS | 5 (высокий) | последовательный | суммирующий | |
| DС | R-S | 6 (низкий) | последовательный | реверсивный | |
| DС | -R-S | 0 (высокий) | параллельный | вычитающий | |
| D-С | RS | 7 (низкий) | параллельный | реверсивный | |
| D-С | -RS | 11 (высокий) | последовательный | вычитающий | |
| СJK | -R-S | 2 (высокий) | параллельный | реверсивный | |
| С-JK | R-S | 3 (низкий) | последовательный | реверсивный | |
| СJ-K | -RS | 6 (низкий) | параллельный | суммирующий | |
| -С-JK | RS | 1 (низкий) | параллельный | реверсивный | |
| -СJ-K | RS | 9 (высокий) | последовательный | вычитающий | |
| С-J-K | R-S | 5 (низкий) | параллельный | суммирующий | |
| -СJ-K | -RS | 2 (высокий) | параллельный | реверсивный | |
| -С-J-K | -R-S | 1 (низкий) | параллельный | вычитающий | |
| СJK | R-S | 7 (высокий) | параллельный | реверсивный | |
| Т | RS | 4 (низкий) | параллельный | суммирующий | |
| Т | -RS | 0 (низкий) | последовательный | реверсивный | |
| Т | R-S | 5 (высокий) | параллельный | суммирующий | |
| Т | -R-S | 3 (низкий) | параллельный | реверсивный | |
| -R-SС | -RS | 1 (низкий) | последовательный | вычитающий | |
| R-SС | RS | 0 (высокий) | параллельный | суммирующий | |
| -RSС | -R-S | 5 (низкий) | последовательный | реверсивный |
Задание 2. Согласно заданному преподавателем варианту нарисуйте схему N-разрядного счетчика. Поясните последовательность подачи управляющих сигналов на диаграмме.
| № вар. | Микросхема | Начальная установка счетчика | Разрядность | Счетчик |
| ИЕ2 | суммирующий | |||
| ИЕ2 | суммирующий | |||
| ИЕ2 | суммирующий | |||
| ИЕ2 | суммирующий | |||
| ИЕ5 | суммирующий | |||
| ИЕ5 | суммирующий | |||
| ИЕ5 | суммирующий | |||
| ИЕ5 | суммирующий | |||
| ИЕ6 | реверсивный | |||
| ИЕ6 | вычитающий | |||
| ИЕ6 | суммирующий | |||
| ИЕ7 | реверсивный | |||
| ИЕ7 | вычитающий | |||
| ИЕ7 | суммирующий | |||
| ИЕ10 | суммирующий | |||
| ИЕ10 | суммирующий | |||
| ИЕ13 | суммирующий | |||
| ИЕ13 | суммирующий | |||
| ИЕ17 | вычитающий | |||
| ИЕ17 | суммирующий | |||
| ИЕ17 | реверсивный |
6. ШИФРАТОРЫ И ДЕШИФРАТОРЫ
Общие сведения
Шифраторы и дешифраторы относятся к комбинационным устройствам, они не имеют внутренней памяти, как и логические элементы. То есть уровни их выходных сигналов всегда однозначно определяются текущими уровнями входных сигналов и никак не связаны с предыдущими значениями входных сигналов. Любое изменение входных сигналов обязательно изменяет состояние выходных сигналов.
Функции дешифраторов и шифраторов понятны из их названий.
Дешифратор преобразует входной двоичный код в номер выходного сигнала (дешифрирует код), а шифратор преобразует номер входного сигнала в выходной двоичный код (шифрует номер входного сигнала).
На выходе дешифратора всегда присутствует только один сигнал, причем номер этого сигнала однозначно определяется входным кодом. Выходной код шифратора однозначно определяется номером входного сигнала.
Дешифраторы
Дешифратор – это комбинационное устройство, позволяющее распознавать числа, представленные позиционным n-разрядным кодом.
Полным дешифратором называется дешифратор с n выходами, который позволяет распознавать 2n чисел.
Если число выходов дешифратора не позволяет распознавать 2n чисел, то такой дешифратор называют неполным.
Иначе дешифратор называют преобразователем позиционного кода в унитарный.
Унитарным кодом называют код, в котором только в одном его разряде есть логическая 1 (для прямых выходов), а в остальных нули.
Процесс распознавания дешифратором двоичных чисел заключается в том, что в зависимости от набора кода поступившего на вход дешифратора, сигнал 1 появится только на одном его выходе.
Микросхемы дешифраторов обозначаются на схемах буквами DC (от английского Decoder).
Функциональная схема дешифратора представлена на Рис.6.1.
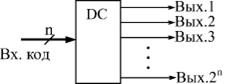
|
| Рис.6.1. Функциональная схема дешифратора |
Дешифраторы применяются для расшифровки адресов ячеек запоминающих устройств, высвечивание букв и цифр на дисплеях и т.д.
В зависимости от разрядности дешифрируемого кода и функциональных возможностей интегральных схем (ИС), имеющихся в распоряжении разработчика, дешифратор может быть выполнен на основе одноступенчатой (линейной) или многоступенчатой схем дешифрации.
В таблице 6.1. показана таблица истинности m входового дешифратора. Данный дешифратор имеет m входов и n выходов.
| Входы | Выходы | |||||||||||
| Х1 | Х2 | Х3 | Хm-1 | У0 | У1 | У2 | У3 | У4 | У5 | Y n-1 | ||
| … | … | |||||||||||
| … | … | |||||||||||
| … | … | |||||||||||
| … | … | |||||||||||
| … | … | |||||||||||
| … | … | |||||||||||
| … | … | |||||||||||
| … | … |
Линейные дешифраторы выполняются прямой схемной реализацией системой логических выражений вида:
| Y0 | = | Х0 | * | Х1 | * | Х2 | *…* | Хm-1 | (1) |
| (1) | |||||||||
| Y1 | = | Х0 | * | Х1 | * | Х3 | *…* | Х m-1 | (2) |
| Y2 | = | Х0 | * | Х1 | * | Х3 | *…* | Х m-1 | (3) |
| … | |||||||||
| Y n-1 | = | Х0 | * | Х1 | * | Х3 | *…* | Х m-1 | (n) |
где Y0, Y1,…. ,Yn-1 – выходные логические функции; X1, X2,..., Xm-1; X1, X2,..., Xm-1 – входные логические переменные и их отрицания; * – знак логического умножения; n=2m – множество комбинаций входных переменных (число выходов полного дешифратора).
Таким образом, линейный дешифратор представляет собой 2m независимых по выходам вентилей с m входами каждый. На рисунке 6.2 показана схема четырехразрядного линейного дешифратора.
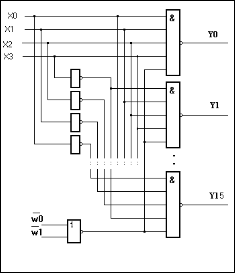
Рисунок 6.2. Функциональная схема линейного четырехразрядного
двоичного дешифратора
Одноступенчатые линейные дешифраторы эффективны, когда разрядность входного кода не превышает числа входов схемы И типового логического элемента ИС.
Линейный одноступенчатый дешифратор обладает самым высоким быстродействием в сравнении с другими типами дешифраторов.
В отечественных сериях микросхемы дешифраторов обозначаются буквами ИД. На рис. 6.6 показаны наиболее типичных микросхемы дешифраторов.
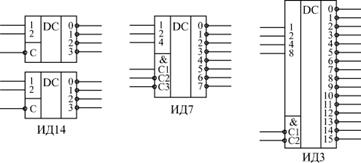
Рисунок 6.6. Примеры микросхем дешифраторов
Код на входах 1, 2, 4, 8 определяет номер активного выхода (вход 1 соответствует младшему разряду кода, вход 8 — старшему разряду кода). Входы разрешения С1, С2, С3 объединены по функции И и имеют указанную на рисунке полярность.
Дата добавления: 2021-12-14; просмотров: 700;











