Нормальные и касательные напряжения

Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат: нормальное напряжение (σ - сигма), направленное по перпендикуляру к площадке, и касательные напряжения (τ - тау), лежащие в плоскости сечения.

Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону. Часто используют значения: 1 МПа = 10⁶ Па. В технической системе единицы напряжения измеряются в килограммах силы на миллиметр в квадрате (кгс/мм²).

3.9.Напряжения при растяжении и сжатии.В поперечных сечениях при растяжении-сжатииимеют место только нормальные напряжения σ, которые определяются отношением внутренней силы N к площади A соответствующего поперечного сечения стержня.

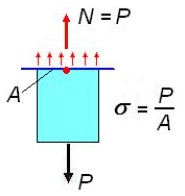
Напряжения в поперечном сечении при растяжении

Знак напряжений зависит от знака внутренней силы на рассматриваемом участке стержня. Для обеспечения необходимой прочности элементов и конструкций напряжения не должны превышать допустимых значений. При растяжении и сжатии в сечении действует только нормаль­ное напряжение. Напряжения могут рассматриваться как силы, приходящиеся на единицу площади.

Таким образом, направление и знак напряжения в сечении со­впадают с направлением и знаком силы в сечении.

Нормальное напряжение можно рассчитать по формуле:

P N

σ _═ ― ═ ― ,

A A

где:

Р - внешняя сила,

N - внутренняя продольная сила в сечении,

А - площадь поперечного сечения.

Таким образом: величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.

Нормальные напряжения действуют при растяжении от сечения, а при сжатии к сечению.

Размерность напряжений: Н/м² (Па), од­нако это слишком малая единица, и практически напряжения рас­считывают в Н/мм² (МПа):

1 МПа = 10⁶ Па = 1 Н/мм².

При определении напряже­ний брус разбивают на участки, в пределах которых продольные силы не изменяются.

Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений. Строится и оформляется такая эпюра так же, как и эпюра про­дольных сил.

Эпюра (чертёж) - это график, который показывает распределение величины нагрузки на объект. Например, для бруса продольная ось симметрии принимается за ось ординат, а по оси абсцисс откладываются значения: вверх (положительные), вниз (отрицательные) значения нагрузок: продольных сил и напряжений. То есть эпюра - это график изменения внутреннего силового фактора по длине бруса. Инженеры-механики чаще используют понятие брус, а инженеры-строители используют понятие стержень, который является частью рам или ферм. Допустимо использовать оба этих понятия.

Расчёт эпюр напряжения является базовой задачей такой дисциплины, как сопротивление материалов. В частности, только при помощи эпюры возможно определить максимально допустимую нагрузку на материал.

Расчет нормальных напряжений при растяжении-сжатии производится по формуле 1. Растяжением - сжатием называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила N. Продольной силой называется равнодействующая всех внутренних нормальных сил, возникающих в этом сечении.

Продольная сила в любом сечении бруса определяется методом сечений: она равна алгебраической сумме проекций всех внешних сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось. Если продольная сила по всей длине бруса не постоянна, то строят эпюру «N».

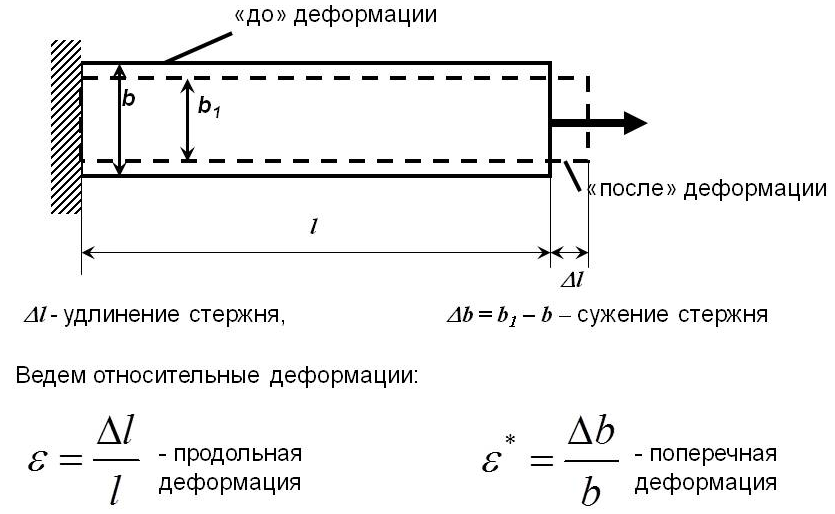
3.10.Продольные и поперечные деформации.Пусть в результате деформации первоначальная длина стержня L станет равной L₁. Изменение длины:

∆ L ═ L₁ ̶ L,

называется абсолютным удлинением стержня.

Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением или продольной деформацией.

Продольная деформация – это безразмерная величина. Формула для определения продольной деформации:

∆ L

ε ═ ―

L

При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.

Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются.