Параллельные прямые

Две прямые на плоскости называются параллельными, если они не пересекаются.

Ранее указанная аксиома параллельности прямых выражает основное свойство параллельных прямых.

Теорема: Две прямые, параллельные третьей, параллельны между собой

Доказательство: самостоятельно

При пересечении двух прямых секущей образуются следующие пары углов:

(укажите их)

Внутренние накрестлежащие – 2 пары

( )

Внутренние односторонние – 2 пары

( )

Соответственные – 4 пары

( )

Признаки параллельности прямых:

1. Если внутренние накрестлежащие углы равны, то прямые параллельны

2. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны

3. Если соответственные углы равны, то прямые параллельны.

Следствие: Две прямые, перпендикулярные к одной и той же прямой, параллельны между собой.

Для признаков параллельности прямых справедливы и обратные теоремы, которые являются свойствами параллельных прямых. Сформулируйте их

1.

2.

3.

Теорема Фалеса: Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство: Пусть |A₁A₂|=|A₂A₃|, где А₁ А₂ А₃ – точки пересечения параллельных прямых с одной стороной угла, и А₂ лежит между А₁ и А₃. Нужно доказать, что |В₁В₂|=|В₂В₃|, где В₁ В₂ В₃ – соответственно точки пересечения параллельных прямых с другой стороной угла. Через точку В₂ проведем прямую EF, параллельную А₁А₃. Тогда четырехугольник А₁А₂В₂F является параллелограммом. По свойству параллелограмма А₁А₂=FВ₂. Аналогично параллелограммом является четырехугольник А₃А₂В₂Е, и В₂Е=А₂А₃. Отсюда получаем, что В₂F=B₂E. Рассмотрим треугольники DВ₂В₁F и DЕВ₂В₃ они равны

(поясните почему:

)

следовательно, В₁В₂=В₂В₃.

Теорема: Два угла, стороны которых соответственно параллельны, равны, или их сумма равна 180°, смотря по тому, имеют ли оба угла одинаковое или различные направления.

Доказательство: Рассмотрим все возможные случаи расположения таких углов:

1) 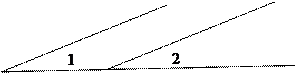Очевидно, что Ð1=Ð2 как соответственные углы при параллельных прямых.

2) 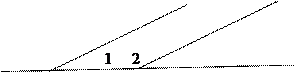Ð1+Ð2=180° как односторонние углы при параллельных прямых

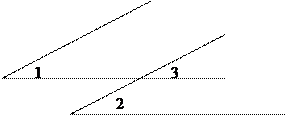
3) Ð1=Ð3 как соответственные углы при параллельных прямых.

Ð2=Ð3 как соответственные углы при параллельных прямых.

Следовательно, Ð1=Ð2.

4) Ð2=Ð3 как соответственные углы при параллельных прямых

Ð1+Ð3=180° как односторонние углы при параллельных прямых

Следовательно, Ð1+Ð2=180°.

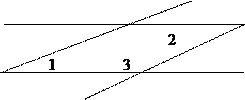
5) Ð1+Ð3=180° как односторонние углы при параллельных прямых

аналогично Ð2+Ð3=180°

Отсюда получаем что Ð1=Ð2.

Теорема: Два угла, стороны которых соответственно перпендикулярны друг другу, равны, или их сумма равна 180°, в зависимости от того, имеют ли оба угла одинаковое направление или различные.

Доказательство: самостоятельно