Синтаксическая мера информации
Эта мера количества информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту.
Объем данных Vдв сообщении измеряется количеством символов (разрядов) в этом сообщении. В различных системах счисления один разряд имеет различный вес и соответственно меняется единица измерения данных:
§ в двоичной системе счисления единица измерения – бит (bit – binary digit – двоичный разряд);
Примечание. В современных ЭВМ наряду с минимальной единицей измерения данных "бит" широко используется укрупненная единица измерения "байт", равная 8 бит.
§ в десятичной системе счисления единица измерения – дит (десятичный разряд).
Пример2.3. Сообщение в двоичной системе в виде восьмиразрядного двоичного кода 10111011 имеет объем данных Vд = 8 бит.
Сообщение в десятичной системе в виде шестиразрядного числа 275903 имеет объем данных Vд = 6 дит.
Количество информации I на синтаксическом уровне невозможно определить без рассмотрения понятия неопределенности состояния системы (энтропии системы). Действительно, получение информации о какой-либо системе всегда связано с изменением степени неосведомленности получателя о состоянии этой системы. Рассмотрим это понятие.
Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе a. Мерой его неосведомленности о системе является функция Н(a), которая в то же время служит и мерой неопределенности состояния системы.
После получения некоторого сообщения b получатель приобрел некоторую дополнительную информацию Ib(a), уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения b) неопределенность состояния системы стала Hb(a).
Тогда количество информации Ib(a) о системе, полученной в сообщении b, определится как
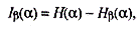
т.е. количество информации измеряется изменением (уменьшением) неопределенности состояния системы.
Если конечная неопределенность Hb(a) обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации Ib(a) = Н(a). Иными словами, энтропия системы H(a) может рассматриваться как мера недостающей информации.
Энтропия системы H(a), имеющая N возможных состояний, согласно формуле Шеннона, равна:
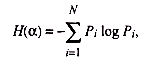
где Pi – вероятность того, что система находится в i-м состоянии.
Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны 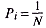 , ее энтропия определяется соотношением
, ее энтропия определяется соотношением
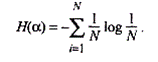
Часто информация кодируется числовыми кодами в той или иной системе счисления, особенно это актуально при представлении информации в компьютере. Естественно, что одно и то же количество разрядов в разных системах счисления может передать разное число состояний отображаемого объекта, что можно представить в виде соотношения
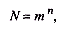
где N – число всевозможных отображаемых состояний;
т – основание системы счисления (разнообразие символов, применяемых в алфавите);
п – число разрядов (символов) в сообщении.
Пример 2.4. По каналу связи передается n-разрядное сообщение, использующее т различных символов. Так как количество всевозможных кодовых комбинаций будет N = mn, то при равновероятности появления любой из них количество информации, приобретенной абонентом в результате получения сообщения, будет I = logN = п log т – формула Хартли.
Если в качестве основания логарифма принять т, то I = п. В данном случае количество информации (при условии полного априорного незнания абонентом содержания сообщения) будет равно объему данных I = Vд, полученных по каналу связи. Для неравновероятных состояний системы всегда I < Vд = п.
Наиболее часто используются двоичные и десятичные логарифмы. Единицами измерения в этих случаях будут соответственно бит и дит.
Коэффициент (степень) информативности (лаконичность) сообщения определяется отношением количества информации к объему данных, т.е.
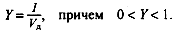
С увеличением Y уменьшаются объемы работы по преобразованию информации (данных) в системе. Поэтому стремятся к повышению информативности, для чего разрабатываются специальные методы оптимального кодирования информации.
Дата добавления: 2021-12-14; просмотров: 472;











