Метод стоимостных регрессионных зависимостей.

Этот метод основан на построении приближенных зависимостей между затратами на создание и эксплуатацию продукции данного вида (или пропорциональными им показателями) и показателями качества продукции. Метод целесообразно применять в тех случаях, когда имеющееся число сравниваемых вариантов продукции достаточно велико и превосходит число выбранных показателей.

Вид зависимости, как правило, выбирают соответственно, используемому комплексному показателю качества. Например, для среднего взвешенного геометрического показателя для построения регрессионной зависимости между затратами и показателями качества следует использовать следующее выражение

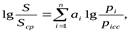
где S_ср и p_ср - величины, полученные усреднением по всем вариантам продукции фактических затрат ипоказателей качества;

a_i – параметры апроксимации, определяемые методом “наименьших квадратов”.

В этом случае параметры апроксимации являются коэффициентами весомости.

Например, сравнивается N вариантов двигателей. Каждый вариант характеризуется набором из (n+1) показателей качества: p_1k , p_2k , …, p_nk , S_k .

Показатели p_ik при увеличении своего значения характеризуют улучшение качества двигателя (мощность, крутящий момент, КПД, средний ресурс и т.п.); S_k –показатель качества двигателя, уменьшение которого характеризует улучшение качества двигателя (общая масса, затраты на производство и эксплуатацию и т.п.).

Предполагая, что для комплексной оценки уровня качества двигателей будет использоваться средний взвешенный геометрический показатель, построим линейную регрессионную зависимость между логарифмами показателя S_k и логарифмами показателей качества p_1k , p_2k , …, p_nk. Выражение для линейной регрессионной зависимости имеет вид

,

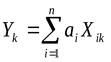
где a_i – коэффициент весомости показателя p_i;

;

;

;

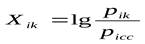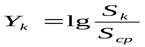
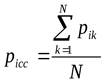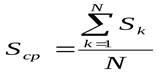Параметрыa_i определяются методом наименьших квадратов..