Основные расчетные выражения и необходимые пояснения

Электропроводность. Проводниковые, полупроводящие и изоляционные материалы

Основные расчетные выражения и необходимые пояснения

Электропроводность – это способность вещества проводить электрический ток, обусловленная наличием свободных зарядов в веществе. Для численного определения этой способности вводятся величины: «удельное электрическое сопротивление», ρ и «удельная электрическая проводимость», γ. Эти величины являются обратными по отношению друг к другу:

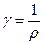(2.1.)

Значение удельной электрической проводимости вещества – γ [См/м]определяется как произведение суммарного заряда свободных носителей в единице объема nq [Кл/м³] и подвижности этих зарядов – u [м²/с×В]:

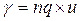[1] (2.2)

n – концентрация свободных зарядов, [1/м³], q – заряд носителя, [Кл].

Удельное электрическое сопротивление, ρ – это параметр вещества, численно равный сопротивлению образца длиной 1 м с площадью поперечного сечения 1 м², измеренному в плоско-параллельном поле.

Удельное электрическое сопротивление измеряется в [ 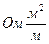] или в [Ом×м]. Удельная электрическая проводимость измеряется в [См/м].

По значению удельного электрического сопротивления все вещества подразделяются на 3 класса:

Проводники………………………………………..…ρ ≈ 10^-8…10^-6 Ом×м;

Слабопроводящие материалы (полупроводники)…ρ ≈ 10^-6…10⁷ Ом×м;

Диэлектрики (изоляционные материалы)………….ρ ≈10⁶…10²⁰ Ом×м.

В электропроводном материале вместо электростатического поля электрических зарядов (которое рассматривалось в теме 1) существует электрическое поле тока, протекающего по материалу. Виды полей, встречающихся в задачах раздела 2 те же, что и в разделе 1. Но для электропроводного материала формулы будут выглядеть следующим образом:

Для плоско-параллельного поля, проводимость конструкции, имеющей площадь поперечного сечения S и длину d, будет равна:

, (2.3)

где

g - удельная электропроводность материала.

Поскольку проводимость есть величина, обратная сопротивлению: 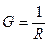, а удельная электропроводность обратная удельному электрическому сопротивлению 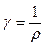, то формула 2.3 идентична хорошо известной:

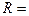r ,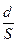

где: - S - площадь поперечного сечения проводника; d - длина проводника.

Для радиально цилиндрического поля, сохраняя те же, что в разделе 1 обозначения геометрических размеров, напишем выражение для проводимости между двумя коаксиальными цилиндрами:

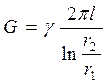, (2.4)

из которого также несложно получить выражение для сопротивления:

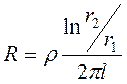
В радиально-сферическом поле потенциал шара, с которого стекает ток в "бесконечность", будет выражаться как:

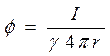, (2.5)

где I - ток, стекающий с шарового электрода радиуса r.

Проводимость между двумя концентрическими (имеющими общий центр) сферами радиусов r₁ и r₂ :

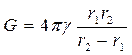, (2.6)

Сравнивая выражения раздела 1 и 2 нетрудно установить их полную аналогию. В том и другом случае при одинаковых полях одинаковы и части выражений, содержащие геометрические параметры. Если независимо от вида поля эти части выражений обозначить буквой Г, то будем иметь два аналогичных выражения:

Для электростатического поля Для поля электрического тока

в диэлектрике: в проводнике:

С = e₀eГ G = gГ (2.7)

 

Если материал конструкции между электродами имеет большое удельное сопротивление и определенное значение диэлектрической проницаемости, то для такой конструкции справедливо вытекающее из (2.7) выражение:

CR = e₀er (2.8)

Левая часть этого выражения есть постоянная времени разряда конденсатора с ёмкостью С через сопротивление R. Правая часть называется постоянной времени релаксации:

τ = e₀er.

Время релаксации отражает скорость затухания возбуждения в материале после исчезновения электрического поля, вызвавшего это возбуждение.

 

В некоторых заданиях раздела затрагивается тема создания композиционных материалов, электропроводность и диэлектрическая проницаемость которых определяются соотношением не реагирующих между собой компонентов с различными значениями указанных величин.

Композиционным материалом называется материал, состоящий из двух или более компонентов, химически не связанных между собой, но в итоге изменяющих параметры материала в целом по сравнению с параметрами каждого из компонентов.

Примеры: бетон, текстолит, гетинакс, эком, бетэл, вилит, резина, стеклопластик, некоторые материалы для электрических контактов, магнитодиэлектрики и др.

Если сравнить между собой формулы разделов 1 и 2 настоящего задачника, то мы увидим их полную идентичность. Поэтому электро-проводность и диэлектрическую проницаемость можно считать аналогичными величинами и присвоить им единое название - “обобщенная проводимость”. Будем обозначать это понятие общим символом “s“, понимая в каждом конкретном случае под ним или диэлектрическую проницаемость или электропроводность.

Если смешивать два вещества с разными значениями s, то возможно образование двух структур: “матричная система” и “статистическая смесь”.

В матричной системе один из материалов образует непрерывную матрицу, в которую вкраплены включения другого материала. Значение обобщенной проводимости для матричной смеси определяется выражением:

 

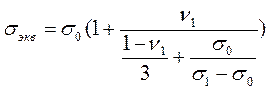
, (2.9)

 

 

в котором s₀ и s₁ - обобщенные проводимости матричной фазы и наполнителя, n₁ - объемная доля наполнителя (в долях единицы).

В статистической смеси оба материала равноправны, и значение обобщенной проводимости рассчитывается по выражению:

 

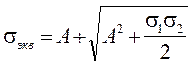
где

 

,

 

 

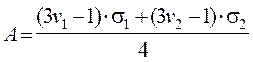
(2.10)

 

 

Пользуясь выражениями, приведенными выше, можно вычислить необходимые параметры всех заданий раздела 2.

 

12

---

Дата добавления: 2016-06-05; просмотров: 1645;

---