Вторая форма условий равновесия
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось, неперпендикулярную прямой АВ, были равны нулю:
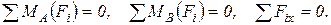 (6.4)
(6.4)
Необходимость этих условий очевидна, так как если любое из них не выполняется, то или 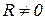 , или
, или 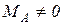 и равновесия не будет. Докажем достаточность.
и равновесия не будет. Докажем достаточность.
Если для рассматриваемой системы сил выполняется первые два условия из (6.4), то MA=0, MB=0. При этом данная система может иметь 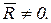 Покажем, что это не так.
Покажем, что это не так.
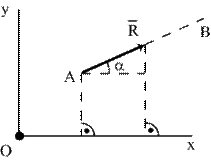
| Из условия 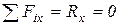 следует, что следует, что 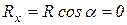 (рис. 6.4).
Но (рис. 6.4).
Но 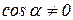 , так как ось ОX не перпендикулярна прямой, проходящей через точки А и В.
Следовательно, равнодействующая R , так как ось ОX не перпендикулярна прямой, проходящей через точки А и В.
Следовательно, равнодействующая R
|
| Рис.6.4 |
равна нулю, что и доказывает достаточность условий (6.4).
Вторую форму уравнений равновесия удобно применять для шарнирно опертых балок. Рассмотрим для примера равновесие балки АВ, нагруженной, как показано на рис.6.5а, опертую на шарнирно-подвижную опору в точке А и шарнирно-неподвижную опору в точке В. Дано: P = 10 kН, q = 4 kН/м, L = 6 м, a = 30°.
Используя метод сечения, отбросим связи и заменим их соответствующими реакциями (рис.6.5б). Распределенную нагрузку интенсивностью q заменим ее равнодействующей. Запишем уравнения равновесия (6.4) для заданной системы сил:
| а | 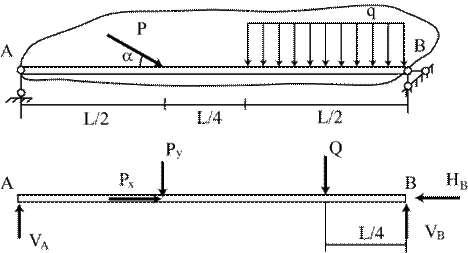
|
| б | |
| Рис.6.5 |
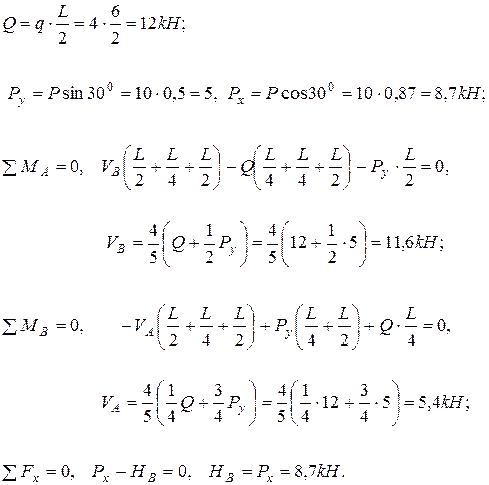
Сделаем проверку. Ясно, что при равновесии проекции сил на ось Y также должны быть равны нулю.
Проверим это:
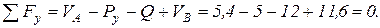
Дата добавления: 2019-12-09; просмотров: 465;











