Радиусы колес автомобиля

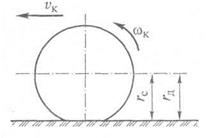
У колес автомобиля (рис. 3.4) различают следующие радиусы: статический r_с,динамический r_д и радиус качения r_кач.

Статическим радиусом называется расстояние от оси непод­вижного колеса до поверхности дороги. Он зависит от нагрузки, приходящейся на колесо, и давления воздуха в шине. Статичес­кий радиус уменьшается при возрастании нагрузки и снижении давления воздуха в шине, и наоборот.

Динамическим радиусом называется расстояние от оси катяще­гося колеса до поверхности дороги. Он зависит от нагрузки, дав­ления воздуха в шине, скорости движения и момента, передавае­мого через колесо. Динамический радиус возрастает при увеличе­нии скорости движения и уменьшении передаваемого момента, и наоборот.

Радиусом качения называется отношение линейной скорости оси колеса к его угловой скорости:

.

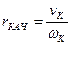Радиус качения, зависящий от нагрузки, давления воздуха в шине, передаваемого момента, пробуксовывания и проскальзы­вания колеса, определяется экспериментально или вычисляется по формуле

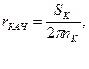(3.13)

где п_к — число полных оборотов колеса; S_K — путь, пройденный колесом за полное число оборотов.

Из выражения (3.13) следует, что при полном буксовании ко­леса (S_K = 0) радиус качения r_кач = 0, а при полном скольжении

(n_к = 0) r_кач →∞.

Как показали исследования, на дорогах с твердым покрытием и хорошим сцеплением радиус качения, статический и динами­ческий радиусы отличаются друг от друга незначительно. Поэтому можно считать, что они практически равны, т.е. r_с ≈ r_д ≈ r_кач.

При выполнении расчетов в дальней­шем будем использовать это приближен­ное значение. Соответствующую вели­чину назовем радиусом колеса и обо­значим r_к.

Для различных типов шин радиус колеса может быть определен по ГОСТ, в котором регламентированы статичес­кие радиусы для ряда значений нагруз-

ки и давления воздуха в шинах. Кроме того, радиус колеса, м, можно рассчитать по номинальным размерам шины, используя выражение

r_к = 0,5d +λ_шВ_ш, (3.14)

где d — диаметр обода колеса, м; В_ш — ширина профиля шины, м; λ_ш= 0,8...0,9 — коэффициент смятия шины.

Формула (3.14) обеспечивает наиболее точные результаты для самого распространенного типа шин — тороидальных.