Модель однородного пласта.

В этой модели основные параметры реального пласта (пористость, проницаемость), изменяющиеся от точки к точке, усредняют. Модель однородного пласта используют для пластов с небольшой неоднородностью.

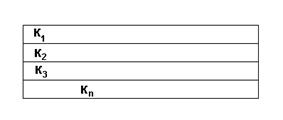
Модель слоистого пласта.

Эта модель состоит из набора прослоев различной проницаемости и характеризуется той же функцией распределения проницаемости, что и реальный пласт.

Модель трещиноватого пласта.

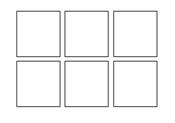
Если нефть залегает только в трещинах, то модель такого пласта может быть представлена в виде набора непроницаемых кубов, грани которых разделены щелями. Подбирается средняя густота трещин и их средняя ширина как и в реальном пласте. Нефть идет только по трещинам, матрица является непроницаемой.

Модель трещиновато-пористого пласта.

Модель аналогична предыдущей, только фильтрация жидкостей и газов идет как по трещинам, так и по блокам (матрицам).

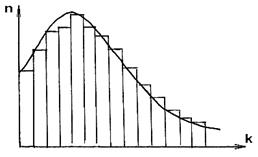
Наиболее распространены модели слоистого пласта. Главной задачей таких моделей является подбор соответствующей функции распределения проницаемости, которая была бы как в реальном пласте. Для этого используют фактические данные по керну или по геофизическим данным. По этим данным строят гистограмму распределения проницаемости по пласту, где ступенька это доля общей толщины пласта с соответствующей проницаемостью.

Исходя из этой гистограммы, подбирают соответствующую аналитическую зависимость (функцию).

В случае несоответствия теоретических и фактических данных эти функции изменяют до получения совпадения теоретических и фактических показателей разработки, т.е. модель пласта адаптируют к фактическому процессу разработки.

При вероятностно-статистическом описании пластов наиболее важны это плотность статистического распределения, которая отражает вероятность появления слоя, изменяющегося в каких то пределах и функция или закон распределения параметра.

Для вероятностно-статистического описания распределения проницаемости пласта, пористости, изменения толщин продуктивных пластов и других параметров, изменяющихся от точки к точке, в нефтяной залежи применяют следующие законы распределения: Закон Гаусса или нормальный закон распределения, логарифмически нормальный закон, гамма – распределение, закон распределения Максвелла.

Для закона Гаусса плотность распределения проницаемости выражается следующей зависимостью

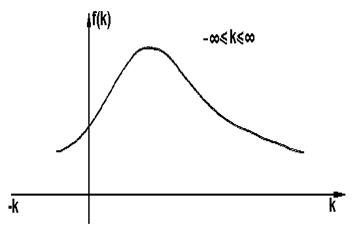
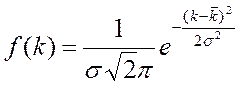, где

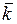- средняя проницаемость,

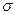- параметр распределения

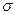² - среднеквадратичное стандартное отклонение, характеризует рассеянность значений анализируемых параметров относительно их средних значений. Чем больше 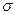, тем больше рассеянность значений параметра. 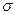определяют по формуле:

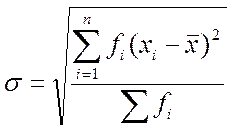, где

х_i (х₁,х₂…..х_n) – отдельные величины параметра;

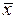- среднеарифметическая величина;

f_i (f₁, f₂…f_n) – число случаев (частота) параметра.

Среднеарифметическая взвешенная величина параметра х характеризует среднюю величину анализируемого параметра и вычисляется по формуле:

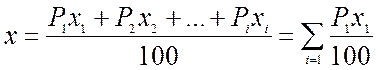, где

Р₁, Р₂… Р_n – процент скважин, имеющих величину параметра в интервале

значений х₁, х₂….х_n.

Коэффициент вариации v представляет отношение среднеквадратичного отклонения к среднеарифметическому значению анализируемого параметра:

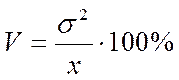
и является относительной мерой колебания параметра.

Указанные статистические параметры служат показателями степени неоднородности таких параметров пласта, как пористость, проницаемость, степень изменчивости толщин продуктивных пластов.

При построении моделей трещиноватого или трещиновато-порового пласта необходимо знать средний размер блока породы или густоту трещин, а также проницаемость, которая в трещиноватом пласте определяется раскрытием трещин. Эти параметры устанавливают по данным гидродинамических исследований скважин. Модели пластов наиболее соответствующие действительности, могут быть построены лишь на основе тщательного изучения и учета свойств пласта и сопоставления результатов расчета, процесса разработки пласта с фактическими данными. В последние годы в связи с ростом вычислительно-компьютерных возможностей получают большое развитие адресные модели пластов и процессов разработки.

Свойства горных пород, пластовых жидкостей и газов,

учитываемые при моделировании

При моделировании используются параметры свойств горных пород, пластовых жидкостей и газов. В начале используются данные керна, полученного при бурении скважин и глубинные пробы нефти и газа. Затем эти свойства определяются путем обработки данных геофизических и гидродинамических исследований, т.к. для расчетов нужны не только первоначальные данные, но и полученные в процессе разработки.

Горное напряжение.

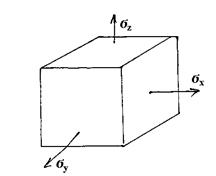
Все породы, в том числе и нефтеносные пласты, находятся постоянно в напряженном состоянии. Выделим из горных пород мысленно элементарный объем в виде куба.

Если ось z направлена по вертикали, а x и y по горизонтали, то нормальное напряжение σ_Ζ = Р_Г и характеризует горное или геостатическое давление.

Компоненты σ_x σ_y= σ_б- отражают боковое горное давление.

Считается, что при пологом залегании пластов горное давление Р_Г = γН , где 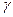удельный вес горных пород, Н –глубина залегания пласта.Боковое горное давление определяется

σ_б= αР_Г

где а – коэффициент бокового горного давления, который может изменяться в широких пределах. Если залежь нефтенасыщенна, то в пласте действует и внутрипоровое давление Рпл, создаваемое жидкостью или газом. Напряженное состояние характеризуется средним нормальным напряжением

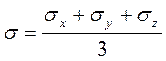
Между вертикальным горным давлением, средним нормальным напряжением и внутрипоровым давлением существует связь

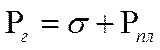
Экспериментально доказано, что

с увеличением среднего напряжения ( 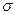) К(проницаемость) и m(пористость) уменьшаются. Скелет породы находится под действием эффективного напряжения:

Р_эф. = Р_г – Р_пл .

2. давление насыщения.

Мы знаем, что в пласте находится какое-то количество нефти, газа и воды. При разработке месторождений необходимо количественно прогнозировать их отбор. Для этого надо знать фазовое состояние, насыщающих пласт флюидов, а оно постоянно меняется. При уменьшении t° и Р газ может выделяться из нефти или наоборот растворяться в ней.

При расчете фазового состояния нефть условно разделяется на 2 компонента «нефть» и «газ».

Газ растворяется в нефти по закону Генри:

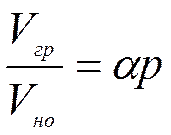, где

V_гр – объем растворенного газа;

V_но – объем дегазированной нефти;

α - коэффициент пропорциональности;

p – давление.

То согласно закону при некотором давлении,_, которое называется Р насыщения весь газ будет растворен в нефти.

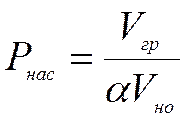
3. Важнейшим свойством при разработке месторождений является вязкость (µ) жидкости и газа. Вязкость нефти в пласте уменьшается с ростом температуры и увеличении объема растворенного газа. При водонапорном режиме, на эффективность процесса влияет соотношение:

.

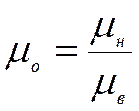При разработке нефтяных месторождений широко используется ряд параметров, которые одновременно характеризуют 2-3 основных свойства продуктивного пласта.

Коэффициент гидропроводности

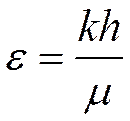, где

k – проницаемость пласта;

h - эффективная (работающая) толщина пласта;

µ - вязкость жидкости и газа.

Гидропроводность или коэффициент гидропроводности представляет емкую характеристику продуктивного пласта, определяющую его производительность.

Коэффициент проводимости или подвижности нефти, характеризующий подвижность жидкости в пластовых условиях в зависимости от ее вязкости (µ) и проницаемости пласта k :

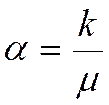
Коэффициент пьезопроводности:

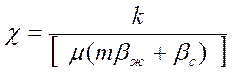, где

m – пористость пласта;

b_ж и b_с – коэффициенты сжимаемости пластовой жидкости и пористой среды.

Коэффициент пьезопроводности характеризует скорость перераспределения давления в пласте.