Принципы в подсчёте числа комбинации или правила суммы и произведения.

Большинство задач решается с помощью этихдвух принципов.

Принцип суммы. «Если некоторый объект А можно выбрать т способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить (т +n) способами».

Применяется в том случае, когда изучаемые комбинации удаётся разбить на несколько классов, причём каждая комбинация входит в один, и только в один класс.

Пример 1......

Принцип произведения. «Если объект А можно выбрать т способами, и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары «А и В» в указанном порядке можно осуществить (т 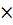n) способами».

Пример 2......

2. Комбинации по типу перестановок, размещений и сочетаний. Такие комбинации встречаются чаще обычного. Рассмотрим их.

2.1. Перестановки. Пусть имеется множество из n элементов. Установленный в некотором множестве порядок называют перестановкой его элементов.

Примеры перестановок: распределение n различных должностей среди n человек или расположение n различных предметов в одном ряду.

Зададимся вопросом: «Сколько различных перестановок можно образовать в множестве из n элементов!» Число перестановок обозначается Р_n (читается "Р из n").

Чтобы вывести формулу числа перестановок, представим себе n ячеек, пронумерованных числами 1,2,...,n. Все перестановки будем образовывать, располагая элементы множества в этих ячейках. В первую ячейку можно занести любой из n элементов (иначе: первую ячейку можно заполнить n различными способами). Заполнив первую ячейку, можно найти (n-1) вариантов заполнения второй ячейки. Таким образом, существует n(n-1) вариантов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти (n-2) варианта заполнения третьей ячейки, откуда получается, что три ячейки можно заполнить n(n-1)(n-2) способами. Продолжая этот процесс, получим, что число способов заполнения n ячеек равно n(n-1)(n-2)·…· 3·2 ·1. Отсюда

Р_n = n(n-1)(n-2)·…· 3·2 ·1.

Число n (n-2)·…· 3·2 ·1, то есть произведение всех натуральных чисел от 1 до n, называется «n-факториал» и обозначается n! Отсюда P_n=n!

По определению считается: 1!=1. Но чему равен 0!=?. Для любого n>1 справедливо
n!=n(n-1)! Положим n=1, тогда 1!=1·0!, следовательно, 0!=1.

Пример 3. Сколько существует вариантов замещения пяти различных вакантных должностей между пятьюкандидатами?

N=5!=5·4·3·2·1=120.

2.2. Размещения.Размещениями из n элементов по т элементов будем называть упорядоченные подмножества, состоящие из т элементов множества, состоящего из n элементов. Число размещений из n элементов по т элементов обозначается 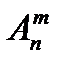(читается "А из n по т ").

Зададимся вопросом: «Сколько упорядоченных подмножеств по т элементов в каждом можно получить из заданного множества в n элементов?»

Одно размещение из n элементов по т элементов может отличаться от другого как набором элементов, так и порядком их расположения.

Примеры задач, приводящих к необходимости подсчета числа размещений. Сколькими способами можно выбрать из пятнадцати человек пять кандидатов и назначить их на пять различных должностей? Сколькими способами можно из двадцати книг отобрать двенадцать и расставить их в ряд на полке?

В задачах о размещениях полагается т < п. В случае если т=n, то легко получить 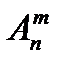= Р_n =n!

Для вычисления 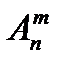используем тот же метод, что использовался для подсчета Р_n только здесь выберем лишь т ячеек. Первую ячейку можно заполнить n способами, вторую, при заполненной первой, можно заполнить (n-1) способами. Таким образом, существует n(n- 1) вариантов заполнения первых двух ячеек. Можно продолжать этот процесс до заполнения последней т -й ячейки. Эту ячейку при заполненных первых (m – 1) ячейках можно заполнить
n – (m – 1) = n – m +1 способами. Таким образом, все т ячеек заполняются числом способов, равным

n(n – 1)(n – 2)... (n – m + 2)(n – m + 1) =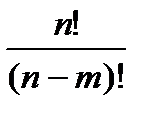

Отсюда получаем: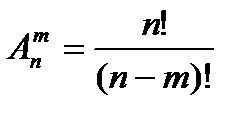

Пример 4. Сколько существует различных вариантов выбора четырёх кандидатур из девяти специалистов для поездки в четыре страны?

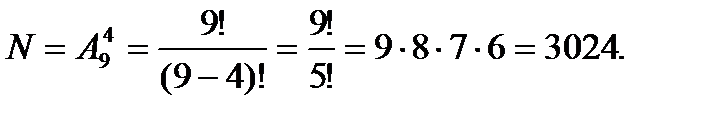
2.3. Сочетания. Сочетаниями из n элементов по т элементов называются подмножества, состоящие из т элементов множества, состоящего из n элементов.

Одно сочетание от другого отличается только составом выбранных элементов, но не порядком их расположения, как у размещений.

Число сочетаний из n элементов по тэлементов обозначается 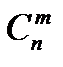(читается "С из n по т ").

Примеры задач, приводящих к подсчету числа сочетаний. Сколько существует вариантов выбора шести человек из пятнадцати кандидатов для назначения на работу в одинаковых должностях? Сколькими способами можно из двадцати книг отобрать двенадцать книг?

Выведем формулу для подсчета числа сочетаний. Пусть имеется множество из n элементов. Образуем подмножество, содержащее т элементов, т.е. сочетание. Известно число упорядоченных подмножеств из т элементов всего множества из n элементов, т.е. размещений из n по т: 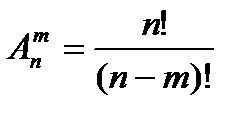. Количество неупорядоченных подмножеств будет в m! раз меньше. Т.е. во столько раз сколькими способами можно установить порядок во множестве из тэлементов. Следовательно, .

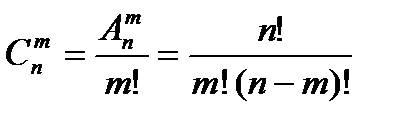Пример 5. Шесть человек из пятнадцати можно выбрать числом способов, равным

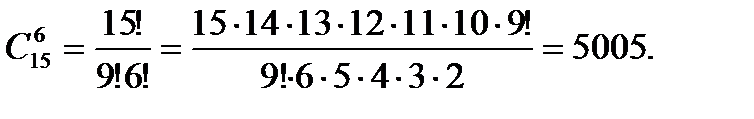
Несложно понять, что осуществить выбор подмножества из т элементов множества, насчитывающего n элементов, можно, выбрав (n - т) элементов, которые не войдут в интересующее нас подмножество. Отсюда следует свойство числа сочетаний

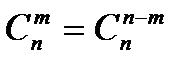
Эту формулу можно легко доказать, используя формулу для числа сочетаний.