Задачи с решениями.

Задача 1. Сколькими различными способами можно расставить на полке собрание сочинений, состоящее из десяти томов, при условии, что первый и пятый тома не должны стоять рядом.

Задача 2. Автокомбинат имеет семь автомобилей малой грузоподъёмности и десять большегрузных автомобилей. Нужно выбрать три автомобиля малой грузоподъёмности для обслуживания трёх торговых организаций и пять большегрузных автомобилей для работы на стройке. Сколькими способами автокомбинат может осуществить свой выбор?

Задача 3. Имеется пять кусков материи разных цветов. Сколько из этих кусков можно сшить различных флагов, если флаги состоят из трёх горизонтальных полос, причём две соседние полосы должны быть разного цвета?

Задача 4. Сколько существует различных вариантов рассадки двенадцати человек за круглым столом, причём один вариант отличается от другого тем, что хотя бы у одного человека при разных вариантах разные соседи слева.

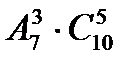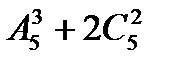Ответы: 1) 8·9!; 2) ; 3) ; 4) 11!

Решение задачи 1. Всего существует 10! различных перестановок десяти книг. Чтобы подсчитать, сколько можно найти перестановок, в которых первый и пятый тома стоят рядом, предположим, что к первому тому приклеен справа пятый том, и они как бы образуют отдельную книгу. Таким образом, получилось девять книг, которые могут быть расставлены 9! способами. Теперь нужно учесть, что первый и пятый тома могут быть склеены в другом порядке, и можно получить ещё 9! различных перестановок десяти книг, в которых первый и пятый тома стоят рядом. Отсюда следует, что ответ задачи составляет число, равное 10! – 2·9! = 8·9!

Решение задачи 2. Один выбор тройки автомобилей малой грузоподъёмности от другого может отличаться не только составом выбранных машин, но и их распределением по торговым организациям. Возможно, что эти торговые организации расположены на различных расстояниях от автокомбината, что у них разные условия оплаты труда и т. п. Таким образом , здесь речь идет о размещениях из семи по три, число которых равно .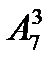

Напротив, выбор тяжелых грузовиков определяется только их составом, так как все они будут работать, как можно заключить из формулировки задачи, в одинаковых условиях. Таким образом, здесь речь идет о сочетаниях из десяти по пять, число которых равно .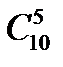

Теперь заметим, что каждый выбор автомобилей малой грузоподъёмности может быть осуществлён при 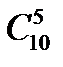различных вариантах выбора тяжёлых грузовиков. Отсюда следует, что выбрать требуемую восьмёрку машин автокомбинат может числом способов, равным .

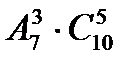Решение задачи 3. Если флаги составлять из трёх полос трёх разных цветов, то один флаг от другого может отличаться не только выбором цветов полос, но и порядком их расположения. Это значит, что из пяти кусков можно изготовить 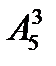различных флагов, состоящих из трёх полос трёх различных цветов.

По условию задачи каждый флаг можно изготовить из полос двух цветов, например, следующих сверху вниз в таком порядке: "красная, белая, красная", или в таком порядке: "белая, красная, белая". Выбор двух цветов можно осуществить числом способов, равным 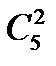и при каждом варианте выбора получить два различных флага.

Из сказанного следует, что всего можно изготовить 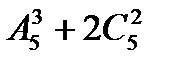различных флагов.

Решение задачи 4.

Заномеруем всех людей числами от 1 до n. Посадим за стол человека с номером 1 на любое место. Будем называть это место первым. Для того, чтобы занять место слева от него (назовём это место вторым) есть n – 1 претендент. Таким образом, мы получаем n – 1 вариант посадки двух человек. Выбрав кого-либо из претендентов на второе место, и обозначив место слева от второго третьим, будем на третье место иметь n – 2 претендента. Отсюда следует, что первые три места можно занять числом способов, равным (n – 1)(n – 2). Действуя таким образом дальше, мы очевидно переберём все способы посадки n человек за круглым столом, и этих способов будет
(n – 1)·(n – 2)·…·3·2 =(n – 1)!