Условия совместной работы элементов ступени, расположенных на различных радиусах

Для достижения высоких значе­ний КПД ступени форма и расположение ее лопаток должны быть хорошо согласо­ваны с формой треугольников скоростей на различных радиусах, т.е., как говорят, лопатки РК и НА должны быть надлежащим образом спрофилированы.

Но окружная скорость лопаток, углы b₁, b₂ и другие параметры треугольников скоростей для различных радиусов существенно различаются в зависимости от того, где они расположены – ближе к втулке или к периферии. И в то же время они связаны между собой. Для определения формы лопаток, потребной для получения высокого КПД, установим эту связь.

Рассмотрим этот вопрос в предположении, что поверхности тока в ступени близки к цилиндрическим, а окружная неравномерность потока воздуха в каналах между рабочими колесами и направляющими аппаратами пренебрежимо мала.

Выделим в осевом зазоре между лопаточными венцами элементарный объем

Т.к. воздух в осевом зазоре закручен, особенно за РК, на данный объем воздуха в радиальном направлении действует центробежная сила

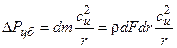
Так как рассматривается течение воз­духа в осевом зазоре, где силовое воздействие лопаток на поток от­сутствует, то единственными внешними силами, имеющими ради­альные составляющие, являются силы давления,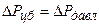

Но

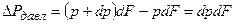
После некоторых преобразований получим уравнение радиального равновесия:

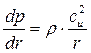(3.6)

Из уравнения (3.6) видно, что в любом межлопаточном канале компрессора, если окружная составляющая скорости воздуха не равна нулю, давление возрастает от втулки к корпусу.

С другой стороны связь между давлением и скоростью воздуха в осевом зазоре на этой поверхности может быть получена из обобщенного уравнения Бернулли.

Рассмотрим тече­ние воздуха вдоль поверхности тока от начального сечения “в” на входе в компрессор до сечения “i”, соответствующего данному осе­вому зазору. В соответствии с урав­нение Бернулли можно записать:

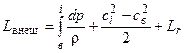, (3.7)

где L_внеш = L_u - работа, сообщенная воздуху на данном радиусе

Примем допущение: входная скоростьc_ви гидравличе­ские потери L_r не меняются по радиусу,

тогда продифференцировав уравнение (3.7) по r, получим (опуская индекс i):

.

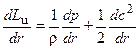Разложив скорость с в данном сечении на составляющие c_а и c_u и заменяя производную dp/dr ее выражением согласно уравнению (3.6), получим окончательно

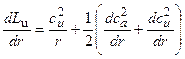. (3.8)

Компрессор обычно проектируется так, чтобы в каждой его ступени работа, сообщаемая воздуху, была неизменна вдоль радиуса. Это позволяет избежать потерь на смешение струек воздуха с различной энергией.

Lu = Dcuu =Dwuu=const

(3.9)

Тогда L_u не зависит от радиуса ( 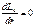), и уравнение (3.8) при­обретает вид:

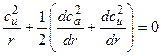. (3.10)