Материальный баланс.
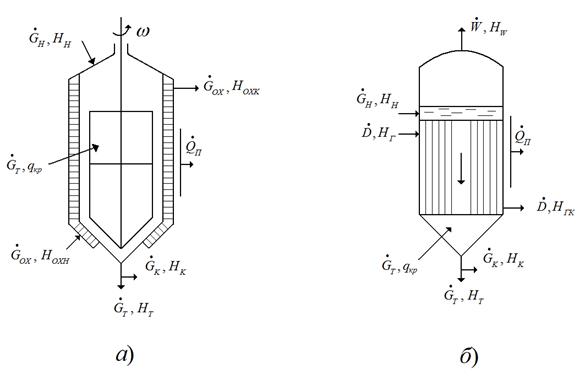
Рис.7.5. Схемы материальных и тепловых балансов кристаллизации:
а – изогидрическая кристаллизация, б – изотермическая кристаллизация.
Материальный баланс процесса кристаллизации по общим потокам веществ может быть представлена в виде:
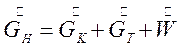 (7.4)
(7.4)
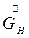 - расход начального раствора,
- расход начального раствора,
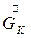 - расход конечного (маточного) раствора,
- расход конечного (маточного) раствора,
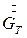 - расход кристаллов (кристаллической фазы),
- расход кристаллов (кристаллической фазы),
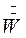 - поток выпаренной воды.
- поток выпаренной воды.
Баланс по безводному веществу имеет вид:
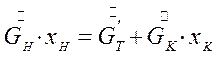 (7.5)
(7.5)
хн – начальная концентрация растворенного вещества в растворе,
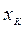 – конечная концентрация растворенного вещества в растворе (маточный раствор).
– конечная концентрация растворенного вещества в растворе (маточный раствор).
Здесь 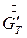 - расход кристаллической фазы в пересчете на растворенное вещества. Определяем
- расход кристаллической фазы в пересчете на растворенное вещества. Определяем 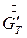 как:
как:
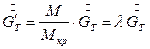 (7.6)
(7.6)
где М- молекулярная масса кристалла без растворителя, 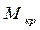 - молекулярная масса кристалла с учетом растворителя. Например, сульфат меди кристаллизуется при Т=50
- молекулярная масса кристалла с учетом растворителя. Например, сульфат меди кристаллизуется при Т=50 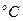 как
как 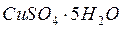 , а при более высоких Т как
, а при более высоких Т как 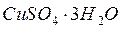 .
.
Решая совместно уравнения (7.4) – (7.6) получим расход кристаллической фазы:
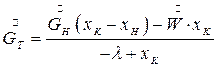 (7.7)
(7.7)
Если кристаллическая фаза не включает растворителя тогда 𝝀=1:
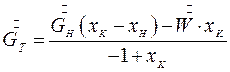 (7.8)
(7.8)
При изотермической кристаллизации происходит удаление влаги из насыщенного раствора. Поэтому концентрации начального и маточного раствора равны. Тогда получим:
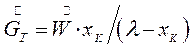 (7.9)
(7.9)
При изогидрической кристаллизации 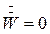 , и уравнение (7.8) примет вид:
, и уравнение (7.8) примет вид:
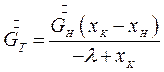 (7.10)
(7.10)
Тепловой баланс.
Тепловой баланс процесса изогридической кристаллизации может быть записан на основе схемы тепловых потоков, представленных на рис.7.5, в виде:
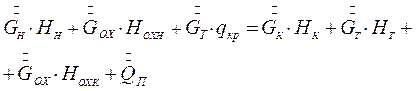 (7.11)
(7.11)
Здесь 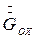 - расход охлаждающей воды,
- расход охлаждающей воды, 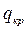 - теплота кристаллизации,
- теплота кристаллизации, 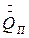 - потери теплоты в окружающую среду, Н – энтальпия, индексы: н – начальный, к – конечный, ох – охлаждающий, т – твердый (кристалл).
- потери теплоты в окружающую среду, Н – энтальпия, индексы: н – начальный, к – конечный, ох – охлаждающий, т – твердый (кристалл).
Уравнения (7.11) и (7.4) дают возможность определить расход охлаждающей воды на процесс изогидрической кристаллизации:
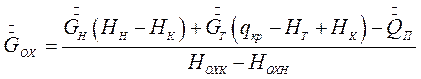 (7.12)
(7.12)
Тепловой баланс изотермической кристаллизации может быть записана основе схемы тепловых потоков, представленных на рис.7.5, в виде:
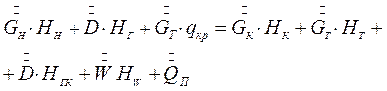 (7.13)
(7.13)
Здесь 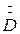 - расход греющего пара;
- расход греющего пара; 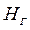 ,
, 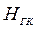 и
и 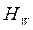 - энтальпии греющего пара, конденсата греющего пара, вторичного пара соответственно.
- энтальпии греющего пара, конденсата греющего пара, вторичного пара соответственно.
Совместное решение уравнений (7.13) и (7.4) позволяет определить расход греющего пара:
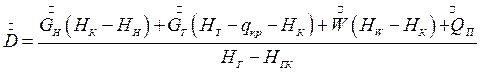 (7.14)
(7.14)
В большинстве случаев при кристаллизации тепло выделяется. В практике кристаллизации теплоту кристаллизации 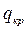 обычно принимает равной по величине и противоположной по знаку теплоте растворения.
обычно принимает равной по величине и противоположной по знаку теплоте растворения.
Дата добавления: 2018-05-10; просмотров: 1175;











