Фильтрование в поле центробежных сил

Движущая сила процесса Dp, от которой зависит интенсивность процесса фильтрования, может быть сформирована при осуществлении процесса в поле центробежных сил – в аппаратах, называемых фильтрующими центрифугами.

Для определения Dp выделим в барабане центрифуги на радиусе r элементарный кольцевой слой толщиной dr, высотой – L (рис. 4.17). Запишем условия равновесия сил для этого элементарного объема суспензии с плотностью r:

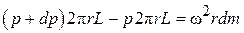
или после сокращения:

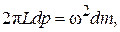(4.31)

где w – угловая скорость вращения барабана,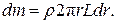

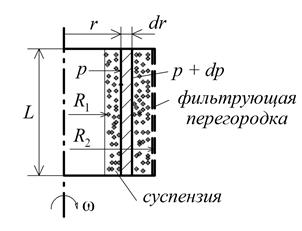
Рис. 4.17. Фильтрование в поле центробежных сил

Интегрируя (4.31) в полных диапазонах изменения Dp
и распределения массы суспензии m, получим:

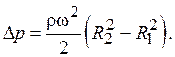(4.32)

За счет Dp происходит процесс центробежного фильтрования.
В ходе работы центрифуги фильтрат проходит через фильтрующую перегородку, и на ее внутренней поверхности образуется слой осадка.

Кольцевой слой осадка располагается в барабане центрифуги
в диапазоне от внутреннего радиуса 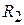цилиндрической фильтровальной перегородки до некоторого переменного во времени внутреннего радиуса 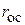высотой L (рис. 4.18).

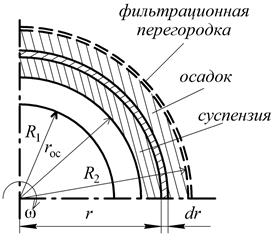
Рис. 4.18. Поперечное сечение фильтрующей центрифуги

Объем осадка для некоторого момента времени t может быть записан:

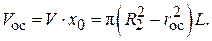(4.33)

Текущее значение 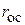может изменяться от 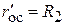в начале процесса 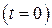до некоторого значения 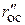в конце него 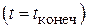. Минимальное значение .

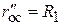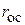Анализируя гидравлическое сопротивление кольцевого слоя осадка , распределенного в диапазоне радиусов от до 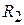, необходимо учесть изменение скорости 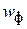по толщине слоя, т.е. по радиальной координате r. Расчет удобно вести на основе скорости 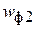, поскольку 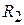всегда известен. Связь текущей скорости 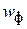со скоростью 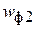можно найти из уравнения расхода:

,

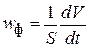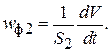
Откуда 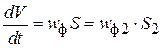и 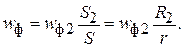(4.34)

Течение фильтрата в порах осадка ламинарное, поэтому для расчета сопротивления осадка можно пользоваться уравнением (4.15).

Несколько видоизменим (4.15) с учетом (4.21):

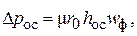(4.35)

где 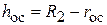– толщина осадка.

Запишем уравнение (4.35) для слоя осадка толщиной dr (рис. 4.18):

(4.36)

В уравнении (4.36) 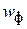заменим из (4.34) и его проинтегрируем:

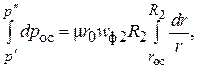
где 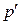– давление на внутренней границе слоя осадка (радиус 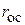) и 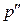– давление на внешней границе слоя осадка (радиус 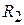). В результате получим:

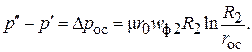(4.37)

В уравнении (4.37) 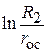заменим через известные параметры.
Найдем 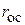из (4.33), а внутренний объем барабана центрифуги обозначим:

.

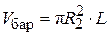Тогда получим:

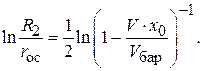(4.38)

Совместное решение уравнений (4.34), (4.37) и (4.38) относительно 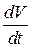с учетом сопротивления фильтровальной перегородки 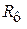дает:

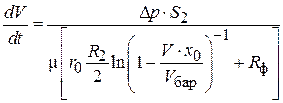, (4.39)

где 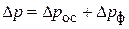, 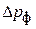– гидравлическое сопротивление фильтрующей перегородки.

Это и есть основное уравнение центробежного фильтрования.

Рассмотрим отдельные режимы фильтрования.

Режим 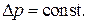Для этого случая Dp определяется по (4.32)
пр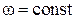и и .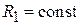

Решение уравнения (4.39) для этого случая имеется. Результаты громоздкие, поэтому их не приводим.

Режим 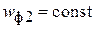можно поддержать при определенном законе изменения Dp. В конечном счете необходимо программировать изменения по времени w. Связь между Dp и w определяется по формулам (4.32), (4.39) с учетом уравнения неразрывности.