Кинематика опорно-двигательного аппарата (ОДА)

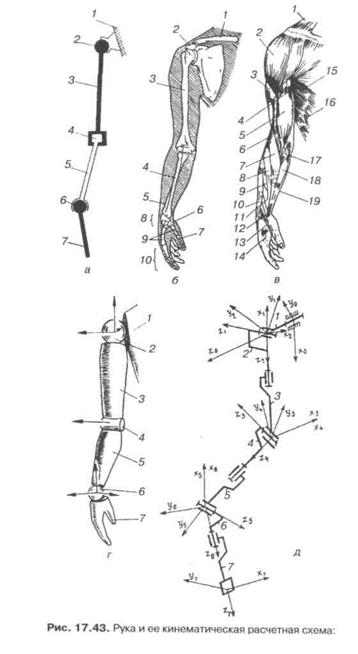
Рассмотрим кинематику руки человека (рис. 17,43). С точки зре­ния биомеханики, верхняя конечность может быть смоделирована многозвенным пространстввенным механизмом (рис. 17.43, д). Эта

система имеет семь степеней свободы. Плечевой сустав является шаровидным, т. е. имеет три степени свободы. На рис. 17.43, г он представлен эквивалентной схемой одноосных шарниров, оси вра­щения которых пересекаются в одной точке, а звенья 1, 2 имеют нулевую длину. Значит, положение седьмой системы координат в абсолютной, нулевой системе координат определяет формула:

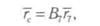
где — f_e — радиус-вектор точки С в абсолютной системе коорди­натных осей; г₇ — радиус-вектор точки С в седьмой системе коор­динат.

Анализируя угловые перемещения, скорости и ускорения звень­ев руки при исполнении различных целенаправленных движений типа «возьми—поставь» можно оценивать качественно и количе­ственно процесс реабилитации пациента или использование про­теза. Естественно, что при построении кинематической схемы и анализа движений нужно учитывать антропометрические дан­ные (табл. 17.8) и ограничения, налагаемые на движения в суста­вах (табл. 17.9).

На рис. 17.44 приведена схема двухзвенного механизма, кото­рым моделируется движение нижней конечности в фазе опоры. Та­кая схема позволяет определить перемещение мгновенного цент­ра вращения бедра. Считается, что плоское движение нижней

б — скелет руки: 1 — ключица, 2 — клювовидный отросток лопатки, 3 — плечевая кость, 4 — лучевая кость, 5 — локтевая кость, 6 — трапециевидная кость, 7 — про­ксимальная фаланга большого пальца, 8 — кости запястья, 9 — пястные кости, 10 — фаланги пальцев, д — система координат звеньев; а — кинематическая схе­ма: 1 — «плечевой» пояс, 2 — плечевая сферическая кинематическая пара, 3 — плечо, 4 — локтевая цилиндрическая пара, 5 — предплечье, 6— кистевая сфериче­ская пара, 7 — кисть, в — мышцы верхней конечности: 1 — трапециевидная, 2 — дельтовидная, 3 — трехглавая мышца плеча, 4 — клювоплечевая, 5 — двуглавая мышца плеча, 6 — плечевая, 7 — плечелучевая, 8 — длинный лучевой разгибатель запястья, 9 — короткий лучевой разгибатель запястья, 10 — разгибатель пальцев, ' 1 — длинная отводящая мышца большого пальца, 12 — короткий разгибатель боль­шого пальца, 13 — длинный разгибатель большого пальца, 14 — межкостная мышца, 15 — передняя зубчатая мышца, 16 — наружная косая мышца живота, 17 — круглый пронатор, 18 — лучевой сгибатель запястья, 19 — длинная ладонная мыш­ца, г — динамическая модель: 7 — туловище, 2 — плечевой шарнир, 3 — плечо, 4 — локтевой шарнир, 5 — предплечье, 6 — шарнир кисти, 7— кисть. Стрелки — компо­ненты мышечных моментов в суставах

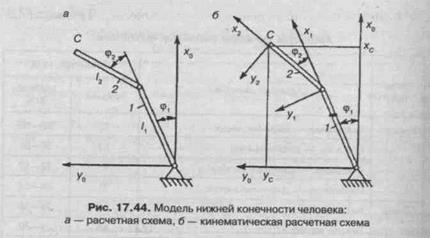
конечности происходит в сагиттальной плоскости вокруг оси го­леностопного сустава, остающейся неподвижной. За обобщенные координаты принимаются углы ф,(/) и <р₂(0. На рис. 17.44 показа­ны абсолютная и локальные оси координат. Положение точки С в абсолютной системе координатных осей находят по формуле:

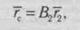
Здесь г₂ = (0,0, 0, 1 )^т; В₂ = Л Д, где Л. — матрица положения.

Обобщенные координаты задают как функцию времени по ре­зультатам экспериментальных наблюдений.

Решение обратной задачи кинематики представляют интерес для медицины и спорта. Формальная постановка обратной задачи кинематики требует решения уравнения:

По заданной матрице В. необходимо найти обобщенные коор­динаты g.. Матричное уравнение (17.1) эквивалентно шести ска­лярным уравнениям. При этом важно число степеней свободы ме­ханизма со, который модулирует органы человека.

1. Если со > 6, то число неизвестных обобщенных координат превышает число уравнений и множество решений оказывается бесконечным.

2. Если со < 6, то число неизвестных меньше числа уравнений. Задача будет иметь решение лишь при некоторых специальных по­ложениях механизма.

3. Если со = 6, то, приравняв наддиагональные элементы мат­риц 4-4, стоящих слева и справа в уравнении (17.1), можно получить систему из шести трансцендентных уравнений относительно обоб­щенных координат g Если это решение дает законы изменения обобщенных координат во времени g.(t), то, дифференцируя g.(t), можно найти обобщенные скорости g.(t) и обобщенные ускорения g.(t). Однако при этом погрешности расчета велики из-за необхо­димости использования методов численного дифференцирования.