Закон сохранения импульса

В подразделе (5.8) было введено понятие импульса произволь­ного тела и получено уравнение (5.19), описывающее изменение импульса под действием внешних сил. Так как изменение импуль­са обусловлено только внешними силами, то уравнение (5.19) удобно применять для описания взаимодействий нескольких тел. При этом взаимодействующие тела рассматривают как одно слож­ное тело (систему тел). Можно показать, что импульс сложного тела (системы тел) равен векторной сумме импульсов его частей:

Изменение импульса системы тел равно импульсу действую­щих на нее внешних сил.

Рассмотрим некоторые примеры, иллюстрирующие действие этого закона.

На рис. 9.10, а спортсменка стоит, опираясь правой ногой на скейтборд, а левой отталкивается от земли. Достигнутая при толчке скорость зависит от силы толчка и от времени, в течение которого эта сила действует.

На рис. 9.10, б изображен метатель копья. Скорость, которую приобретет копье данной массы, зависит от силы, приложенной рукой спортсмена и от времени, в течение которого она приложена.

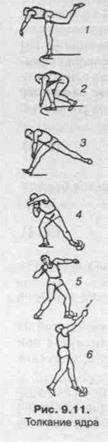
Поэтому перед броском копья спортсмен заносит руку далеко назад. Более детально подобный про­цесс разобран на примере спортсмена, толкаю­щего ядро, рис. 9.11.

Из равенства (9.14) вытекает одно важное для практического применения следствие, называе­мое законом сохранения импульса. Рассмотрим систему тел, на которую не действуют внешние силы. Такую систему называют замкнутой.

Система тел, которые взаимодействуют толь­ко между собой и не взаимодействуют с другими телами, называется замкнутой.

Векторная сумма импульсов тел, входя­щих в замкнутую систему, остается неизменной (сохраняется).

Иными словами, для любых двух моментов времени импульсы замкнутой системы одина­ковы:

исключений. Он абсолютно точно соблюдается и в макромире и в микромире.

Конечно, замкнутая система — это абстракция, так как прак­тически во всех случаях внешние силы есть. Однако для некоторых типов взаимодействий с очень малой длительностью наличием внешних сил можно пренебречь, так как при малом интервале дей­ствия импульс силы можно считать равным нулю:

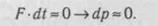
К процессам малой длительности относятся

• соударения движущихся тел

• распад тела на части (взрыв, выстрел, бросок).

Примеры

В боевиках часто присутствуют сцены, в которых после попа­дания пули человека отбрасывает по ходу выстрела. На экране это выглядит довольно эффектно. Проверим, возможно ли это? Пусть масса человек М =70 кг и он в момент попадания пули находится в состоянии покоя. Массу пули примем равной т = 9 г, а ее ско­рость v — 750 м/с. Если считать, что после попадания пули человек приходит в движение (в действительности этому может помешать сила трения между подошвами и полом), то для системы человек— пуля можно записать закон сохранения импульса: р, = р„. Перед попаданием пули человек не движется и в соответствии с (9.9) им­пульс системы р, = m-v +0. Будем считать, что пуля застревает в теле. Тогда конечный импульс системы р₂ = (М + т)-и, где и — скорость, которую получил человек при попадании пули. Подста­вив эти выражения в закон сохранения импульса, получим:

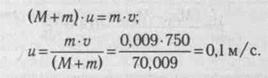
Полученный результат показывает, что ни о каком отлетании человека на несколько метров не может быть и речи (кстати, тело, брошенное вверх со скоростью 0,1м/с, поднимется на высоту всего 0,5 мм!).

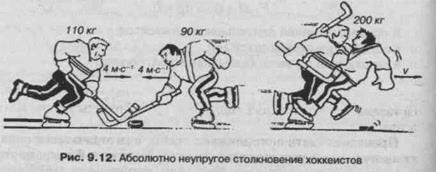
2) Столкновение хоккеистов.

Два хоккеиста массой М, и М₂ двигаются навстречу друг другу со скоростями, соответственно, v_v v₂ (рис. 9.12). Определить общую скорость их движения, считая столкновение абсолютно неупругим (при абсолютно неупругом ударе тела «сцепляются» и двигаются далее как одно целое).

Применим закон сохранения импульса к системе, состоящей из двух хоккеистов. Импульс системы перед столкновением р, =M_i-v_i — M₂v_r В этой формуле стоит знак «—» потому, что скорости и, и v₂ направлены навстречу друг другу. Направление скорости и, считается положительным, а направление скорости v₂ — отрица­тельным. После неупругого столкновения тела движутся с общей скоростью v и импульс системы р₂ = (М_{ + M₂)-v. Запишем закон сохранения импульса и найдем скорость v:

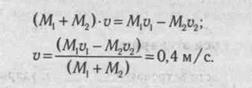
Направление скорости v определяется ее знаком.

Обратим внимание на одно важное обстоятельство: закон со­хранения импульса можно применять только к свободным телам. Если движение одного из тел ограничено внешними связями, то общий импульс сохраняться не будет.