Цель лекции: обобщить основные принципы разработки алгоритмов.

Рассматриваемые вопросы: методы декомпозиций (частных целей), подъема и отрабатывания назад, эвристики, рекурсия, поиск с возвратом.

При выборе алгоритма следует изучить существующие алгоритмы и структуры данных. Подумайте, какой объем данных может обработать программа. Если задача предполагает скромные размеры данных, то выбирайте простые технологии; если количество данных может расти, то исключите решения, плохо приспосабливающиеся к этому росту. Там, где возможно, используйте библиотеку или специальные средства языка. Если ничего готового нет, то напишите короткую, простую, понятную реализацию. Попробуйте ее в действии. Если измерения показывают, что она слишком медленная, только тогда вам стоит перейти к более продвинутым технологиям.

Хотя есть много структур данных, часть которых просто необходима для приемлемой производительности в определенных условиях, большинство программ основано на массивах, списках, деревьях и хэш-таблицах. Каждая из этих структур поддерживает набор операций-примитивов, обычно включающий в себя: создание нового элемента, поиск элемента, добавление элемента куда-либо, возможно, удаление элемента и применение некоторой операции ко всем элементам.

У каждой операции есть ожидаемое время выполнения, которое часто определяет, насколько выбранный тип данных или его реализация подходит для конкретного приложения. Массивы предоставляют доступ к элементам за константное время, но зато плохо изменяют свои размер; Списки хорошо приспособлены для вставки и удаления, но случайный доступ к элементам происходит лишь за линейное время. Деревья и хэш-таблицы предоставляют разумный компромисс: быстрый доступ к заданным элементам в сочетании с легкой расширяемостью, пока в их структуре соблюдается определенный баланс.

Есть еще множество изощренных структур данных для специальных задач, однако этот базовый набор вполне достаточен для написания подавляющего большинства программ

Рассмотрим несколько фундаментальных методов разработки алгоритмов и решения задач. Ключевым подходом в алгоритмизации является сведение задачи к подзадачам. Это естественно, так как предстоит превратить один шаг в последовательность элементарных шагов. Само это преобразование также может состоять из нескольких этапов, на которых единственный шаг разбивается на несколько более простых, но еще не элементарных. Эти более простые шаги соответствуют частным задачам (подзадачам), совокупное решение которых приводит к решению исходной задачи. Иерархию задач можно изобразить в виде дерева.

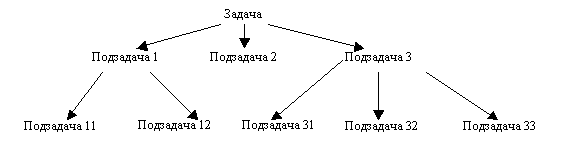
Иерархия задач

Различные методы разработки алгоритмов отличаются тем, на какие подзадачи производится разбиение и как эти подзадачи соотносятся между собой. Хотя нет общепринятой классификации методов разработки алгоритмов, тем не менее, некоторые общие соображения на этот счет могут быть высказаны.

Любая задача может быть сформулирована как функция преобразования исходных данных в выходные данные, f(X)=Y. Как исходные данные, так и функция могут быть достаточно сложными.

Разбивая задачу на подзадачи, можно:

• разбивать исходные и выходные данные на части или упрощать их; под разбиением понимаем разделение структуры данных на части, например, разделение вектора из десяти компонент на два вектора по пять компонент или разделение текста на предложения; под упрощением понимаем такие ситуации, когда, например X - число и его нельзя разбить на части, но его можно разложить, скажем, в сумму X = X1 + X2, так, что результаты f(X1), f(X2) отыскиваются проще, чем f(X);
• производить декомпозицию функции, т. е. превращать ее в суперпозицию более простых, f(Х) = g(h(s(X))) или f(Х) = g(X, h(X), s(X)).

При разработке алгоритма может систематически использоваться первый подход, систематически использоваться второй подход или могут совместно использоваться оба подхода.

1. Методы декомпозиций (частных целей), подъема и отрабатывания назад, эвристики

Метод, называемый также методом «разделяй и властвуй», или методом разбиения, связан со сведением трудной задачи к последовательности более простых задач. Он предполагает такую декомпозицию (разбиение) задачи размера п на более мелкие задачи, что на основе решений этих более мелких задач можно легко получить решение исходной задачи. Конечно, мы надеемся на то, что более простые задачи легче поддаются обработке, чем первоначальная задача, а также на то, что решение первоначальной задачи может быть получено из решений этих более простых задач. Такая процедура называется методом частных целей.

Важный частный случай:разложение задачи в последовательность однородных подзадач (итерация)

Второй метод разработки алгоритмов известен как метод подъема. Алгоритм подъема начинается с принятия начального предположения или вычисления начального решения задачи. Затем начинается насколько возможно быстрое движение «вверх» от начального решения по направлению к лучшим решениям. Когда алгоритм достигает такую точку, из которой больше невозможно двигаться наверх, алгоритм останавливается. К сожалению, мы не можем всегда гарантировать, что окончательное решение, полученное с помощью алгоритма подъема, будет оптимальным. Этот «дефект» часто ограничивает применение метода подъема.

Третий метод, рассматриваемый в этом разделе, известен как отрабатывание назад, т. е. начинаем с цели или решения и движемся обратно по направлению к начальной постановке задачи. Затем, если эти действия обратимы, движемся обратно от постановки задачи к решению.

Эвристический алгоритм, или эвристика, определяется как алгоритм со следующими свойствами:

1. Он обычно находит хорошие, хотя не обязательно оптимальные решения.

2. Его можно быстрее и проще реализовать, чем любой известный точный алгоритм (т. е. тот, который гарантирует оптимальное решение).

Понятия «хороший» и «обычно» в свойстве 1 меняются от задачи к задаче. Например, если для решения задачи все известные точные алгоритмы требуют нескольких лет машинного времени, то мы можем охотно принять любое нетривиальное приближенное решение, которое может быть получено за разумное время. С другой стороны, имея быстрое, близкое к оптимальному решение, мы можем стремиться все же к точному решению.

Хотя не существует универсальной структуры, которой можно описать эвристические алгоритмы, многие из них основываются или на методе частных целей, или на методе подъема. Один общий подход к построению эвристических алгоритмов заключается в перечислении всех требований к точному решению и разделении требований на два класса, например:

1. Те, которые легко удовлетворить.

2. Те, которые не так легко удовлетворить.

1. Те, которые должны быть удовлетворены.

2. Те, по отношению к которым мы могли бы пойти на компромисс.

Тогда цель построения алгоритма - создать алгоритм, гарантирующий выполнение требований 1-го класса, но не обязательрю 2-го. Это не означает, что для удовлетворения требований 2-го класса не делается никаких попыток, это просто означает, что не может быть дано никаких гарантий, что оии будут удовлетворены.