ЛЕКЦИЯ 9. ЛЕС, ДЕРЕВО. РЕАЛИЗАЦИЯ В ДИНАМИЧЕСКОЙ ПАМЯТИ. ОБХОДЫ ДЕРЕВА.

Цели и задачи лекции:

Ознакомление с основными понятиями и определениями древовидных структур.

Основные рассматриваемые вопросы.

Определение дерева, леса, бинарного дерева. Графическое и текстовое (скобочное) представление леса. Спецификация дерева, леса, бинарного дерева: базовые функции и аксиомы. Естественное соответствие бинарного дерева и леса.

Дерево – конечное множество Т, состоящее из одного или более узлов, таких, что

а) имеется один специально обозначенный узел, называемый корнем данного дерева;

б) остальные узлы (исключая корень) содержатся в m ³ 0 попарно не пересекающихся множествах Т1, Т2, ..., Тm, каждое из которых, в свою очередь, является деревом. Деревья Т1, Т2, ..., Тm называются поддеревьями данного дерева.

Если в определении дерева существен порядок перечисления поддеревьев Т1, Т2, ..., Тm, то дерево называют упорядоченным и говорят о «первом» (Т1), «втором» (Т2) и т. д. поддеревьях данного корня. Далее будем считать, что все рассматриваемые деревья являются упорядоченными, если явно не оговорено противное.

Например, два упорядоченных дерева на рисунке различаются.

Лес – это множество (обычно упорядоченное), состоящее из некоторого (быть может, равного нулю) числа непересекающихся деревьев. Используя понятие леса, пункт б в определении дерева можно было бы сформулировать так: узлы дерева, за исключением корня, образуют лес.

По определению, корень дерева находится на уровне 0, а все вершины дерева, непосредственно связанные с вершиной уровня i, находятся на уровне i+1. Вершина x уровня i, непосредственно связанная с вершиной y уровня i+1, называется непосредственным предком (или родителем) вершины y. Такая вершина y соответственно называется непосредственным потомком (или сыном) вершины x. Вершина без непосредственных потомков называется листовой (или терминальной), нелистовые вершины называются внутренними. Под степенью внутренней вершины понимается число ее непосредственных потомков. Если все вершины имеют одну и ту же степень, то она полагается степенью дерева. Число вершин (или ветвей), которые нужно пройти от корня к вершине x, называется длиной пути к вершине x. Высотой (или глубиной) дерева будем называть максимальную длину пути

Традиционно дерево изображают графически, например так, как на рис. 3.1.

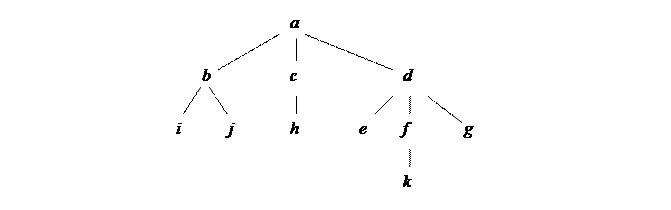Рис.. Графическое изображение дерева

Другой вид текстового (и принципиально одномерного) представления дерева - это так называемая скобочная запись Определим скобочное представление дерева и леса:

< лес > ::= пусто | < дерево > < лес >,

< дерево > ::= ( < корень > < лес > ).

В скобочном представлении дерево, изображенное на рис. 1, запишется как

(a (b (i) (j)) (c (h)) (d (e) (f (k)) (g))).

По величине степени дерева часто различают два типа деревьев:

- двоичные - степень дерева не более двух;

- сильноветвящиеся - степень дерева произвольная.

Списочное представление деревьев произвольной степени основано на элементах, соответствующих вершинам дерева. Каждый элемент имеет поле данных и два поля указателей: указатель на начало списка потомков вершины и указатель на следующий элемент в списке потомков текущего уровня. При таком способе представления дерева обязательно следует сохранять указатель на вершину, являющуюся корнем дерева:

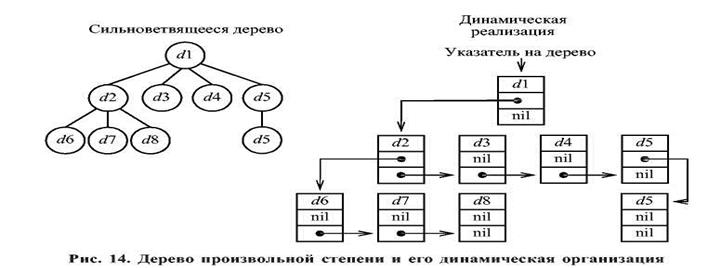
Type

Ptree=^ Ttree;

= record

Data: TypeElement; {поле данных}

ChiId1, ChiId2, ChiId3: PTree; {указатели на потомков }

end;

Двоичные деревья. В программировании особое значение имеют упорядоченные двоичные (бинарные) деревья. В каждом таком дереве естественно определяются левое и правое поддеревья. Удобно дать следующее формальное определение. Бинарное дерево - конечное множество узлов, которое либо пусто, либо состоит из корня и двух непересекающихся бинарных деревьев, называемых правым поддеревом и левым поддеревом.